आर में सामान्य सीडीएफ का उपयोग कैसे करें (उदाहरण के साथ)

आप आर में सामान्य सीडीएफ (संचयी वितरण फ़ंक्शन) के साथ काम करने के लिए निम्नलिखित विधियों का उपयोग कर सकते हैं:

विधि 1: सामान्य सीडीएफ संभावनाओं की गणना करें

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

विधि 2: सामान्य सीडीएफ प्लॉट करें

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ")

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में इन विधियों का उपयोग कैसे करें।

उदाहरण 1: सामान्य सीडीएफ संभावनाओं की गणना करें

निम्नलिखित कोड दिखाता है कि इस संभावना की गणना कैसे करें कि एक यादृच्छिक चर एक मानक सामान्य वितरण में 1.96 से कम मान लेता है:

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

[1] 0.9750021

मानक सामान्य वितरण में एक यादृच्छिक चर का मान 1.96 से कम होने की प्रायिकता 0.975 है।

हम लोअर.टेल तर्क का उपयोग करके यह संभावना भी पा सकते हैं कि एक यादृच्छिक चर 1.96 से अधिक मान लेता है:

 #calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

[1] 0.0249979

और हम इस संभावना को खोजने के लिए निम्नलिखित सिंटैक्स का उपयोग कर सकते हैं कि एक यादृच्छिक चर एक मानक सामान्य वितरण में दो मानों के बीच एक मान लेता है:

 #calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

मानक सामान्य वितरण में एक यादृच्छिक चर का मान -1.96 और 1.96 के बीच होने की संभावना 0.95 है।

उदाहरण 2: सामान्य सीडीएफ प्लॉट करना

निम्नलिखित कोड दिखाता है कि सामान्य सीडीएफ कैसे प्लॉट करें:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ") 

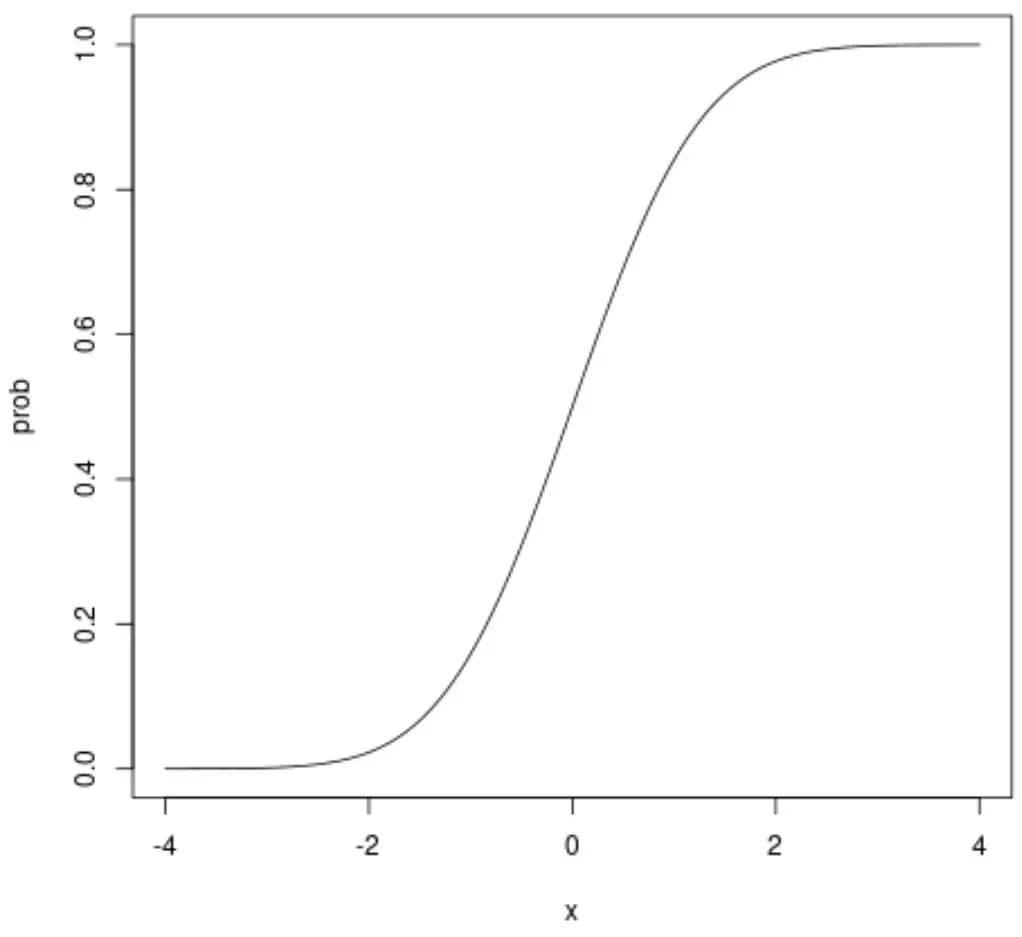
एक्स-अक्ष एक यादृच्छिक चर के मान दिखाता है जो मानक सामान्य वितरण का पालन करता है और वाई-अक्ष संभावना दिखाता है कि एक यादृच्छिक चर एक्स-अक्ष पर दिखाए गए मान से कम मान लेता है।

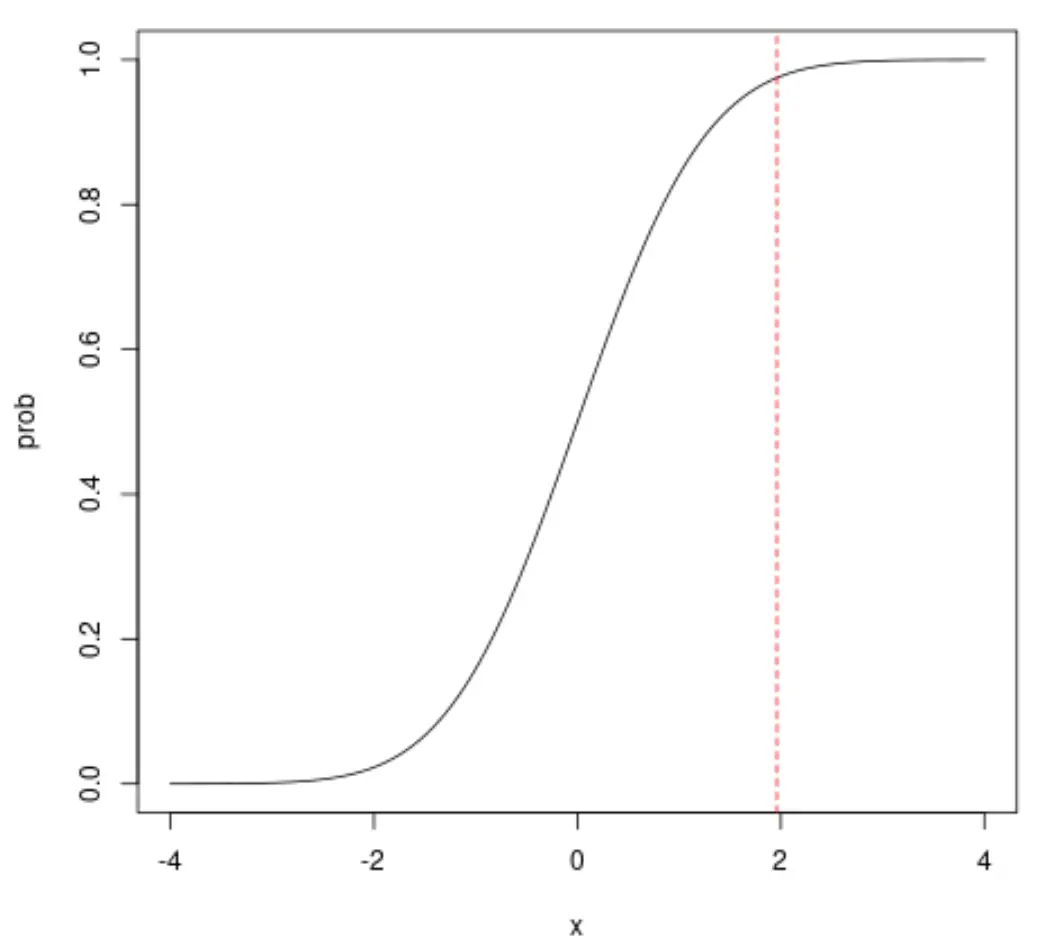
उदाहरण के लिए, यदि हम x = 1.96 को देखें, तो हम देखेंगे कि x के 1.96 से कम होने की संचयी संभावना लगभग 0.975 है:

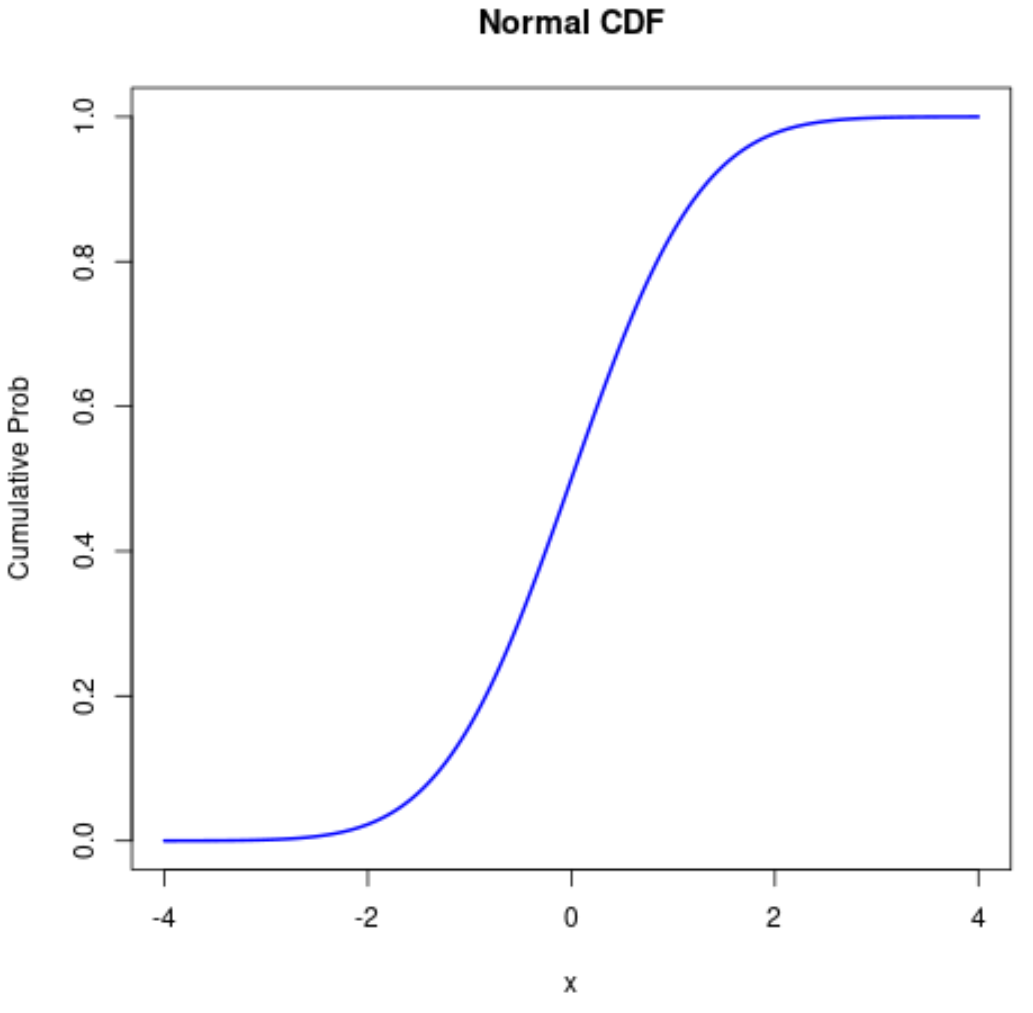
ध्यान दें कि आप सामान्य सीडीएफ प्लॉट के सौंदर्यशास्त्र को भी बदल सकते हैं:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ') 

संबंधित: R में seq फ़ंक्शन का उपयोग कैसे करें

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्य ऑपरेशन कैसे करें:

आर में सामान्य वितरण कैसे प्लॉट करें
R में Z स्कोर की गणना कैसे करें
R में dnorm, pnorm, qnorm और rnorm के लिए एक गाइड