आवृत्ति तालिका

यह आलेख बताता है कि सांख्यिकी में आवृत्ति तालिका क्या है। इस प्रकार, आप जानेंगे कि आवृत्ति तालिका कैसे बनाई जाती है, आवृत्ति तालिकाओं के उदाहरण और, इसके अलावा, आप हल किए गए अभ्यासों के साथ अभ्यास करने में सक्षम होंगे।

आवृत्ति तालिका क्या है?

सांख्यिकी में, आवृत्ति तालिका एक तालिका होती है जिसमें डेटा का एक सेट विभिन्न श्रेणियों में व्यवस्थित होता है और सभी प्रकार की नमूना आवृत्तियों को प्रदर्शित किया जाता है।

विशेष रूप से, एक आवृत्ति तालिका में पूर्ण आवृत्ति, संचयी पूर्ण आवृत्ति, सापेक्ष आवृत्ति और संचयी सापेक्ष आवृत्ति शामिल होती है।

आवृत्ति तालिकाओं की एक विशेषता यह है कि इनका उपयोग मात्रात्मक चर और गुणात्मक चर के सांख्यिकीय नमूने को सारांशित करने के लिए किया जाता है।

फ़्रीक्वेंसी टेबल कैसे बनाएं

आवृत्ति तालिका बनाने के चरण हैं:

1. डेटा को विभिन्न श्रेणियों में व्यवस्थित करें और एक तालिका बनाएं जिसमें प्रत्येक पंक्ति एक श्रेणी से मेल खाती हो।
2. आवृत्ति तालिका के दूसरे कॉलम में प्रत्येक श्रेणी की पूर्ण आवृत्ति की गणना करें ।
3. आवृत्ति तालिका के तीसरे कॉलम में प्रत्येक श्रेणी की संचयी निरपेक्ष आवृत्ति की गणना करें ।
4. आवृत्ति तालिका के चौथे स्तंभ में प्रत्येक श्रेणी की सापेक्ष आवृत्ति की गणना करें ।
5. आवृत्ति तालिका के पांचवें कॉलम में प्रत्येक श्रेणी की संचयी सापेक्ष आवृत्ति की गणना करें ।
6. वैकल्पिक रूप से, दो कॉलम जोड़े जा सकते हैं जिनमें सापेक्ष आवृत्ति और संचयी सापेक्ष आवृत्ति की गणना प्रतिशत के रूप में की जाती है, इसके लिए आपको बस दोनों कॉलमों को 100 से गुणा करना होगा।

ध्यान रखें कि यदि चर निरंतर है, तो आवृत्ति तालिका में श्रेणियां संख्याओं के बजाय अंतराल होंगी। ताकि आप देख सकें कि आवृत्ति तालिका कैसे बनाई जाती है, यहां चरण दर चरण हल किए गए दो उदाहरण दिए गए हैं: पहले में, डेटा को अलग किया जाता है और दूसरे में, डेटा को अंतरालों में समूहीकृत किया जाता है।

आवृत्ति तालिका का उदाहरण

आवृत्ति तालिका की परिभाषा और इसके निर्माण के सिद्धांत पर विचार करते हुए, इस खंड में एक उदाहरण को चरण दर चरण हल किया गया है।

• 30 छात्रों की एक कक्षा में सांख्यिकी विषय में प्राप्त ग्रेड इस प्रकार हैं। डेटासेट की एक आवृत्ति तालिका बनाएं।

चूँकि सभी संख्याएँ केवल पूर्णांक हो सकती हैं, यह एक असतत चर है। इसलिए डेटा को अंतरालों में समूहित करना आवश्यक नहीं है।

इसलिए हमें एक तालिका बनाने की आवश्यकता है जिसमें प्रत्येक भिन्न मान एक पंक्ति होगी। इसके अलावा, हमें प्रत्येक मान की पूर्ण आवृत्ति ज्ञात करने की आवश्यकता है, ऐसा करने के लिए, बस डेटा नमूने में मान प्रकट होने की संख्या की गणना करें।

ध्यान दें कि सभी निरपेक्ष आवृत्तियों का योग डेटा की कुल संख्या के बराबर है। यदि इस नियम का सम्मान नहीं किया जाता है, तो इसका मतलब है कि आप कुछ जानकारी प्रदान करना भूल गए हैं।

अब जब हम निरपेक्ष आवृत्ति जानते हैं, तो हमें संचयी निरपेक्ष आवृत्ति की गणना करने की आवश्यकता है। इस गणना के लिए हमारे पास दो विकल्प हैं: या तो हम मूल्य की पूर्ण आवृत्ति और सबसे छोटे मूल्यों की सभी पूर्ण आवृत्तियों को जोड़ दें, या इसके विपरीत, हम मूल्य की पूर्ण आवृत्ति और पिछले मूल्य की संचयी पूर्ण आवृत्ति को जोड़ दें।

अंतिम मान की संचयी निरपेक्ष आवृत्ति हमेशा डेटा की कुल संख्या से मेल खाती है, आप यह सत्यापित करने के लिए इस ट्रिक का उपयोग कर सकते हैं कि गणना सही है।

इसके बाद, हमें सापेक्ष आवृत्ति निर्धारित करने की आवश्यकता है, जिसकी गणना पूर्ण आवृत्ति को डेटा बिंदुओं की कुल संख्या (30) से विभाजित करके की जाती है:

ध्यान रखें कि सभी सापेक्ष आवृत्तियों का योग हमेशा 1 के बराबर होता है, अन्यथा इसका मतलब है कि आवृत्ति तालिका में कुछ गणनाएँ गलत हैं।

अंततः, यह संचित सापेक्ष आवृत्ति को निकालने के लिए पर्याप्त है। ऐसा करने के लिए, आपको प्रश्न में मूल्य की सापेक्ष आवृत्ति और पिछली सभी सापेक्ष आवृत्तियों को जोड़ना होगा या, जो एक ही चीज़ के बराबर है, पिछली संचित सापेक्ष आवृत्ति:

संक्षेप में, समस्याग्रस्त डेटा की सभी आवृत्तियों के साथ आवृत्ति तालिका इस प्रकार है:

समूहीकृत डेटा के लिए आवृत्ति तालिका

अंतरालों में समूहित डेटा के लिए एक आवृत्ति तालिका बनाने के लिए, एकमात्र अंतर यह है कि डेटा सेट को पहले अलग-अलग अंतरालों में समूहीकृत किया जाना चाहिए, लेकिन बाकी गणनाएं आवृत्ति तालिका की तरह ही की जाती हैं। डेटा को समूहीकृत किए बिना आवृत्ति।

उदाहरण के तौर पर, समूहीकृत डेटा के लिए आवृत्ति तालिका बनाने से संबंधित एक समस्या का समाधान नीचे दिया गया है।

• 20 लोगों की ऊंचाई मापी गई और नीचे दिए गए परिणाम प्राप्त किए गए। डेटा को अंतरालों में अलग करते हुए एक आवृत्ति तालिका तैयार करें।

इस नमूने में डेटा एक सतत वितरण का अनुसरण करता है, क्योंकि संख्याएँ दशमलव हो सकती हैं और इसलिए कोई भी मान ले सकती हैं। इसलिए, हम डेटा को अंतरालों में समूहीकृत करते हुए आवृत्ति तालिका बनाएंगे।

हालाँकि किसी नमूने के अंतराल बनाने के लिए कई गणितीय नियम हैं, इस मामले में हम केवल 10 दसवें की चौड़ाई के साथ अंतराल बनाएंगे।

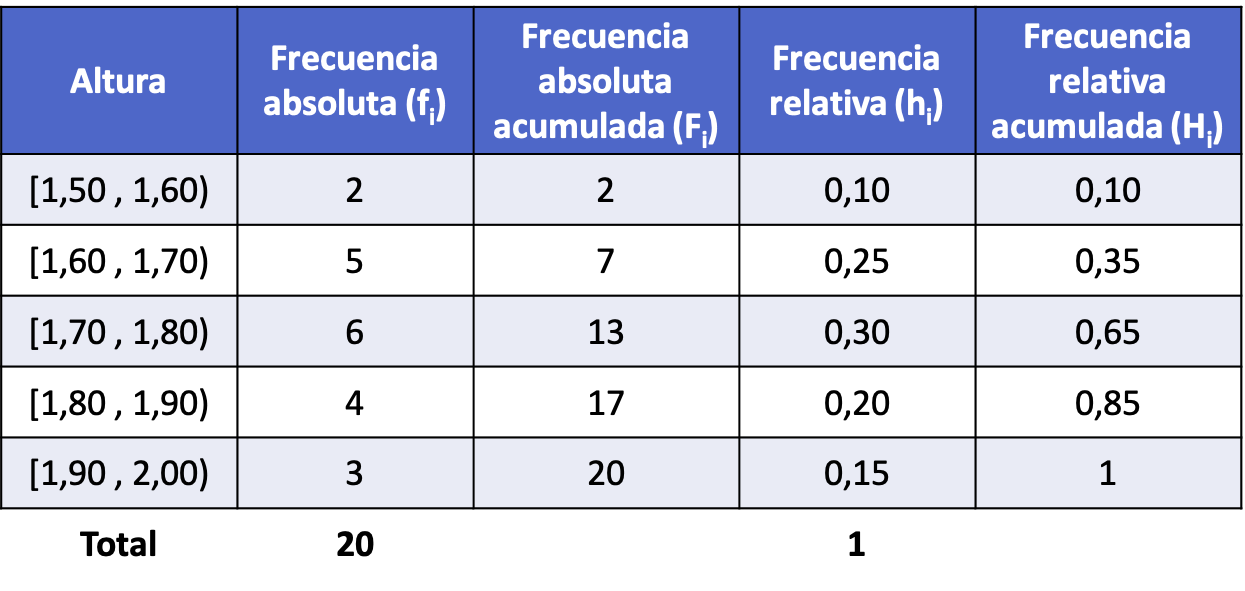
इसलिए, प्रत्येक अंतराल के लिए सभी प्रकार की आवृत्तियों की गणना करने के बाद (प्रक्रिया पिछले उदाहरण के समान है), अंतराल में समूहीकृत डेटा के साथ आवृत्ति तालिका इस तरह दिखती है:

हल की गई आवृत्ति तालिका अभ्यास

अभ्यास 1

हमने 20 लोगों से पूछा कि वे प्रति माह कितनी बार सिनेमा जाते हैं और परिणाम यहां हैं:

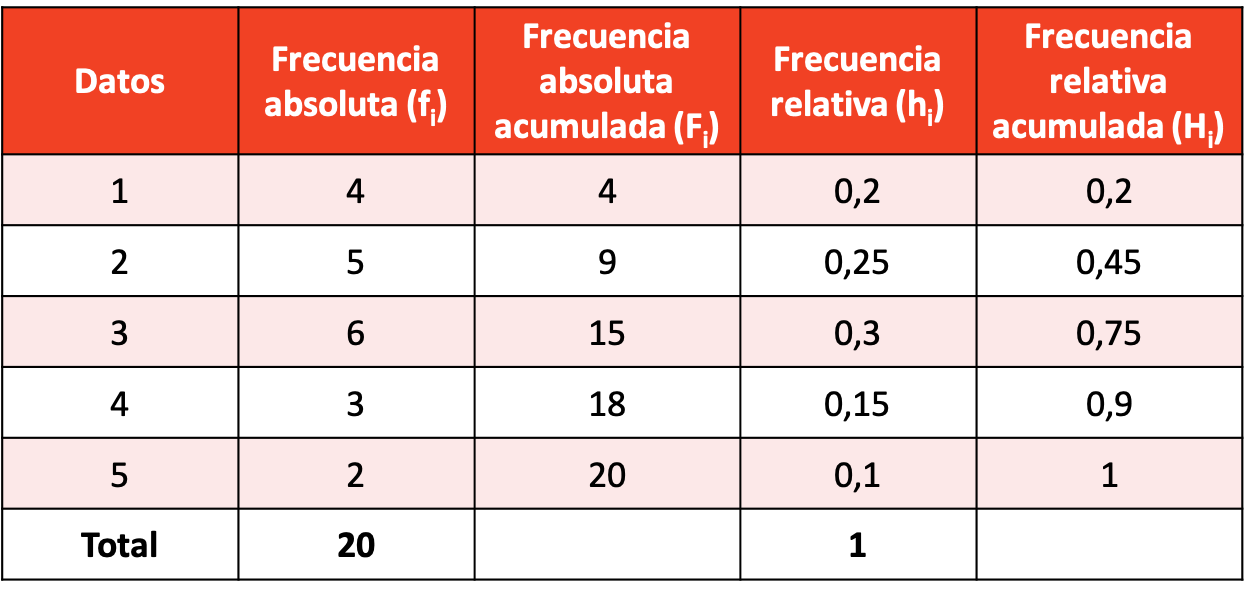
परिणामी नमूना डेटा के साथ एक आवृत्ति तालिका बनाएं।

सभी प्रकार की आवृत्तियों की गणना के साथ आवृत्ति तालिका इस प्रकार है:

व्यायाम 2

हम 36 कर्मचारियों वाली कंपनी में श्रमिकों के वजन पर एक सांख्यिकीय अध्ययन करना चाहेंगे। यहां श्रमिकों का वजन किलोग्राम में व्यक्त किया गया है:

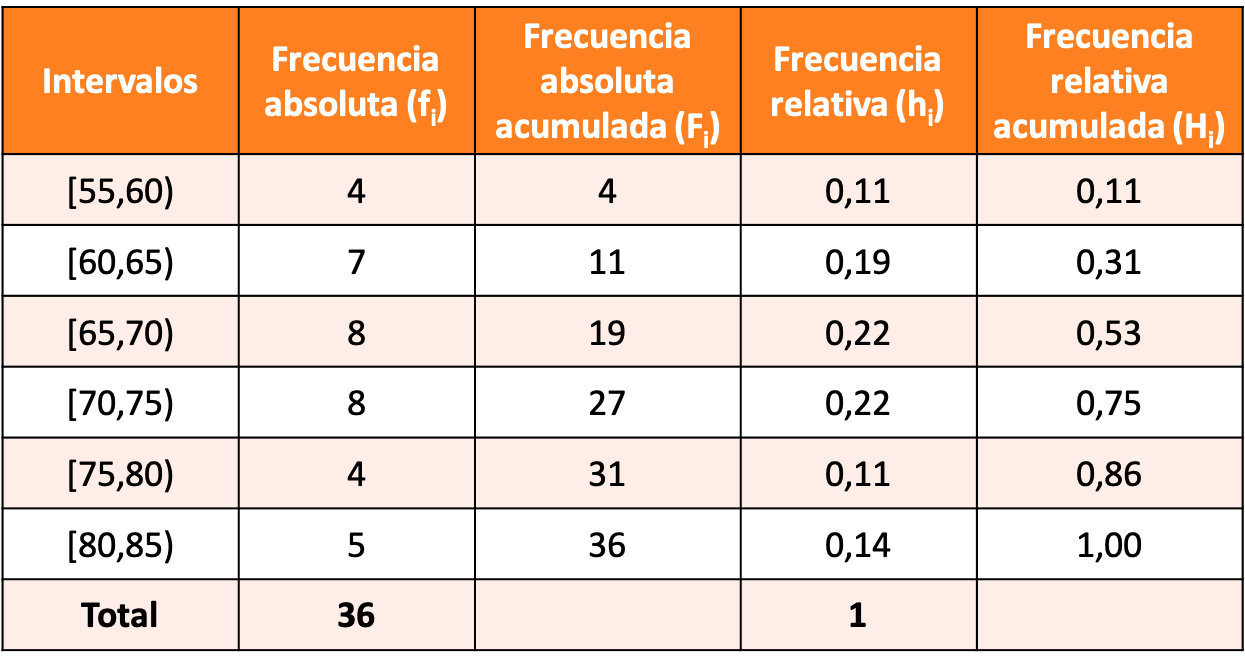
5 इकाइयों के अंतराल बनाकर और पहला अंतराल [55,60) बनाकर डेटा को समूहीकृत करके एक आवृत्ति तालिका बनाएं।

अभ्यास का समाधान निम्नलिखित आवृत्ति तालिका है: