इंट्राक्लास सहसंबंध गुणांक: परिभाषा + उदाहरण

एक इंट्राक्लास सहसंबंध गुणांक (आईसीसी) का उपयोग उन अध्ययनों में स्कोर की विश्वसनीयता को मापने के लिए किया जाता है जहां दो या दो से अधिक मूल्यांकनकर्ता होते हैं।

ICC का मान 0 से 1 तक हो सकता है, जिसमें 0 मूल्यांकनकर्ताओं के बीच कोई विश्वसनीयता नहीं होने का संकेत देता है और 1 मूल्यांकनकर्ताओं के बीच पूर्ण विश्वसनीयता का संकेत देता है।

सीधे शब्दों में कहें तो, ICC का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या वस्तुओं (या विषयों) को विभिन्न मूल्यांकनकर्ताओं द्वारा विश्वसनीय रूप से रेट किया जा सकता है।

ICC के कई अलग-अलग संस्करण हैं जिनकी गणना निम्नलिखित तीन कारकों के आधार पर की जा सकती है:

• मॉडल: एक-तरफ़ा यादृच्छिक प्रभाव, दो-तरफ़ा यादृच्छिक प्रभाव, या दो-तरफ़ा मिश्रित प्रभाव
• रिश्ते का प्रकार: स्थिरता या पूर्ण सहमति
• इकाई: एकल मूल्यांकनकर्ता या मूल्यांकनकर्ताओं का औसत

यहां तीन अलग-अलग मॉडलों का संक्षिप्त विवरण दिया गया है:

1. एक-तरफ़ा यादृच्छिक प्रभाव मॉडल: यह मॉडल मानता है कि प्रत्येक विषय का मूल्यांकन यादृच्छिक रूप से चयनित मूल्यांकनकर्ताओं के एक अलग समूह द्वारा किया जाता है। इस मॉडल के साथ, मूल्यांकनकर्ताओं को यादृच्छिक प्रभावों का स्रोत माना जाता है। इस मॉडल का व्यवहार में शायद ही कभी उपयोग किया जाता है क्योंकि आमतौर पर प्रत्येक विषय का मूल्यांकन करने के लिए मूल्यांकनकर्ताओं के एक ही समूह का उपयोग किया जाता है।

2. दो-तरफा यादृच्छिक प्रभाव मॉडल: यह मॉडल मानता है कि मूल्यांकनकर्ताओं के एक समूह को आबादी से यादृच्छिक रूप से चुना जाता है और फिर विषयों को रेट करने के लिए उपयोग किया जाता है। इस मॉडल का उपयोग करते हुए, मूल्यांकनकर्ताओं और विषयों को यादृच्छिक प्रभावों का स्रोत माना जाता है। इस मॉडल का उपयोग अक्सर तब किया जाता है जब हम मूल्यांकनकर्ताओं के लिए अपने परिणामों को अध्ययन में उपयोग किए गए परिणामों के समान सामान्यीकृत करना चाहते हैं।

3. दो-तरफ़ा मिश्रित प्रभाव मॉडल: यह मॉडल यह भी मानता है कि मूल्यांकनकर्ताओं के एक समूह को आबादी से यादृच्छिक रूप से चुना जाता है और फिर विषयों को रेट करने के लिए उपयोग किया जाता है। हालाँकि, यह मॉडल मानता है कि हमारे द्वारा चुने गए मूल्यांकनकर्ताओं का समूह ही एकमात्र रुचिकर मूल्यांकनकर्ता है, जिसका अर्थ है कि हम अपने परिणामों को अन्य मूल्यांकनकर्ताओं के लिए सामान्यीकृत नहीं करना चाहते हैं, जो अध्ययन में उपयोग किए गए मूल्यांकनकर्ताओं के समान विशेषताओं को साझा कर सकते हैं।

यहां उन दो अलग-अलग प्रकार के रिश्तों का संक्षिप्त विवरण दिया गया है जिन्हें हम मापना चाहते हैं:

1. संगति: हम न्यायाधीशों की रेटिंग के बीच व्यवस्थित अंतर में रुचि रखते हैं (उदाहरण के लिए, क्या न्यायाधीशों ने समान विषयों को निम्न और उच्च के रूप में रेटिंग दी है?)

2. पूर्ण सहमति: हम न्यायाधीशों के अंकों के बीच पूर्ण अंतर में रुचि रखते हैं (उदाहरण के लिए, न्यायाधीश ए और न्यायाधीश बी के अंकों के बीच पूर्ण अंतर क्या है?)

यहां उन दो अलग-अलग इकाइयों का संक्षिप्त विवरण दिया गया है जिनमें हमारी रुचि हो सकती है:

1. एकल समीक्षक: हम माप के आधार के रूप में केवल एक समीक्षक की रेटिंग का उपयोग करना चाहते हैं।

2. रेटर औसत: हम माप के आधार के रूप में सभी न्यायाधीशों के अंकों के औसत का उपयोग करना चाहते हैं।

नोट: यदि आप दो मूल्यांकनकर्ताओं के बीच समझौते के स्तर को मापना चाहते हैं जो द्विभाजित परिणाम पर प्रत्येक आइटम को चूक जाते हैं, तो आपको इसके बजाय कोहेन के कप्पा का उपयोग करना चाहिए।

इंट्राक्लास सहसंबंध गुणांक की व्याख्या कैसे करें

कू और ली के अनुसार, इंट्राक्लास सहसंबंध गुणांक के मूल्य की व्याख्या कैसे करें:

• 0.50 से कम: खराब विश्वसनीयता
• 0.5 और 0.75 के बीच: मध्यम विश्वसनीयता
• 0.75 और 0.9 के बीच: अच्छी विश्वसनीयता
• 0.9 से अधिक: उत्कृष्ट विश्वसनीयता

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में इंट्राक्लास सहसंबंध गुणांक की गणना कैसे करें।

उदाहरण: इंट्राक्लास सहसंबंध गुणांक की गणना

मान लीजिए कि चार अलग-अलग न्यायाधीशों को 10 अलग-अलग कॉलेज प्रवेश परीक्षाओं की गुणवत्ता का मूल्यांकन करने के लिए कहा जाता है। परिणाम नीचे दर्शाए गए है:

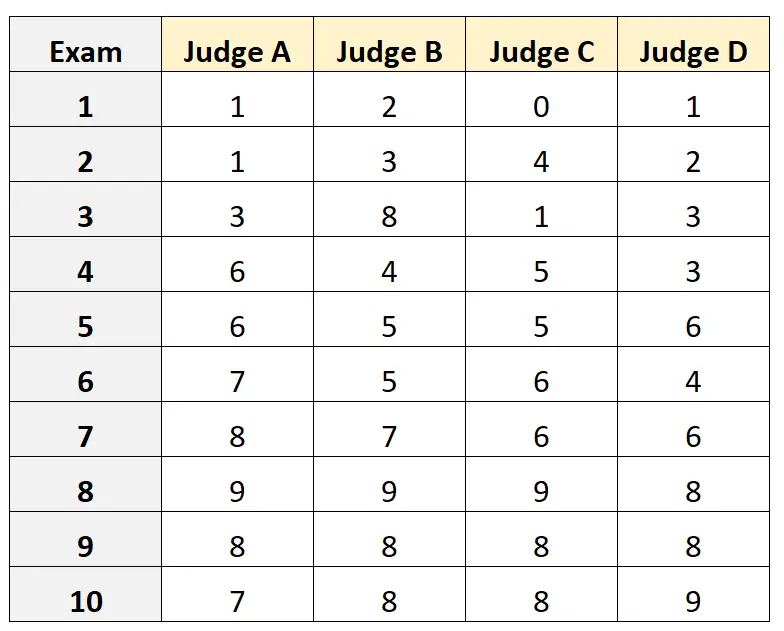
मान लीजिए कि चार न्यायाधीशों को प्रवेश परीक्षा के लिए योग्य न्यायाधीशों की आबादी से यादृच्छिक रूप से चुना गया था और हम न्यायाधीशों के बीच पूर्ण समझौते को मापना चाहते थे और हम अपने माप के आधार के रूप में केवल एक मूल्यांकनकर्ता के परिप्रेक्ष्य से स्कोर का उपयोग करना चाहते थे।

हम दो-तरफा यादृच्छिक प्रभाव मॉडल को फिट करने के लिए आर में निम्नलिखित कोड का उपयोग कर सकते हैं, मूल्यांकनकर्ताओं के बीच संबंध के रूप में पूर्ण समझौते का उपयोग कर सकते हैं और एकल इकाई को रुचि की इकाई के रूप में उपयोग कर सकते हैं:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

इंट्राक्लास सहसंबंध गुणांक (आईसीसी) 0.782 पाया गया।

आईसीसी की व्याख्या के लिए सामान्य नियमों के आधार पर, हम यह निष्कर्ष निकालेंगे कि 0.782 का आईसीसी इंगित करता है कि परीक्षाओं को विभिन्न मूल्यांकनकर्ताओं द्वारा “अच्छी” विश्वसनीयता के साथ स्कोर किया जा सकता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल विभिन्न सांख्यिकीय सॉफ़्टवेयर में आईसीसी की गणना करने के तरीके पर विस्तृत विवरण प्रदान करते हैं:

एक्सेल में इंट्राक्लास सहसंबंध गुणांक की गणना कैसे करें
आर में इंट्राक्लास सहसंबंध गुणांक की गणना कैसे करें
पायथन में इंट्राक्लास सहसंबंध गुणांक की गणना कैसे करें