Ti-84 कैलकुलेटर पर invnorm का उपयोग कैसे करें (उदाहरण के साथ)

आप सामान्य वितरण से जुड़े z महत्वपूर्ण मानों को खोजने के लिए TI-84 कैलकुलेटर पर invNorm() फ़ंक्शन का उपयोग कर सकते हैं।

यह फ़ंक्शन निम्नलिखित सिंटैक्स का उपयोग करता है:

invNorm(संभावना, μ, σ)

सोना:

• संभाव्यता: महत्व का स्तर
• μ: जनसंख्या औसत
• σ: जनसंख्या मानक विचलन

आप इस फ़ंक्शन को TI-84 कैलकुलेटर पर 2 दबाकर और फिर VARS दबाकर एक्सेस कर सकते हैं। यह आपको DISTR स्क्रीन पर ले जाएगा जहां आप invNorm() का उपयोग कर सकते हैं:

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में इस फ़ंक्शन का उपयोग कैसे करें।

उदाहरण 1: एकतरफ़ा परीक्षण के लिए क्रिटिकल Z मान

मान लीजिए कि एक शोधकर्ता α = 0.05 का उपयोग करके बाएं हाथ की परिकल्पना परीक्षण करता है। वह z-महत्वपूर्ण मान क्या है जो इस अल्फ़ा स्तर से मेल खाता है?

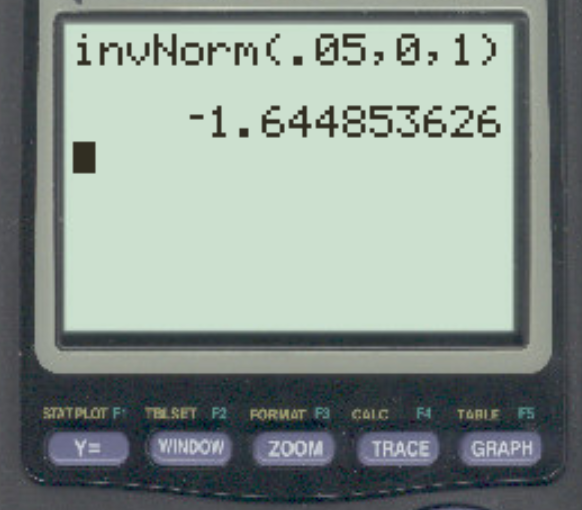
उत्तर z = -1.64485 है।

मान लीजिए कि एक शोधकर्ता α = 0.05 का उपयोग करके एक सीधी परिकल्पना परीक्षण करता है। वह z-महत्वपूर्ण मान क्या है जो इस अल्फ़ा स्तर से मेल खाता है?

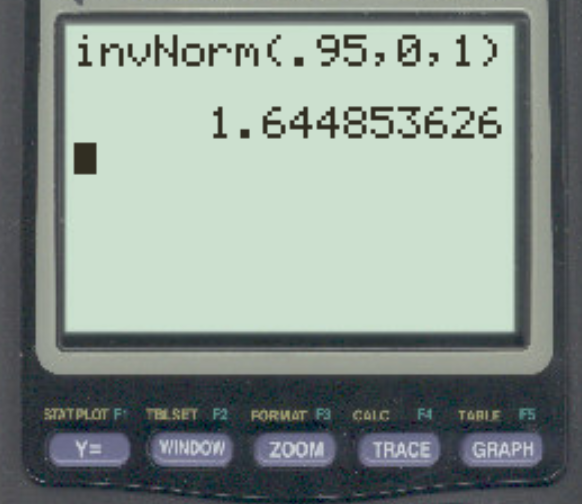
उत्तर z = 1.64485 है।

उदाहरण 2: दोतरफा परीक्षणों के लिए क्रिटिकल Z मान

मान लीजिए कि एक शोधकर्ता α = 0.05 का उपयोग करके दो-पुच्छ परिकल्पना परीक्षण आयोजित करता है। वह z-महत्वपूर्ण मान क्या है जो इस अल्फ़ा स्तर से मेल खाता है?

इस महत्वपूर्ण मान को खोजने के लिए, हम सूत्र 1 – α/2 का उपयोग कर सकते हैं। इस मामले में, हम प्रायिकता के लिए 1 – 0.05/2 = 0.975 का उपयोग करेंगे:

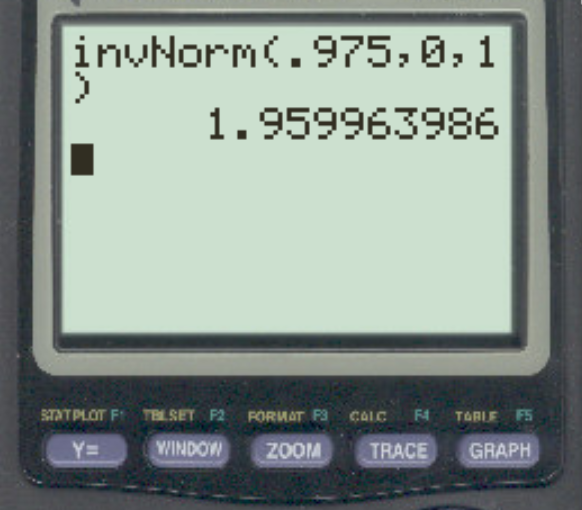
उत्तर z = 1.96 है।

उदाहरण 3: कटऑफ स्कोर के लिए महत्वपूर्ण Z मान

मान लीजिए कि किसी विशेष परीक्षा के अंक सामान्यतः 70 के माध्य और 8 के मानक विचलन के साथ वितरित किए जाते हैं। कौन सा अंक शीर्ष 10% को बाकियों से अलग करता है?

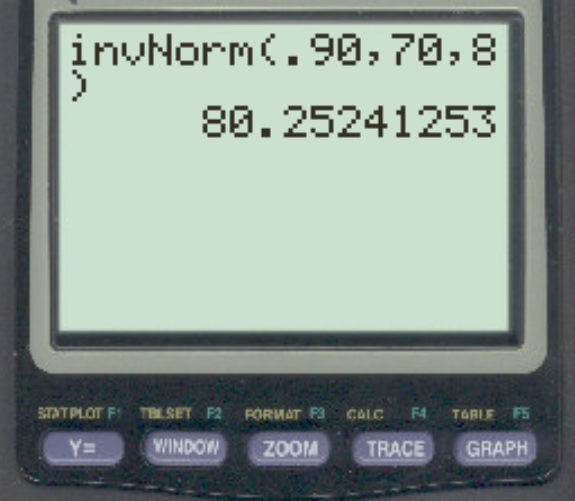
उत्तर 80.25 है।

मान लीजिए कि किसी विशेष शहर में पुरुषों की ऊंचाई सामान्यतः 68 इंच के औसत और 4 इंच के मानक विचलन के साथ वितरित की जाती है। कितनी ऊँचाई निचले 25% को बाकियों से अलग करती है?

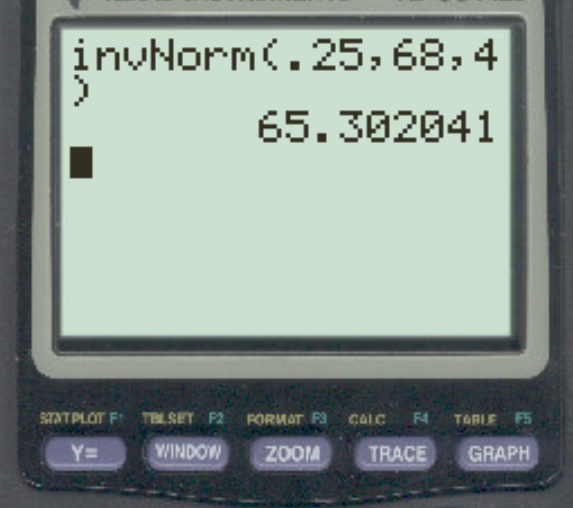
उत्तर 65.3 इंच है.

अतिरिक्त संसाधन

TI-84 कैलकुलेटर पर द्विपद संभावनाओं की गणना कैसे करें
TI-84 कैलकुलेटर पर पॉइसन संभावनाओं की गणना कैसे करें
TI-84 कैलकुलेटर पर ज्यामितीय संभावनाओं की गणना कैसे करें