एनोवा में उच्च f मान का क्या अर्थ है?
एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधन बराबर हैं या नहीं।
एक-तरफ़ा एनोवा निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:
- एच 0 : सभी समूह साधन समान हैं।
- एच ए : कम से कम एक समूह का औसत दूसरों से अलग है।
हर बार जब आप एक-तरफ़ा एनोवा निष्पादित करते हैं, तो आपके पास एक सारांश तालिका होगी जो निम्नलिखित की तरह दिखती है:
| स्रोत | वर्गों का योग (एसएस) | डीएफ | माध्य वर्ग (एमएस) | एफ | पी-मूल्य |
|---|---|---|---|---|---|
| इलाज | 192.2 | 2 | 96.1 | 2,358 | 0.1138 |
| गलती | 1100.6 | 27 | 40.8 | ||
| कुल | 1292.8 | 29 |
तालिका में F मान की गणना इस प्रकार की जाती है:
- एफ मान = माध्य वर्ग प्रसंस्करण / माध्य वर्ग त्रुटि
इसे लिखने का दूसरा तरीका यह है:
- एफ-मूल्य = नमूना साधनों के बीच भिन्नता / नमूनों के भीतर भिन्नता
यदि प्रत्येक नमूने के भीतर भिन्नता की तुलना में नमूना साधनों के बीच भिन्नता अधिक है, तो एफ मान बड़ा होगा।
उदाहरण के लिए, उपरोक्त तालिका में F मान की गणना इस प्रकार की जाती है:
- एफ-मान = 96.1 / 40.8 = 2.358
इस एफ-वैल्यू से संबंधित पी-वैल्यू को खोजने के लिए, हम अंश में स्वतंत्रता की डिग्री = डीएफ उपचार और हर में स्वतंत्रता की डिग्री = डीएफ त्रुटि के साथ एफ-वितरण कैलकुलेटर का उपयोग कर सकते हैं।
उदाहरण के लिए, पी-मान जो 2.358 के एफ-मान से मेल खाता है, अंश डीएफ = 2, और हर डीएफ = 27 0.1138 है।
चूँकि यह p-मान α = 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। इसका मतलब यह है कि तीनों समूहों के साधनों के बीच कोई सांख्यिकीय महत्वपूर्ण अंतर नहीं है।
एनोवा का एफ मान देखें
एनोवा तालिका में एफ मान की सहज समझ हासिल करने के लिए, निम्नलिखित उदाहरण पर विचार करें।
मान लीजिए कि हम यह निर्धारित करने के लिए एक-तरफ़ा एनोवा का प्रदर्शन करना चाहते हैं कि क्या तीन अलग-अलग अध्ययन तकनीकें अलग-अलग औसत परीक्षा स्कोर उत्पन्न करती हैं। निम्नलिखित तालिका प्रत्येक तकनीक का उपयोग करने वाले 10 छात्रों के परीक्षा परिणाम दिखाती है:
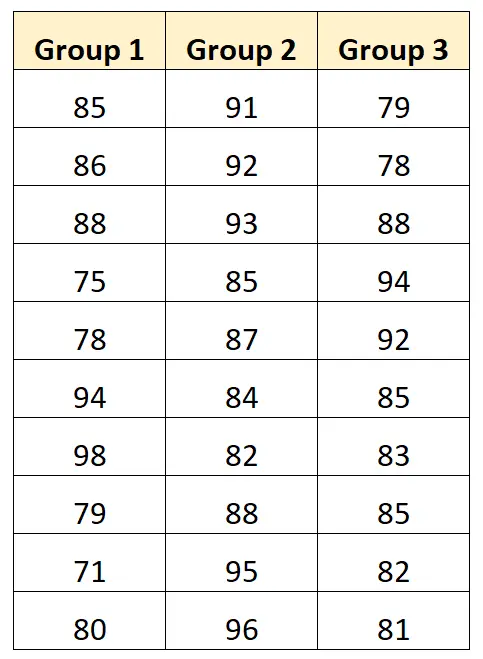
हम समूह द्वारा परीक्षा परिणाम देखने के लिए निम्नलिखित चार्ट बना सकते हैं:
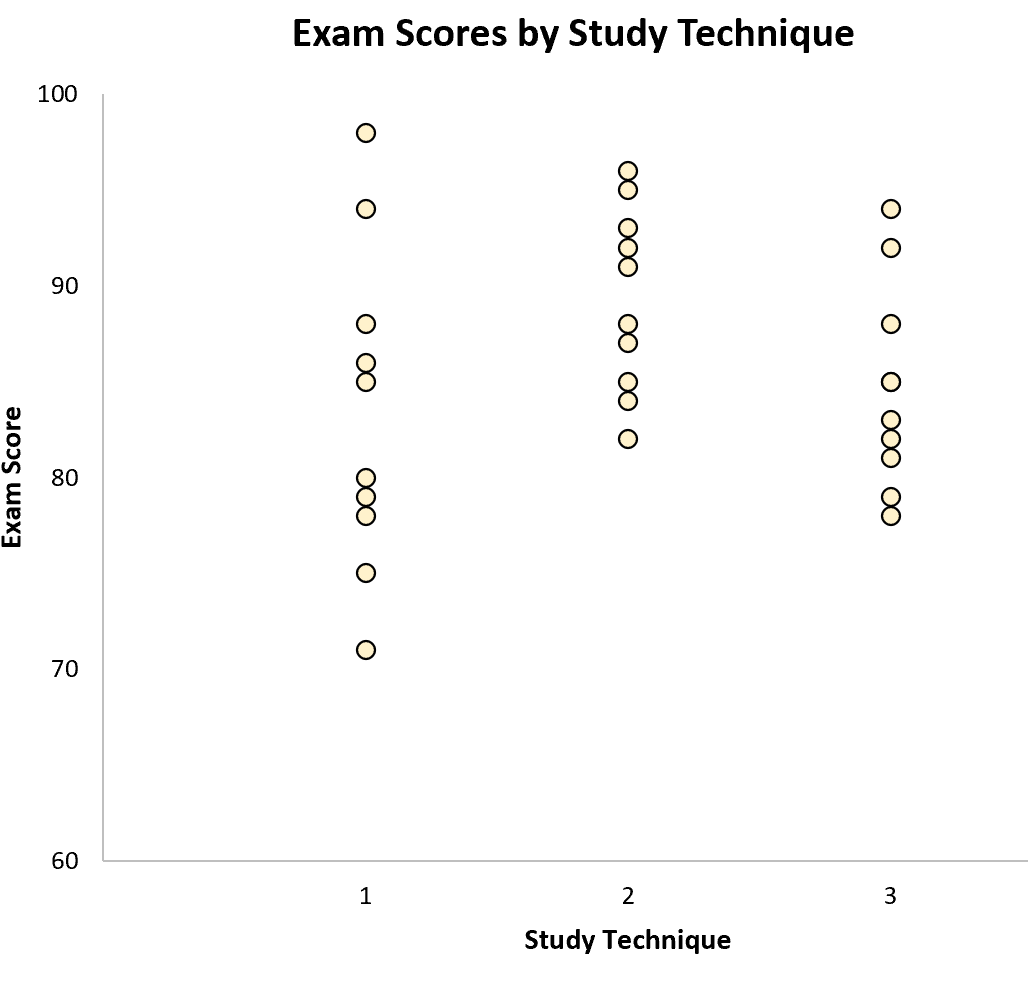
नमूनों के भीतर भिन्नता को प्रत्येक व्यक्तिगत नमूने के भीतर मूल्यों के वितरण द्वारा दर्शाया जाता है:
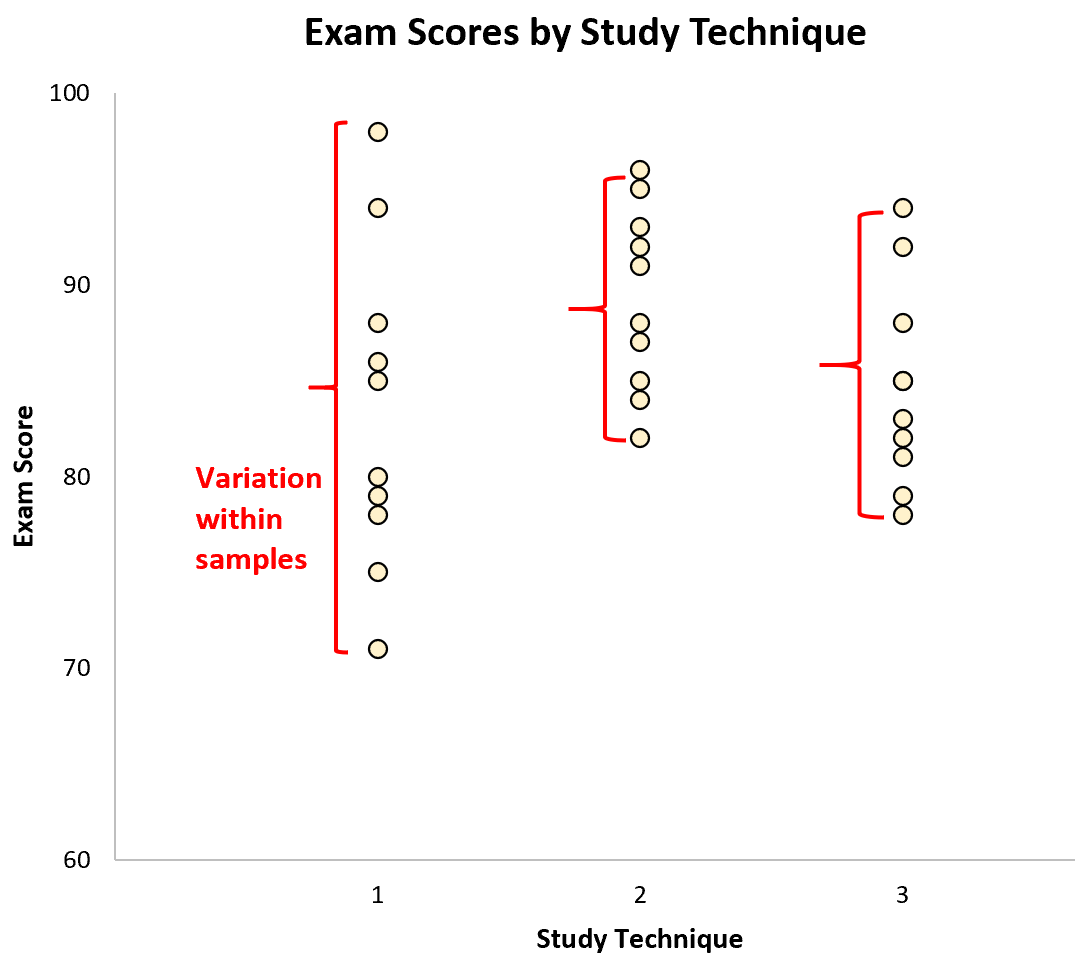
नमूनों के बीच भिन्नता को नमूना साधनों के बीच अंतर द्वारा दर्शाया जाता है:
इस डेटासेट के लिए एक-तरफ़ा एनोवा का प्रदर्शन करते हुए, हम पाते हैं कि एफ-मान 2.358 है और संबंधित पी-मान 0.1138 है।
चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि इस्तेमाल की गई अध्ययन तकनीक के परिणामस्वरूप औसत परीक्षा अंकों में सांख्यिकीय रूप से महत्वपूर्ण अंतर होता है।
दूसरे शब्दों में, यह हमें बताता है कि नमूना साधनों के बीच भिन्नता नमूनों के भीतर भिन्नता के सापेक्ष इतनी अधिक नहीं है कि शून्य परिकल्पना को अस्वीकार किया जा सके।
निष्कर्ष
यहां इस लेख के मुख्य बिंदुओं का संक्षिप्त सारांश दिया गया है:
- एनोवा में एफ मान की गणना इस प्रकार की जाती है: नमूना साधनों के बीच भिन्नता / नमूनों के भीतर भिन्नता।
- एनोवा में एफ मान जितना अधिक होगा, नमूनों के भीतर भिन्नता के सापेक्ष नमूने के बीच भिन्नता उतनी ही अधिक होगी।
- F मान जितना अधिक होगा, संगत p मान उतना ही कम होगा।
- यदि पी-मान एक निश्चित सीमा से नीचे है (जैसे α = 0.05), तो हम एनोवा की शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि समूह के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है।
अतिरिक्त संसाधन
एक्सेल में वन-वे एनोवा कैसे करें
एक-तरफ़ा एनोवा को मैन्युअल रूप से कैसे निष्पादित करें
एक तरफ़ा एनोवा कैलकुलेटर