पूर्ण बहुसंरेखता क्या है? (परिभाषा एवं उदाहरण)
आँकड़ों में, बहुसंरेखता तब होती है जब दो या दो से अधिक भविष्यवक्ता चर एक-दूसरे के साथ अत्यधिक सहसंबद्ध होते हैं, जैसे कि वे प्रतिगमन मॉडल में अद्वितीय या स्वतंत्र जानकारी प्रदान नहीं करते हैं।
यदि चर के बीच सहसंबंध की डिग्री काफी अधिक है, तो यह प्रतिगमन मॉडल को फिट करने और व्याख्या करने में समस्याएं पैदा कर सकता है।
बहुसंरेखता के सबसे चरम मामले को पूर्ण बहुसंरेखता कहा जाता है। ऐसा तब होता है जब दो या दो से अधिक भविष्यवक्ता चर का एक दूसरे के साथ सटीक रैखिक संबंध होता है।
उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित डेटा सेट है:
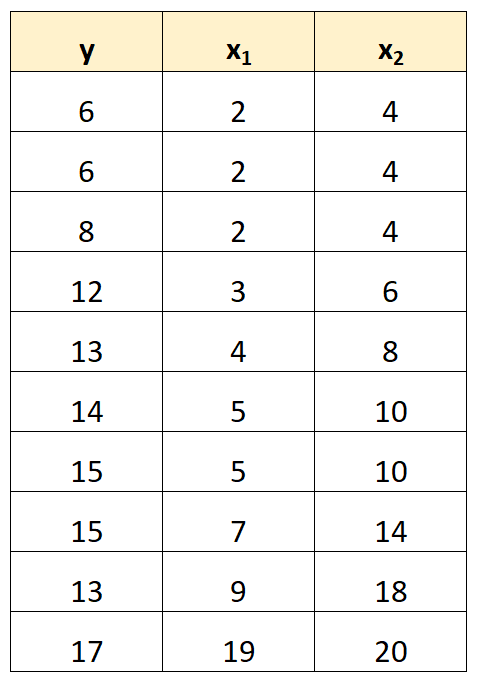
ध्यान दें कि भविष्यवक्ता चर x 2 के मान केवल 2 से गुणा किए गए x 1 के मान हैं।
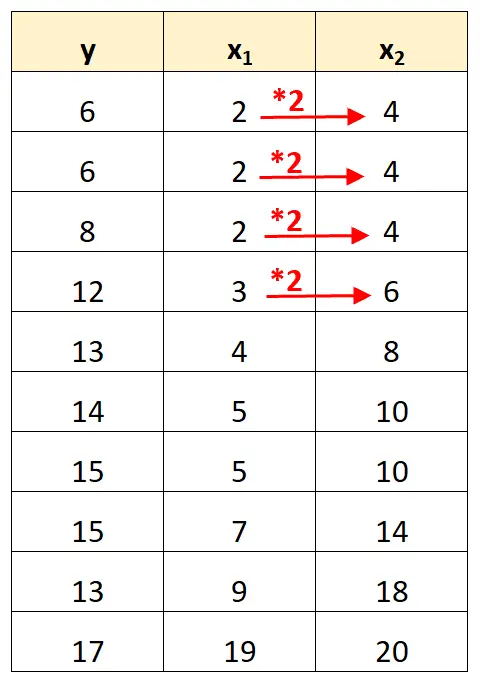
यह पूर्ण बहुसंरेखता का एक उदाहरण है।
पूर्ण बहुसंरेखता की समस्या
जब किसी डेटा सेट में पूर्ण बहुसंरेखता मौजूद होती है, तो साधारण न्यूनतम वर्ग प्रतिगमन गुणांक का अनुमान लगाने में असमर्थ होता है।
वास्तव में, किसी अन्य भविष्यवक्ता चर (x 2 ) को स्थिर रखते हुए प्रतिक्रिया चर (y) पर एक भविष्यवक्ता चर (x 1 ) के सीमांत प्रभाव का अनुमान लगाना संभव नहीं है क्योंकि x 2 हमेशा ठीक उसी तरह चलता है जब x 1 चलता है।
संक्षेप में, पूर्ण बहुसंरेखता एक प्रतिगमन मॉडल में प्रत्येक गुणांक के लिए एक मूल्य का अनुमान लगाना असंभव बना देती है।
पूर्ण बहुसंरेखता से कैसे निपटें
पूर्ण बहुसंरेखता को संभालने का सबसे सरल तरीका उन चरों में से एक को हटाना है जिनका दूसरे चर के साथ सटीक रैखिक संबंध है।
उदाहरण के लिए, हमारे पिछले डेटासेट में, हम केवल पूर्वसूचक चर के रूप में x 2 को हटा सकते हैं।
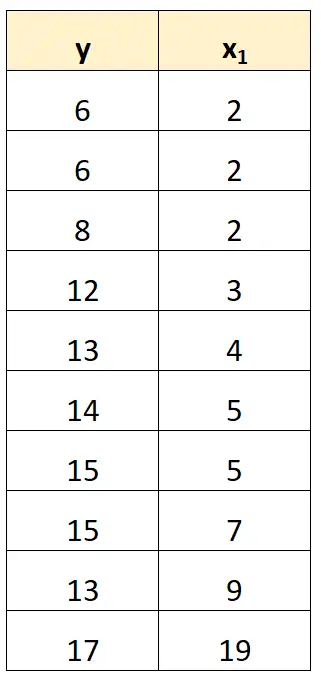
फिर हम पूर्वसूचक चर के रूप में x 1 और प्रतिक्रिया चर के रूप में y का उपयोग करके एक प्रतिगमन मॉडल फिट करेंगे।
पूर्ण बहुसंरेखता के उदाहरण
निम्नलिखित उदाहरण व्यवहार में पूर्ण बहुसंरेखता के तीन सबसे सामान्य परिदृश्य दिखाते हैं।
1. एक भविष्यवक्ता चर दूसरे का गुणज है
मान लीजिए कि हम डॉल्फ़िन की एक निश्चित प्रजाति के वजन का अनुमान लगाने के लिए “सेंटीमीटर में ऊंचाई” और “मीटर में ऊंचाई” का उपयोग करना चाहते हैं।
हमारा डेटासेट इस तरह दिख सकता है:
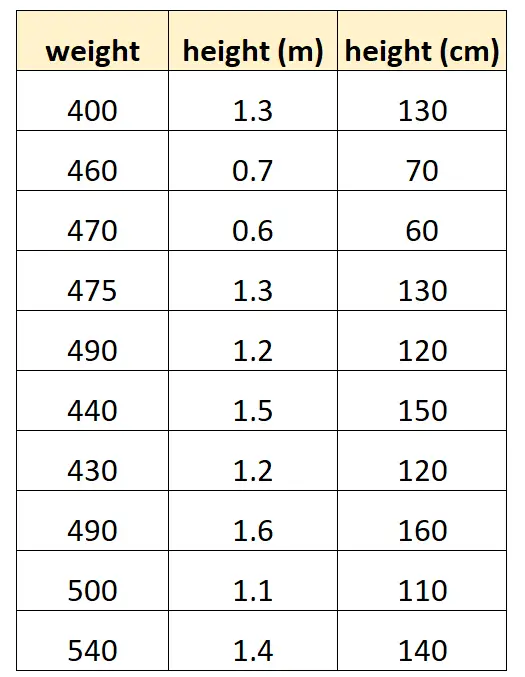
ध्यान दें कि “सेंटीमीटर में ऊंचाई” का मान “मीटर में ऊंचाई” को 100 से गुणा करने के बराबर है। यह पूर्ण बहुसंरेखता का मामला है।
यदि हम इस डेटासेट का उपयोग करके आर में एक एकाधिक रैखिक प्रतिगमन मॉडल को फिट करने का प्रयास करते हैं, तो हम भविष्यवक्ता चर “मीटर” के लिए गुणांक अनुमान का उत्पादन करने में सक्षम नहीं होंगे:
#define data df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540), m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4), cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140)) #fit multiple linear regression model model <- lm(weight~m+cm, data=df) #view summary of model summary(model) Call: lm(formula = weight ~ m + cm, data = df) Residuals: Min 1Q Median 3Q Max -70,501 -25,501 5,183 19,499 68,590 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 458,676 53,403 8,589 2.61e-05 *** m 9.096 43.473 0.209 0.839 cm NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 41.9 on 8 degrees of freedom Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395
2. एक भविष्यवक्ता चर दूसरे का रूपांतरित संस्करण है
मान लीजिए कि हम बास्केटबॉल खिलाड़ियों की रेटिंग की भविष्यवाणी करने के लिए “अंक” और “स्केल किए गए अंक” का उपयोग करना चाहते हैं।
मान लीजिए कि चर “स्केल्ड पॉइंट” की गणना इस प्रकार की जाती है:
स्केल किए गए अंक = (अंक – μ अंक ) / σ अंक
हमारा डेटासेट इस तरह दिख सकता है:
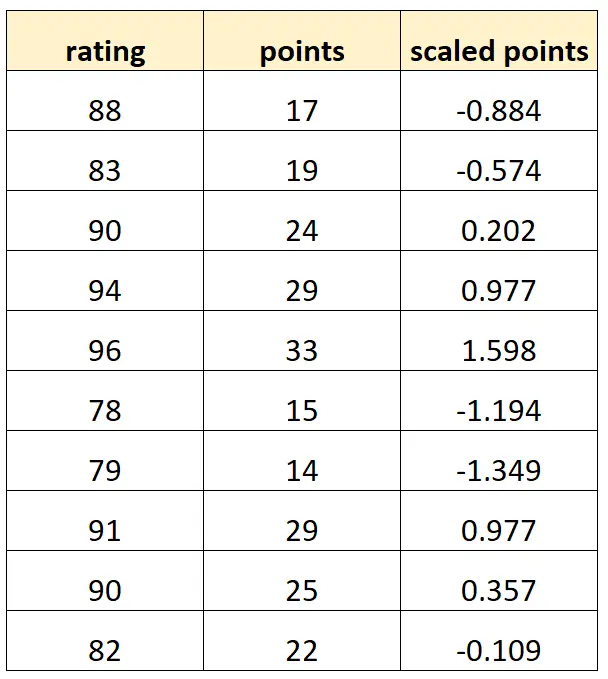
ध्यान दें कि प्रत्येक “स्केल्ड पॉइंट” मान केवल “पॉइंट्स” का एक मानकीकृत संस्करण है। यह पूर्ण बहुसंरेखता का मामला है।
यदि हम इस डेटासेट का उपयोग करके आर में एक एकाधिक रैखिक प्रतिगमन मॉडल को फिट करने का प्रयास करते हैं, तो हम “स्केल किए गए बिंदु” भविष्यवक्ता चर के लिए गुणांक अनुमान का उत्पादन करने में सक्षम नहीं होंगे:
#define data df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82), pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22)) df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts) #fit multiple linear regression model model <- lm(rating~pts+scaled_pts, data=df) #view summary of model summary(model) Call: lm(formula = rating ~ pts + scaled_pts, data = df) Residuals: Min 1Q Median 3Q Max -4.4932 -1.3941 -0.2935 1.3055 5.8412 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 67.4218 3.5896 18.783 6.67e-08 *** pts 0.8669 0.1527 5.678 0.000466 *** scaled_pts NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.953 on 8 degrees of freedom Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663
3. डमी वैरिएबल ट्रैप
एक अन्य परिदृश्य जिसमें पूर्ण बहुसंरेखता घटित हो सकती है उसे डमी वेरिएबल ट्रैप के रूप में जाना जाता है। यह तब होता है जब हम एक प्रतिगमन मॉडल में एक श्रेणीबद्ध चर लेना चाहते हैं और इसे “डमी वैरिएबल” में परिवर्तित करना चाहते हैं जो 0, 1, 2, आदि के मान लेता है।
उदाहरण के लिए, मान लें कि हम आय की भविष्यवाणी करने के लिए भविष्यवक्ता चर “आयु” और “वैवाहिक स्थिति” का उपयोग करना चाहते हैं:

भविष्यवक्ता चर के रूप में “वैवाहिक स्थिति” का उपयोग करने के लिए, हमें पहले इसे एक डमी चर में परिवर्तित करना होगा।
ऐसा करने के लिए, हम “एकल” को आधार मान के रूप में छोड़ सकते हैं, क्योंकि ऐसा अक्सर होता है, और “विवाहित” और “तलाक” को 0 या 1 का मान निम्नानुसार निर्दिष्ट कर सकते हैं:

निम्नानुसार तीन नए डमी वेरिएबल बनाना एक गलती होगी:

इस मामले में, “एकल” चर “विवाहित” और “तलाकशुदा” चर का एक आदर्श रैखिक संयोजन है। यह पूर्ण बहुसंरेखता का एक उदाहरण है।
यदि हम इस डेटासेट का उपयोग करके आर में एक एकाधिक रैखिक प्रतिगमन मॉडल को फिट करने का प्रयास करते हैं, तो हम प्रत्येक भविष्यवक्ता चर के लिए गुणांक अनुमान का उत्पादन करने में सक्षम नहीं होंगे:
#define data df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107), age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53), single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0), married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1), divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0)) #fit multiple linear regression model model <- lm(income~age+single+married+divorced, data=df) #view summary of model summary(model) Call: lm(formula = income ~ age + single + married + divorced, data = df) Residuals: Min 1Q Median 3Q Max -9.7075 -5.0338 0.0453 3.3904 12.2454 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 16.7559 17.7811 0.942 0.37739 age 1.4717 0.3544 4.152 0.00428 ** single -2.4797 9.4313 -0.263 0.80018 married NA NA NA NA divorced -8.3974 12.7714 -0.658 0.53187 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 8.391 on 7 degrees of freedom Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865
अतिरिक्त संसाधन
प्रतिगमन में बहुसंरेखता और वीआईएफ के लिए एक गाइड
आर में वीआईएफ की गणना कैसे करें
पायथन में वीआईएफ की गणना कैसे करें
एक्सेल में वीआईएफ की गणना कैसे करें