नकारात्मक द्विपद वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि नकारात्मक द्विपद वितरण क्या है और इसका उपयोग किस लिए किया जाता है। आपको ऋणात्मक द्विपद बंटन का सूत्र, एक ठोस उदाहरण और इस प्रकार के संभाव्यता बंटन के गुण भी मिलेंगे। अंत में, आप ऑनलाइन कैलकुलेटर से किसी भी नकारात्मक द्विपद वितरण संभावना की गणना करने में सक्षम होंगे।

ऋणात्मक द्विपद बंटन क्या है?

नकारात्मक द्विपद वितरण एक संभाव्यता वितरण है जो एक निश्चित संख्या में सकारात्मक परिणाम प्राप्त करने के लिए आवश्यक बर्नौली परीक्षणों की संख्या का वर्णन करता है।

इसलिए, एक नकारात्मक द्विपद वितरण में दो विशिष्ट पैरामीटर होते हैं: आर वांछित सफल परिणामों की संख्या है और पी प्रत्येक बर्नौली प्रयोग के लिए सफलता की संभावना है।

$X\sim \text{BN}(r,p)$

याद रखें कि बर्नौली परीक्षण एक ऐसा प्रयोग है जिसके दो संभावित परिणाम हैं: “सफलता” और “असफलता।” इसलिए यदि “सफलता” की संभावना p है, तो “असफलता” की संभावना q=1-p है।

इस प्रकार, एक नकारात्मक द्विपद वितरण एक ऐसी प्रक्रिया को परिभाषित करता है जिसमें सकारात्मक परिणाम प्राप्त करने के लिए आवश्यकतानुसार कई बर्नौली परीक्षण किए जाते हैं। इसके अलावा, ये सभी बर्नौली परीक्षण स्वतंत्र हैं और इनमें सफलता की निरंतर संभावना है।

उदाहरण के लिए, एक यादृच्छिक चर जो एक नकारात्मक द्विपद वितरण का अनुसरण करता है वह संख्या है कि एक पासे को कितनी बार घुमाया जाना चाहिए जब तक कि संख्या 6 को तीन बार न घुमाया जाए।

एक नकारात्मक द्विपद वितरण और एक द्विपद वितरण के बीच अंतर यह है कि नकारात्मक द्विपद वितरण एक निश्चित संख्या में सफल परिणाम प्राप्त करने में लगने वाले समय की संख्या की गणना करता है, जबकि द्विपद वितरण एक श्रृंखला बर्नौली परीक्षणों में सफल मामलों की संख्या की गणना करता है।

➤ देखें: द्विपद बंटन क्या है?

नकारात्मक द्विपद वितरण सूत्र

पैरामीटर r, p, x को देखते हुए, नकारात्मक द्विपद वितरण की संभावना की गणना xr में x-1 की संयोजन संख्या को (1-p) ^xr को p ^r से गुणा करके की जाती है।

तो, एक नकारात्मक द्विपद वितरण संभावना की गणना करने का सूत्र है:

👉 आप नकारात्मक द्विपद वितरण का अनुसरण करने वाले एक चर की संभावना की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

ऋणात्मक द्विपद बंटन का हल किया गया अभ्यास

इसकी क्या प्रायिकता है कि यदि आप एक सिक्के को आठ बार उछालते हैं, तो आठवीं बार उछालने पर वह चौथी बार शीर्ष पर आ जाएगा?

सबसे पहले, हमें सिक्के को उछालने पर चित आने की प्रायिकता की गणना करनी होगी। इस मामले में, हमारे पास दो संभावित परिणामों (हेड और टेल) में से केवल एक सकारात्मक परिणाम (हेड) है, इसलिए सफलता की संभावना है:

$p=\cfrac{1}{2}=0,5$

इस प्रकार, इस समस्या में यादृच्छिक चर एक नकारात्मक द्विपद वितरण का अनुसरण करता है जहां r=4 और p=0.5। इसलिए, हम उस संभावना की गणना करने के लिए नकारात्मक द्विपद वितरण सूत्र का उपयोग करते हैं जो अभ्यास हमें करने के लिए कहता है।

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

ऋणात्मक द्विपद वितरण के लक्षण

नकारात्मक द्विपद वितरण की सबसे महत्वपूर्ण विशेषताएँ नीचे दी गई हैं।

नकारात्मक द्विपद वितरण को दो विशिष्ट मापदंडों द्वारा परिभाषित किया गया है: आर वांछित सफल परिणामों की संख्या है और पी प्रत्येक बर्नौली प्रयोग के लिए सफलता की संभावना है।

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

ऋणात्मक द्विपद वितरण का प्रसरण r को (1-p) से गुणा करके p ² से विभाजित करने के बराबर होता है।

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

यदि पैरामीटर r 1 से अधिक है, तो नकारात्मक द्विपद वितरण के मोड की गणना निम्न सूत्र से की जा सकती है:

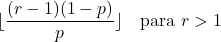
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li> द्रव्यमान फ़ंक्शन जो नकारात्मक द्विपद वितरण की संभावना निर्धारित करना संभव बनाता है वह इस प्रकार है:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

एक नकारात्मक द्विपद वितरण के विषमता गुणांक की गणना निम्नलिखित अभिव्यक्ति के साथ की जाती है:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

नकारात्मक द्विपद वितरण का कुर्टोसिस निम्नलिखित सूत्र से पाया जा सकता है:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

यदि पैरामीटर r 1 के बराबर है, तो हमारे पास ज्यामितीय वितरण का मामला है।

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

नकारात्मक द्विपद वितरण कैलकुलेटर

संभाव्यता की गणना करने के लिए निम्नलिखित कैलकुलेटर में पैरामीटर आर, पी, एक्स के मान दर्ज करें। आपको दशमलव विभाजक के रूप में बिंदु का उपयोग करके संख्याएँ दर्ज करनी होंगी, उदाहरण के लिए 0.50।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने