एसपीएसएस में वन-वे एनोवा कैसे निष्पादित करें

एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं।

इस प्रकार के परीक्षण को वन-वे एनोवा कहा जाता है क्योंकि हम एक प्रतिक्रिया चर पर एक भविष्यवक्ता चर के प्रभाव का विश्लेषण करते हैं।

यदि हम इसके बजाय एक प्रतिक्रिया चर पर दो भविष्यवक्ता चर के प्रभाव में रुचि रखते थे, तो हम दो-तरफ़ा एनोवा प्रदर्शन कर सकते थे।

यह ट्यूटोरियल बताता है कि एसपीएसएस में एक-तरफ़ा एनोवा कैसे निष्पादित किया जाए।

उदाहरण: एसपीएसएस में वन-वे एनोवा

मान लीजिए कि एक शोधकर्ता एक अध्ययन में भाग लेने के लिए 30 छात्रों की भर्ती करता है। छात्रों को परीक्षा की तैयारी के लिए अगले महीने तीन अध्ययन तकनीकों में से एक का उपयोग करने के लिए यादृच्छिक रूप से नियुक्त किया जाता है। महीने के अंत में, सभी छात्र एक ही परीक्षा देते हैं।

छात्र परीक्षा परिणाम नीचे दिखाए गए हैं:

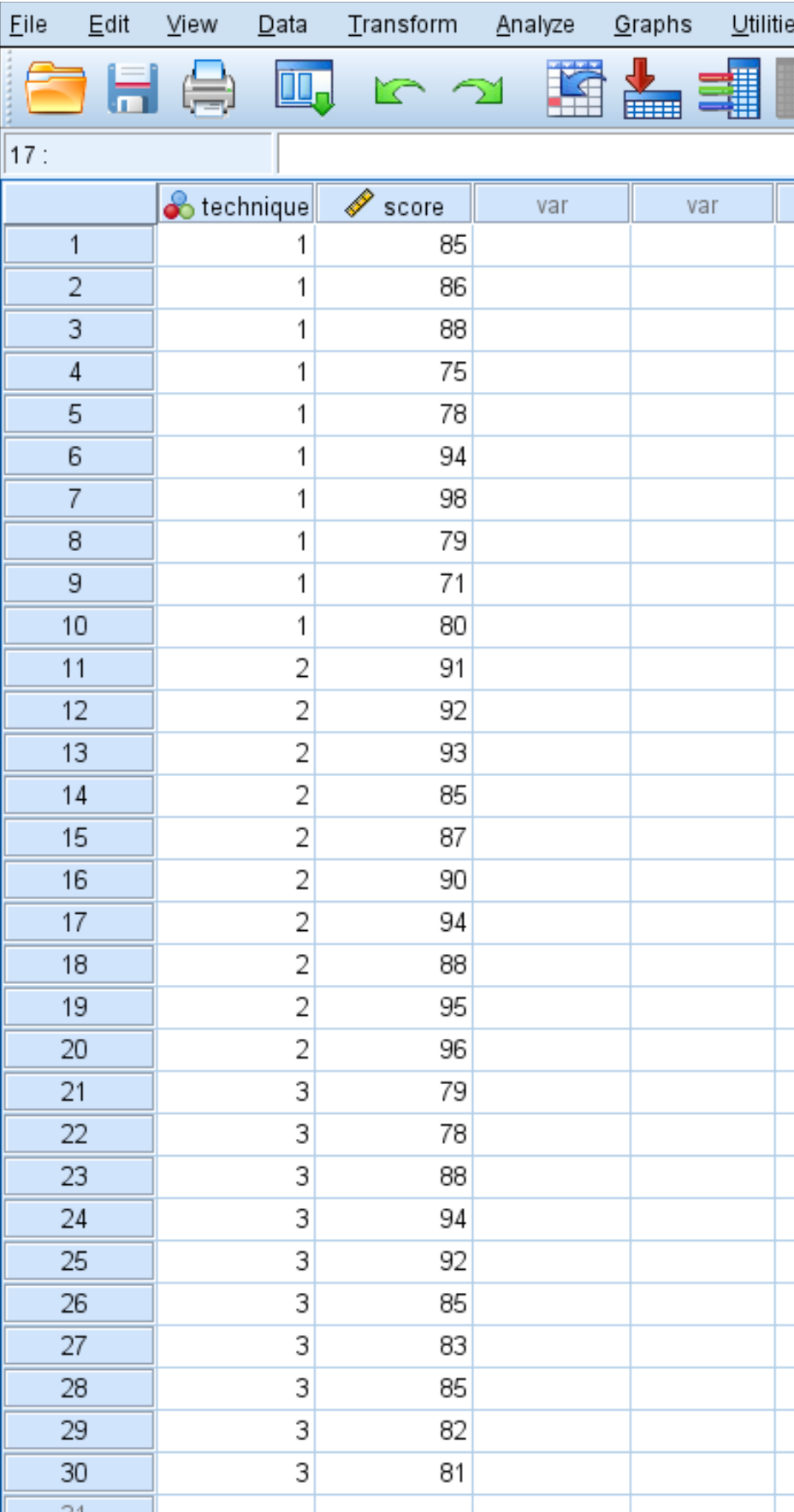
यह निर्धारित करने के लिए कि क्या तीनों समूहों में औसत स्कोर समान हैं, एक-तरफ़ा एनोवा निष्पादित करने के लिए निम्नलिखित चरणों का उपयोग करें।

चरण 1: डेटा को विज़ुअलाइज़ करें।

सबसे पहले, हम तीन अध्ययन तकनीकों में से प्रत्येक के लिए परीक्षण स्कोर के वितरण की कल्पना करने के लिए बॉक्सप्लॉट बनाएंगे। चार्ट टैब पर क्लिक करें, फिर चार्ट बिल्डर पर क्लिक करें।

इसमें से चुनें: विंडो में बॉक्सप्लॉट चुनें। फिर सिंपल बॉक्सप्लॉट लेबल वाले पहले चार्ट को मुख्य संपादन विंडो में खींचें। तकनीकी चर को x-अक्ष पर और स्कोर को y-अक्ष पर खींचें।

फिर एलिमेंट प्रॉपर्टीज पर क्लिक करें, फिर Y1 एक्सिस पर क्लिक करें । न्यूनतम मान को 60 में बदलें। फिर ठीक पर क्लिक करें।

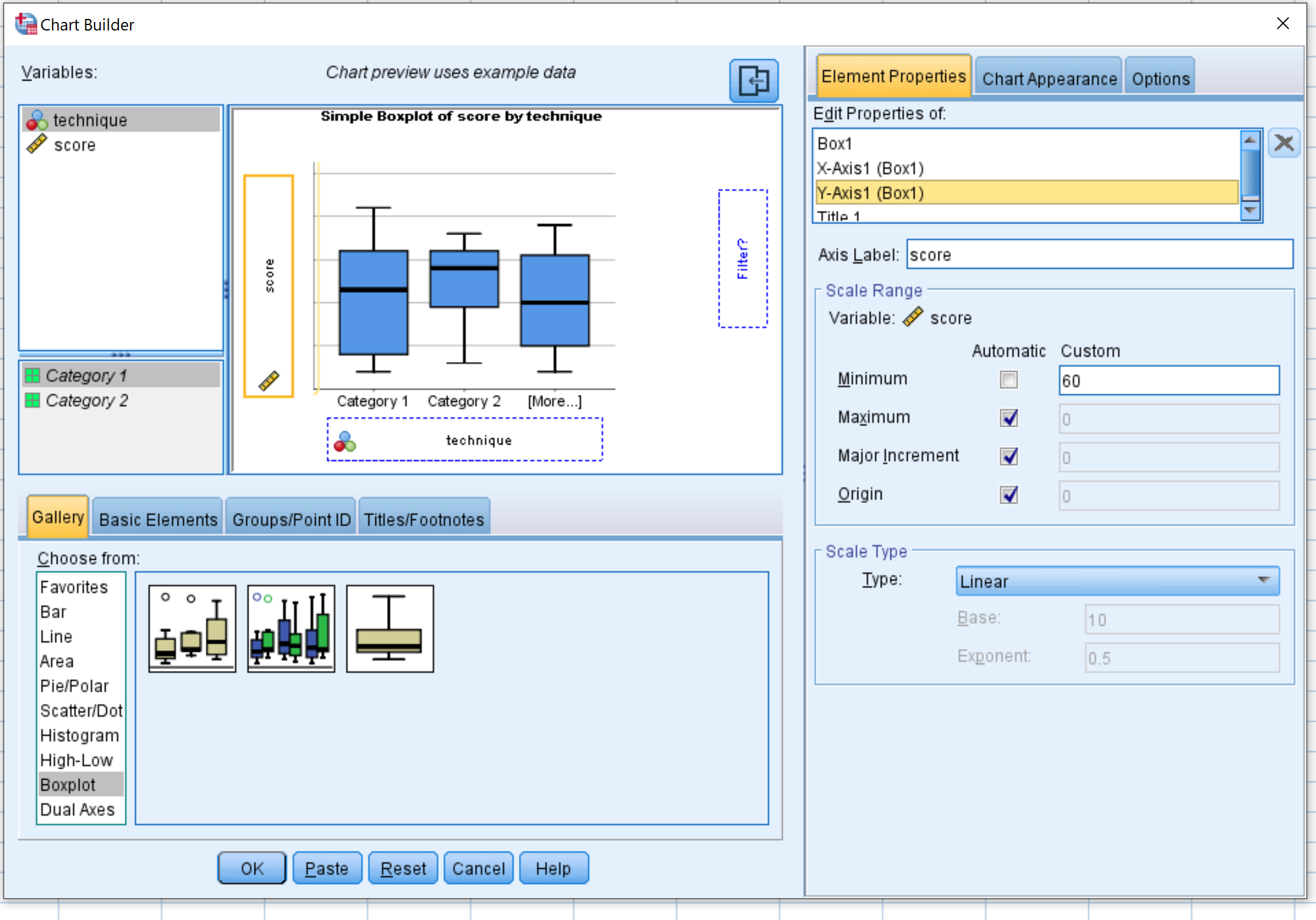
निम्नलिखित बॉक्सप्लॉट दिखाई देंगे:

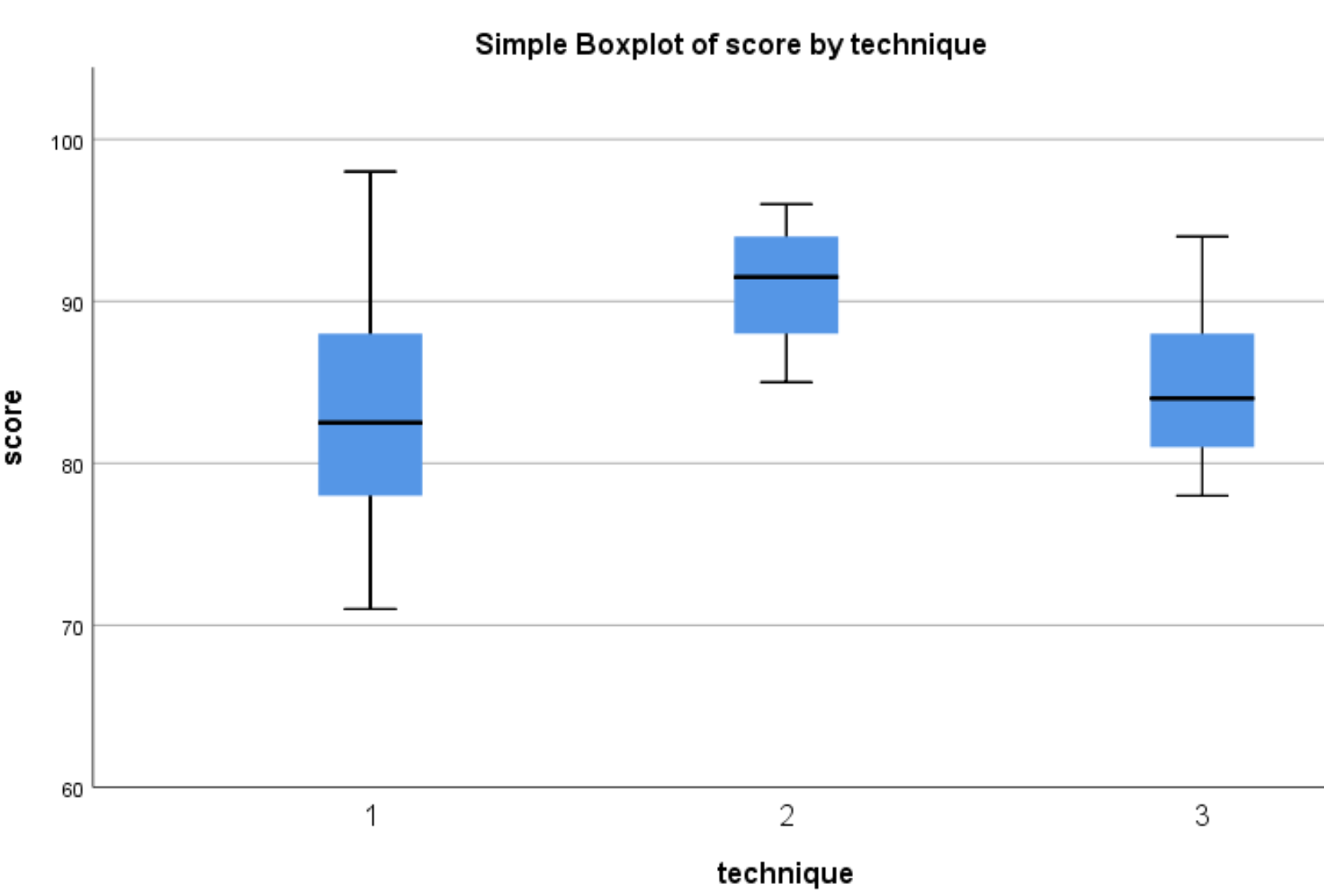
हम देख सकते हैं कि तकनीक 1 और 3 का उपयोग करने वाले छात्रों की तुलना में तकनीक 2 का उपयोग करने वाले छात्रों के लिए परीक्षण अंकों का वितरण अधिक होता है। यह निर्धारित करने के लिए कि क्या ये स्कोर अंतर सांख्यिकीय रूप से महत्वपूर्ण हैं, हम एक-तरफ़ा एनोवा का प्रदर्शन करेंगे।

चरण 2: एक-तरफ़ा एनोवा निष्पादित करें।

विश्लेषण टैब पर क्लिक करें, फिर साधनों की तुलना करें , फिर वन-वे एनोवा पर क्लिक करें ।

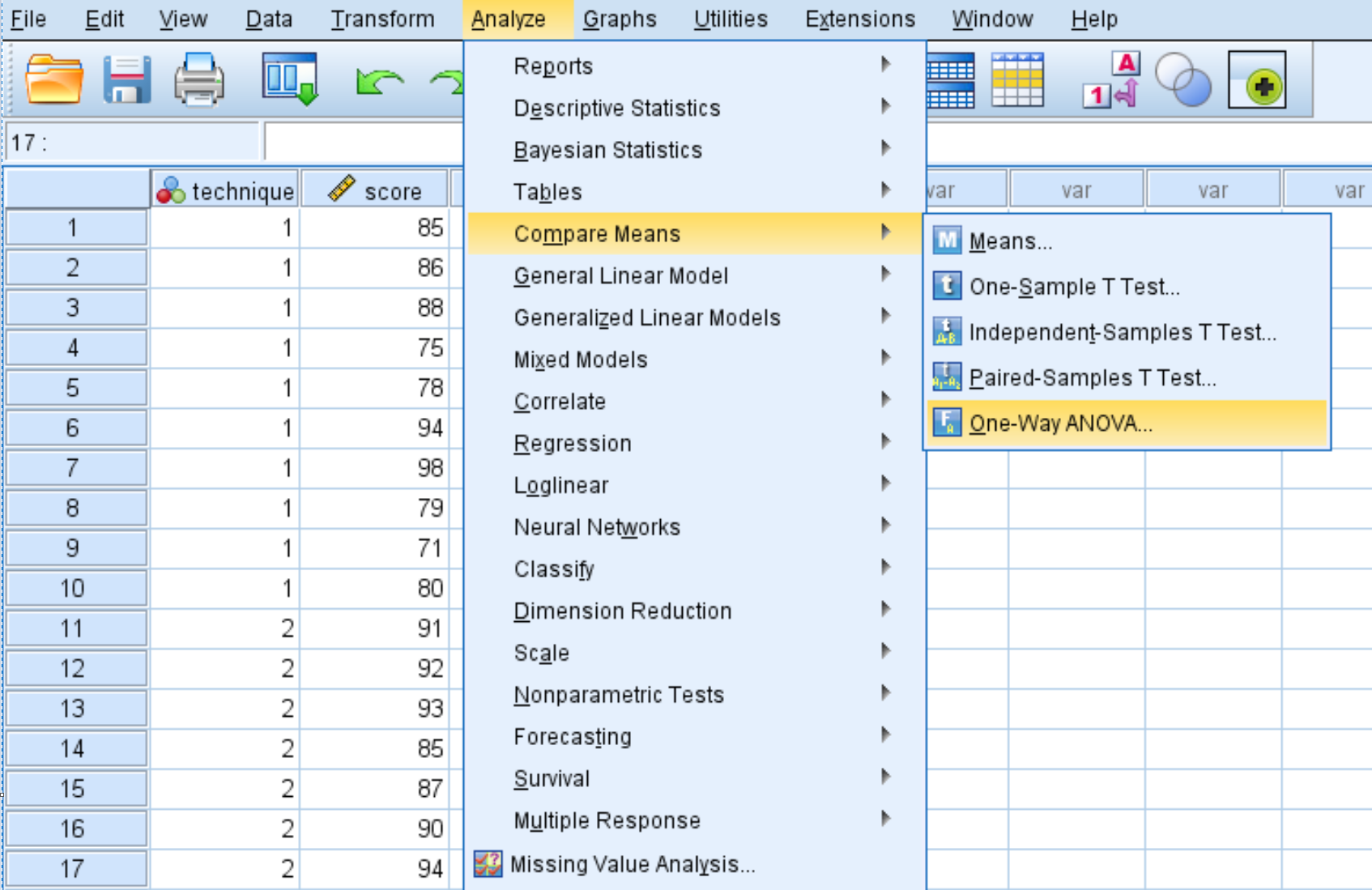
दिखाई देने वाली नई विंडो में, वेरिएबल स्कोर को डिपेंडेंट लिस्ट लेबल वाले बॉक्स में और वेरिएबल तकनीक को फैक्टर लेबल वाले बॉक्स में रखें।

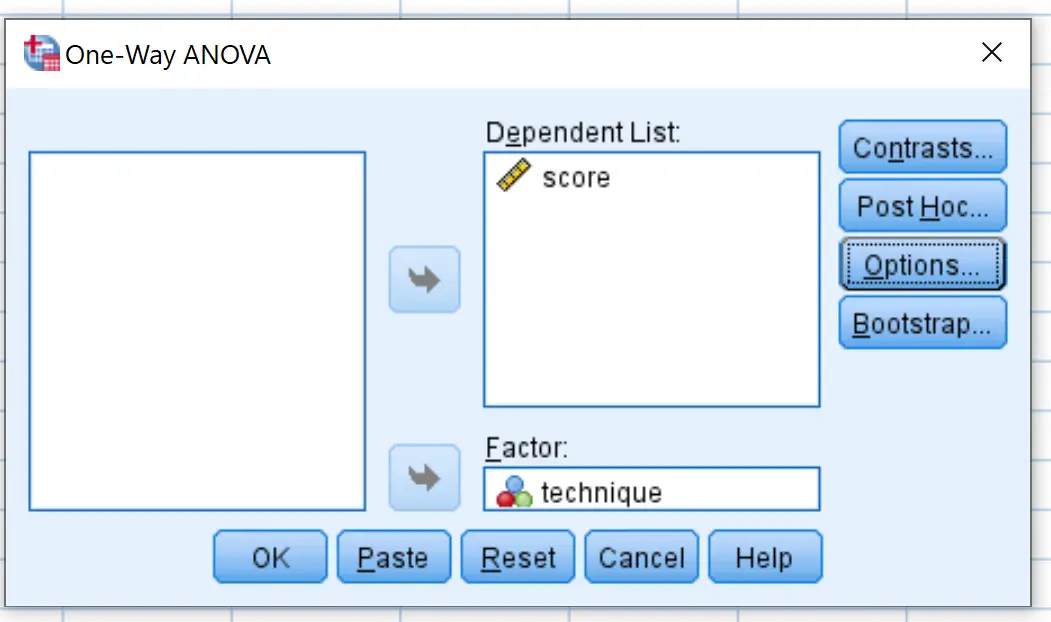
फिर पोस्ट हॉक पर क्लिक करें और टुकी के बगल में स्थित बॉक्स को चेक करें। फिर जारी रखें पर क्लिक करें.

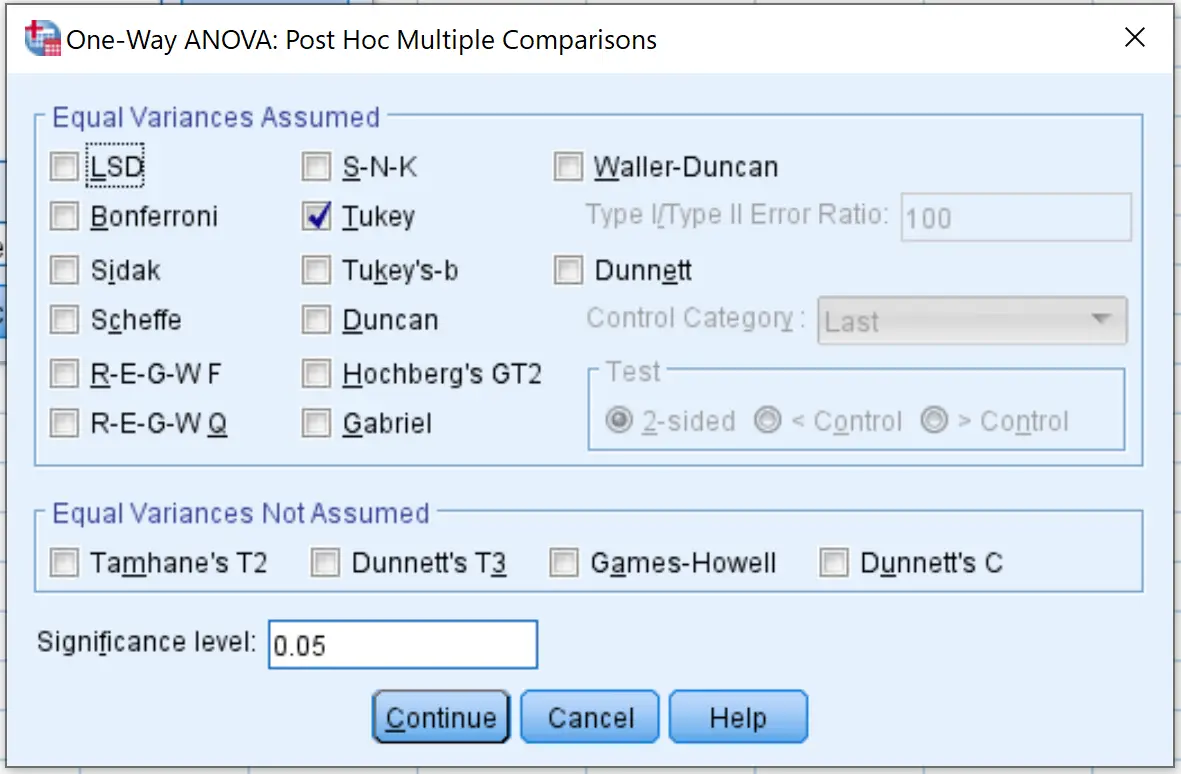
फिर विकल्प पर क्लिक करें और वर्णनात्मक के बगल में स्थित बॉक्स को चेक करें। फिर जारी रखें पर क्लिक करें.

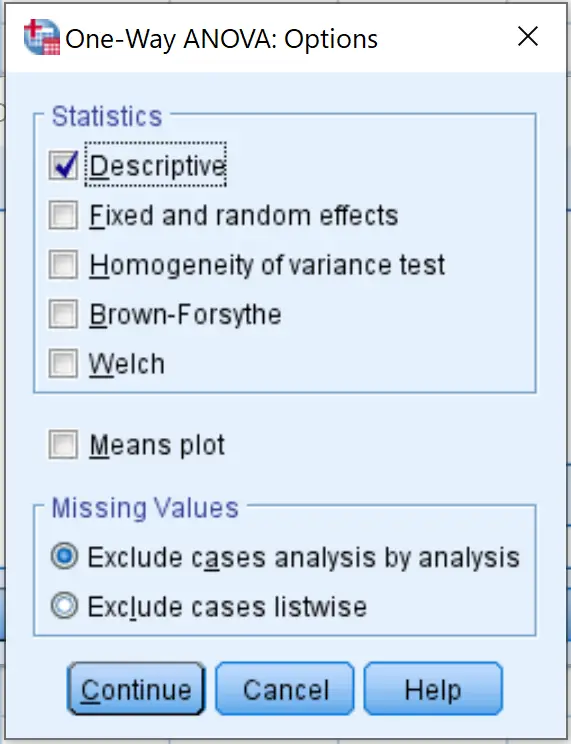
अंत में, OK पर क्लिक करें।

चरण 3: परिणाम की व्याख्या करें।

एक बार जब आप ओके पर क्लिक करते हैं, तो एकतरफा एनोवा परिणाम दिखाई देंगे। यहां परिणाम की व्याख्या करने का तरीका बताया गया है:

तालिका विवरण

यह तालिका हमारे डेटासेट में प्रत्येक तीन समूहों के लिए वर्णनात्मक आँकड़े प्रदर्शित करती है।

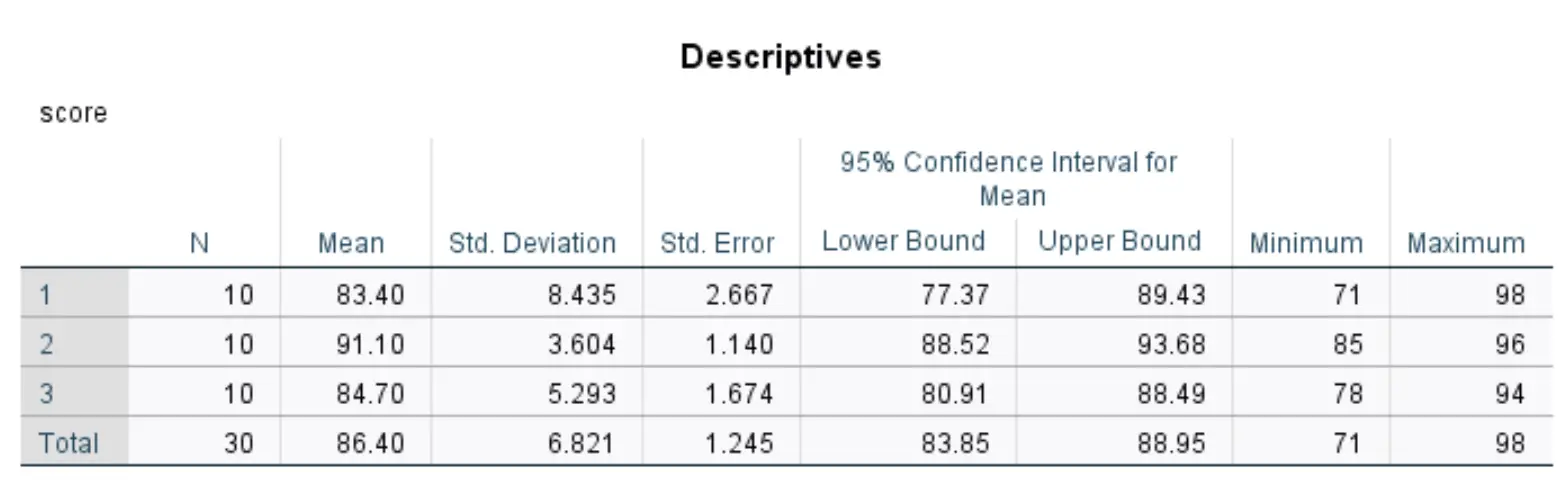
सर्वाधिक प्रासंगिक आंकड़ों में शामिल हैं:

• एन: प्रत्येक समूह में छात्रों की संख्या।
• औसत: प्रत्येक समूह के लिए औसत परीक्षण स्कोर।
• मानक। विचलन: प्रत्येक समूह के लिए परीक्षण परिणामों का मानक विचलन।

एनोवा टेबल

यह तालिका एक-तरफ़ा एनोवा के परिणाम प्रदर्शित करती है:

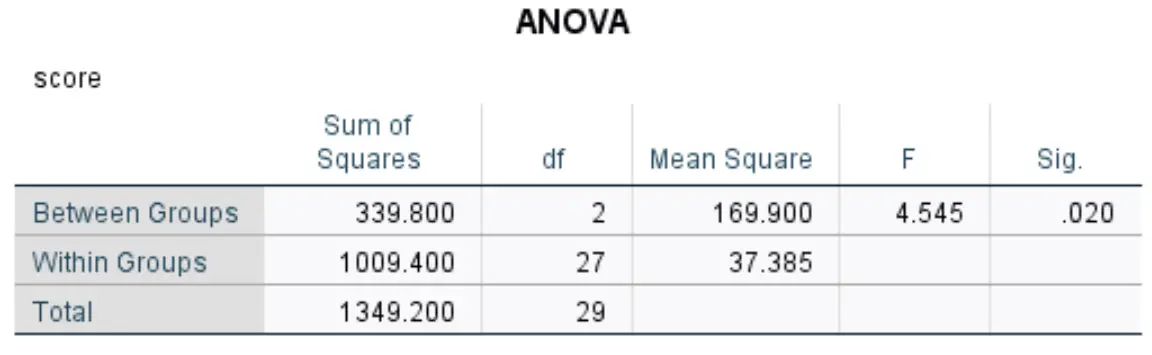
सर्वाधिक प्रासंगिक आंकड़ों में शामिल हैं:

• एफ: समग्र एफ आँकड़ा।
• हस्ताक्षर: पी-मान जो अंश डीएफ (2) और हर डीएफ (27) के साथ एफ आंकड़े (4.545) से मेल खाता है। इस स्थिति में, पी-वैल्यू 0.020 हो जाता है।

याद रखें कि एक-तरफ़ा एनोवा निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

• एच ₀ (शून्य परिकल्पना): μ ₁ = μ ₂ = μ ₃ = … = μ _k (सभी जनसंख्या साधन समान हैं)
• एच _ए (वैकल्पिक परिकल्पना): कम से कम एक जनसंख्या माध्य भिन्न है   आराम

चूँकि एनोवा तालिका का पी-मान 0.05 से कम है, हमारे पास शून्य परिकल्पना को अस्वीकार करने और यह निष्कर्ष निकालने के लिए पर्याप्त सबूत हैं कि समूह का कम से कम एक साधन दूसरों से अलग है।

यह जानने के लिए कि किस समूह का मतलब एक दूसरे से भिन्न है, हम एनोवा परिणाम की अंतिम तालिका का संदर्भ ले सकते हैं।

एकाधिक तुलना तालिका

यह तालिका तीनों समूहों में से प्रत्येक के बीच तुकी की पोस्ट-हॉक एकाधिक तुलनाएँ प्रदर्शित करती है। हम मुख्य रूप से सिग में रुचि रखते हैं। कॉलम, जो प्रत्येक समूह के बीच के अंतर के लिए पी-मान प्रदर्शित करता है:

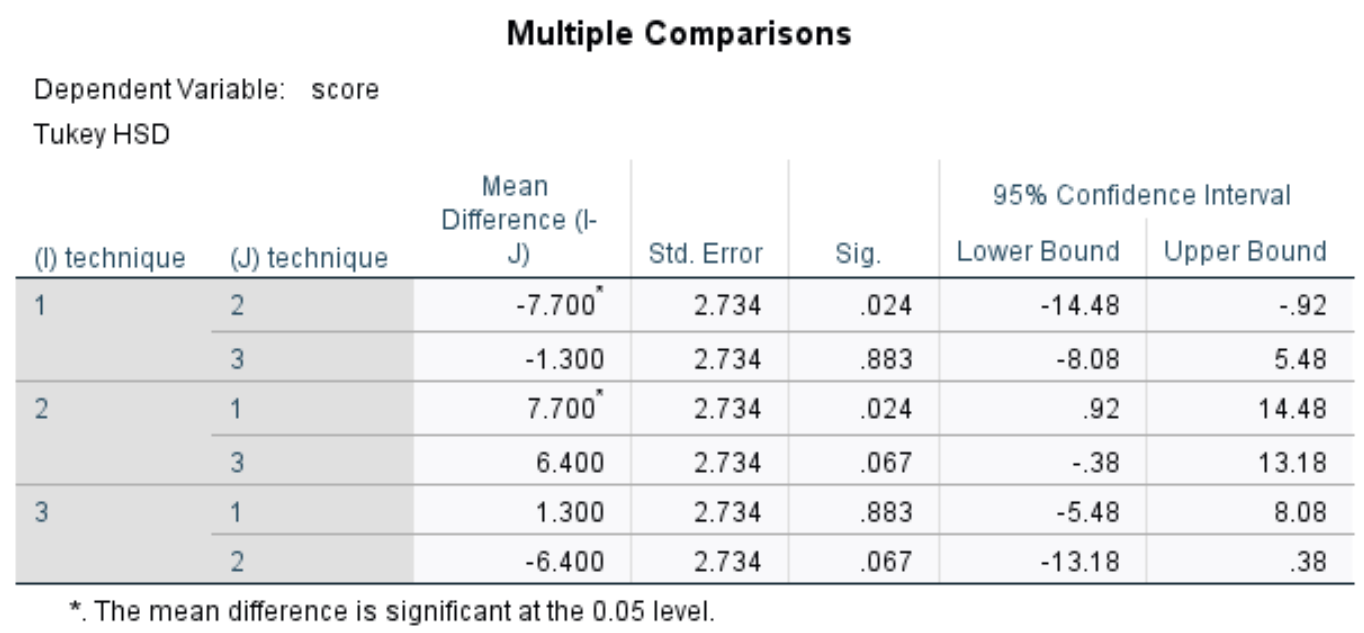
तालिका में हम निम्नलिखित तुलनाओं के लिए पी-मान देख सकते हैं:

• तकनीक 1 बनाम 2: | पी-वैल्यू = 0.024
• तकनीक 1 बनाम 3 | पी-वैल्यू = 0.883
• तकनीक 2 बनाम 3 | पी-वैल्यू = 0.067

0.05 से कम पी-मान के साथ एकमात्र समूह तुलना तकनीक 1 और तकनीक 2 के बीच है।

यह हमें बताता है कि तकनीक 1 का उपयोग करने वाले और तकनीक 2 का उपयोग करने वाले छात्रों के बीच औसत परीक्षण स्कोर में सांख्यिकीय रूप से महत्वपूर्ण अंतर है।

हालाँकि, तकनीक 1 और 3 के बीच, न ही तकनीक 2 और 3 के बीच कोई सांख्यिकीय महत्वपूर्ण अंतर नहीं है।

चरण 4: परिणामों की रिपोर्ट करें।

अंत में, हम एक-तरफ़ा एनोवा के परिणामों की रिपोर्ट कर सकते हैं। यह कैसे करें इसका एक उदाहरण यहां दिया गया है:

यह निर्धारित करने के लिए एक-तरफ़ा एनोवा का प्रदर्शन किया गया कि क्या तीन अलग-अलग अध्ययन तकनीकों के कारण अलग-अलग परीक्षण परिणाम आए।

कुल 10 छात्रों ने समान परीक्षा देने से पहले एक महीने तक तीनों अध्ययन तकनीकों में से प्रत्येक का उपयोग किया।

एक-तरफ़ा एनोवा से पता चला कि कम से कम दो समूहों (एफ(2, 27) = 4.545, पी = 0.020) के बीच परीक्षण स्कोर में सांख्यिकीय रूप से महत्वपूर्ण अंतर था।

कई तुलनाओं के लिए तुकी के परीक्षण से पता चला कि तकनीक 1 और तकनीक 2 (पी = 0.024, 95% सीआई = [-14.48, -0. 92]) का उपयोग करने वाले छात्रों के बीच औसत परीक्षण स्कोर काफी भिन्न थे।

तकनीक 1 और 3 के स्कोर (पी = 0.883) या तकनीक 2 और 3 के स्कोर (पी = 0.067) के बीच कोई सांख्यिकीय महत्वपूर्ण अंतर नहीं था।