यूनीवेरिएट या मल्टीवेरिएट विश्लेषण: क्या अंतर है?

यूनीवेरिएट विश्लेषण शब्द का तात्पर्य एक चर के विश्लेषण से है। आप इसे याद रख सकते हैं क्योंकि उपसर्ग “यूनी” का अर्थ “एक” है।

बहुभिन्नरूपी विश्लेषण शब्द का तात्पर्य एक से अधिक चर के विश्लेषण से है। आप इसे याद रख सकते हैं क्योंकि उपसर्ग “बहु” का अर्थ है “एक से अधिक।”

अविभाज्य विश्लेषण करने के तीन सामान्य तरीके हैं:

1. सारांश आँकड़े

• हम किसी चर के लिए माध्य या माध्यिका जैसी केंद्रीय प्रवृत्ति के माप की गणना कर सकते हैं।
• हम किसी चर के लिए मानक विचलन जैसे फैलाव के मापों की भी गणना कर सकते हैं।

2. आवृत्ति वितरण

• हम एक आवृत्ति वितरण बना सकते हैं, जो बताता है कि किसी चर के लिए प्रत्येक मान कितनी बार प्रकट होता है।

3. ग्राफिक्स

• हम बॉक्सप्लॉट, हिस्टोग्राम, घनत्व प्लॉट आदि जैसे ग्राफ़ बना सकते हैं। किसी चर के मानों के वितरण की कल्पना करना।

बहुभिन्नरूपी विश्लेषण करने के दो सामान्य तरीके हैं:

1. स्कैटर प्लॉट मैट्रिक्स

• हम एक स्कैटरप्लॉट मैट्रिक्स बना सकते हैं, जो हमें डेटा सेट में चर के प्रत्येक जोड़ीदार संयोजन के बीच संबंध की कल्पना करने की अनुमति देता है।

2. मशीन लर्निंग एल्गोरिदम

• हम एकाधिक रैखिक प्रतिगमन जैसे मॉडल को फिट करने के लिए एक पर्यवेक्षित शिक्षण एल्गोरिदम का उपयोग कर सकते हैं जो एकाधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को निर्धारित करता है।
• हम एक डेटा सेट में कई चर के बीच संरचना और संबंधों को एक साथ खोजने के लिए प्रमुख घटक विश्लेषण जैसे एक अप्रशिक्षित शिक्षण एल्गोरिदम का भी उपयोग कर सकते हैं।

निम्नलिखित उदाहरण दिखाते हैं कि निम्नलिखित डेटा सेट के साथ यूनीवेरिएट और मल्टीवेरिएट विश्लेषण कैसे करें:

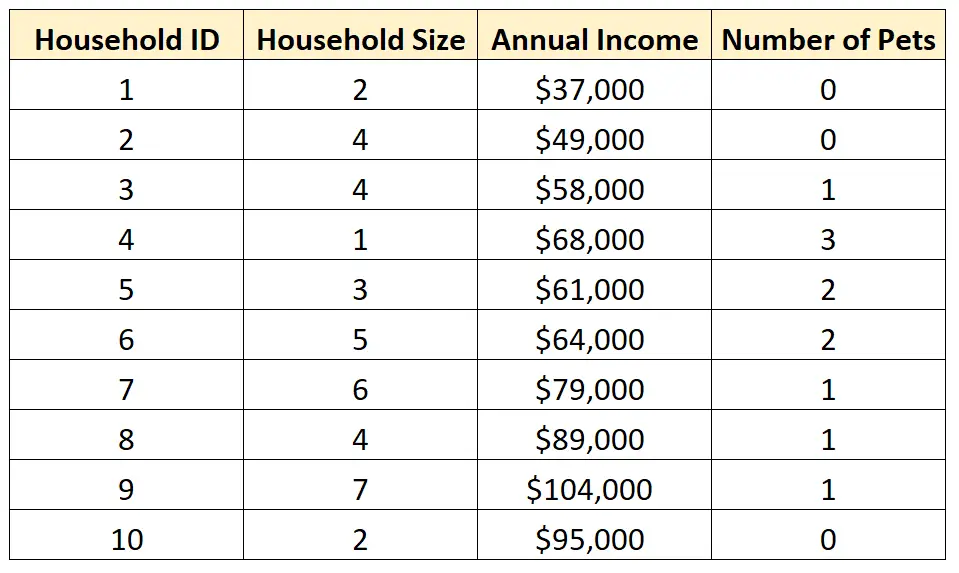
नोट : जब आप बिल्कुल दो चरों का विश्लेषण करते हैं, तो इसे द्विचर विश्लेषण कहा जाता है।

उदाहरण: यूनीवेरिएट विश्लेषण कैसे करें

हम डेटासेट में किसी भी व्यक्तिगत चर पर एक अविभाज्य विश्लेषण करना चुन सकते हैं।

उदाहरण के लिए, हम परिवर्तनीय घरेलू आकार पर एक अविभाज्य विश्लेषण करना चुन सकते हैं:

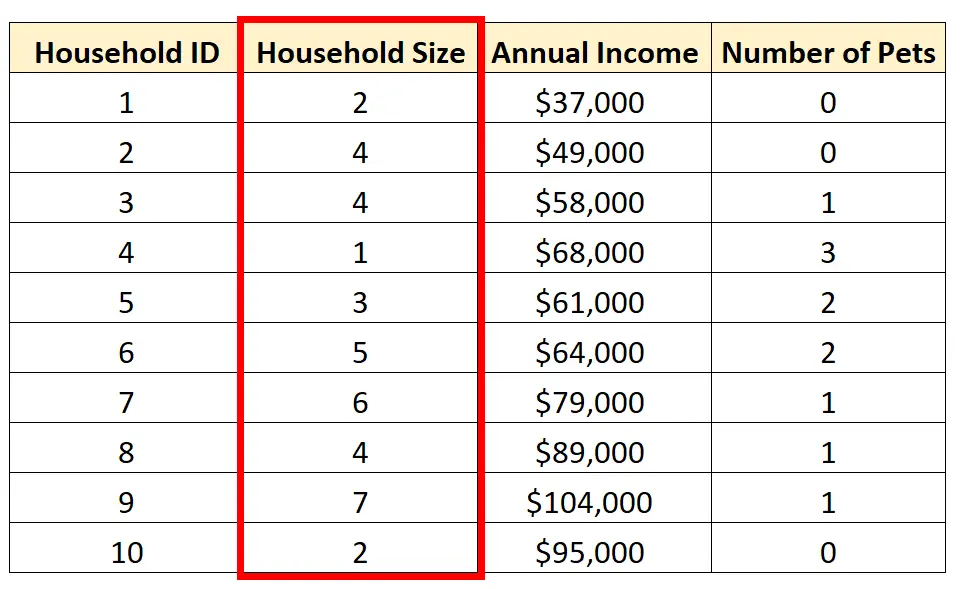
हम घरेलू आकार की केंद्रीय प्रवृत्ति के निम्नलिखित मापों की गणना कर सकते हैं:

• औसत (औसत मूल्य): 3.8
• माध्यिका (औसत मान): 4

ये मूल्य हमें यह अंदाज़ा देते हैं कि “केंद्रीय” मूल्य कहाँ निहित है।

हम निम्नलिखित फैलाव मापों की भी गणना कर सकते हैं:

• रेंज (अधिकतम और न्यूनतम के बीच का अंतर): 6
• अंतरचतुर्थक पैमाना (मध्य 50% मानों का वितरण): 2.5
• मानक विचलन (प्रसार का औसत माप): 1.87

ये मान हमें इस चर के मानों के वितरण का अंदाज़ा देते हैं।

विभिन्न मान कितनी बार आते हैं, इसका सारांश देने के लिए हम निम्नलिखित आवृत्ति वितरण तालिका भी बना सकते हैं:

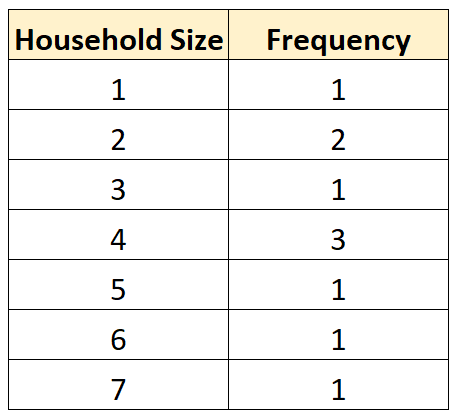
हम घरेलू आकार के अनुसार मूल्यों के वितरण की कल्पना करने के लिए एक बॉक्सप्लॉट भी बना सकते हैं:

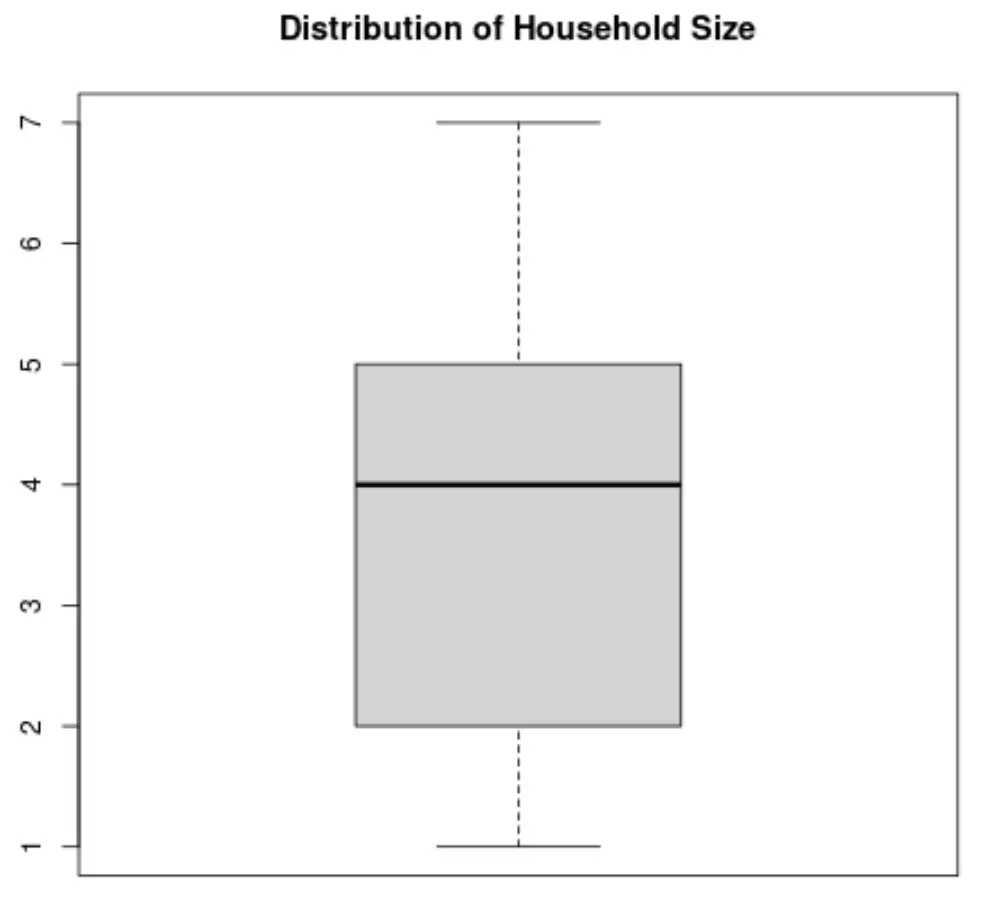
वैकल्पिक रूप से, हम मूल्यों के वितरण की कल्पना करने के लिए एक हिस्टोग्राम बना सकते हैं:

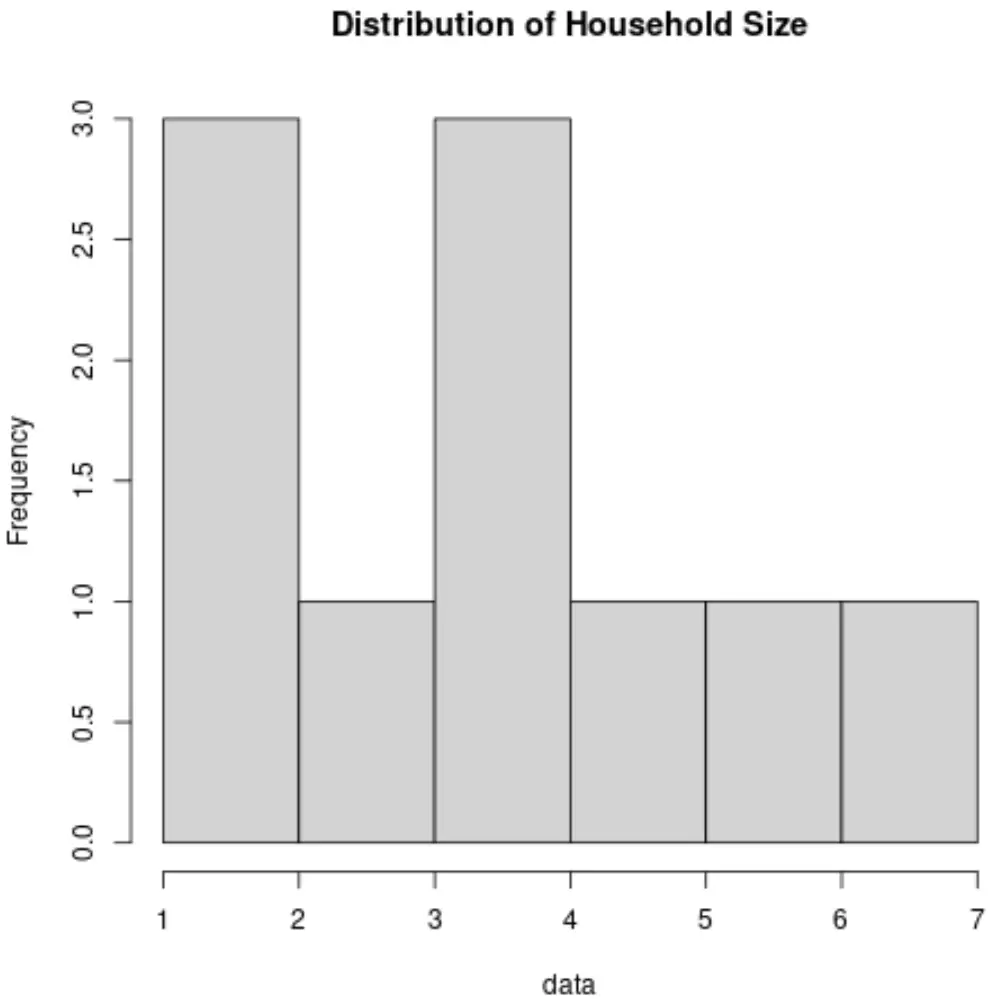
इन मापों की गणना करके और इन ग्राफ़ों को बनाकर, हम बेहतर ढंग से समझ सकते हैं कि घरेलू आकार चर के लिए मान कैसे वितरित किए जाते हैं।

उदाहरण: बहुभिन्नरूपी विश्लेषण कैसे करें

आइए फिर से मान लें कि हमारे पास समान डेटा सेट है:

बहुभिन्नरूपी विश्लेषण का एक सरल रूप जो हम इस डेटासेट पर कर सकते हैं वह एक स्कैटरप्लॉट मैट्रिक्स बनाना है, जो एक मैट्रिक्स है जो डेटासेट में संख्यात्मक चर के प्रत्येक जोड़ीदार संयोजन के लिए एक स्कैटरप्लॉट दिखाता है।

हम घर के आकार, वार्षिक आय और पालतू जानवरों की संख्या के बीच संबंधों की एक साथ कल्पना करने के लिए इस प्रकार का मैट्रिक्स बना सकते हैं।

संसाधन : आर में स्कैटरप्लॉट मैट्रिक्स कैसे बनाएं यह देखने के लिए इस ट्यूटोरियल को देखें।

इस डेटासेट पर बहुभिन्नरूपी विश्लेषण करने का दूसरा तरीका एक एकाधिक रैखिक प्रतिगमन मॉडल को फिट करना होगा। उदाहरण के लिए, हम एक प्रतिगमन मॉडल बना सकते हैं जो वार्षिक आय की भविष्यवाणी करने के लिए घरेलू आकार और पालतू जानवरों की संख्या का उपयोग करता है।

संसाधन : आर में एकाधिक रैखिक प्रतिगमन कैसे करें यह देखने के लिए इस ट्यूटोरियल को देखें।

इस डेटासेट पर बहुभिन्नरूपी विश्लेषण करने का दूसरा तरीका प्रमुख घटक विश्लेषण करना होगा, जो हमें डेटासेट में अंतर्निहित संरचना खोजने की अनुमति देता है।

संसाधन : आर में प्रमुख घटक विश्लेषण कैसे करें यह देखने के लिए इस ट्यूटोरियल को देखें।

निष्कर्ष

यहां इस लेख का संक्षिप्त सारांश दिया गया है:

• यूनीवेरिएट विश्लेषण एक चर का विश्लेषण है।
• बहुभिन्नरूपी विश्लेषण एक से अधिक चर का विश्लेषण है।
• आपके अंतिम लक्ष्य के आधार पर प्रत्येक प्रकार का विश्लेषण करने के अलग-अलग तरीके हैं।
• वास्तविक दुनिया में, हम अक्सर एक ही डेटा सेट पर दोनों प्रकार के विश्लेषण करते हैं।
• यूनीवेरिएट विश्लेषण हमें एक चर के लिए मूल्यों के वितरण को समझने की अनुमति देता है जबकि बहुभिन्नरूपी विश्लेषण हमें कई चर के बीच संबंध को समझने की अनुमति देता है।