आर गुणक या आर वर्ग: क्या अंतर है?

जब आप अधिकांश सांख्यिकीय सॉफ़्टवेयर का उपयोग करके एक प्रतिगमन मॉडल फिट करते हैं, तो आप अक्सर परिणाम में निम्नलिखित दो मान देखेंगे:

एकाधिक आर: तीन या अधिक चर के बीच एकाधिक सहसंबंध गुणांक।

आर-स्क्वायर: इसकी गणना (एकाधिक आर) ² के रूप में की जाती है और यह एक प्रतिगमन मॉडल के प्रतिक्रिया चर में भिन्नता के अनुपात का प्रतिनिधित्व करता है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है। यह मान 0 से 1 तक भिन्न होता है।

व्यवहार में, हम अक्सर आर-वर्ग मान में रुचि रखते हैं क्योंकि यह हमें बताता है कि प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने में भविष्यवक्ता चर कितने उपयोगी हैं।

हालाँकि, हर बार जब हम मॉडल में एक नया प्रेडिक्टर वेरिएबल जोड़ते हैं, तो आर-स्क्वायर बढ़ने की गारंटी होती है, भले ही प्रेडिक्टर वेरिएबल उपयोगी न हो।

समायोजित आर-स्क्वायर आर-स्क्वायर का एक संशोधित संस्करण है जो एक प्रतिगमन मॉडल में भविष्यवक्ताओं की संख्या को समायोजित करता है। इसकी गणना इस प्रकार की जाती है:

समायोजित आर ² = 1 – [(1-आर ² )*(एन-1)/(एनके-1)]

सोना:

• आर ² : मॉडल का आर ²
• n : प्रेक्षणों की संख्या
• k : भविष्यवक्ता चर की संख्या

चूँकि जब आप किसी मॉडल में अधिक भविष्यवक्ता जोड़ते हैं तो आर-वर्ग हमेशा बढ़ता है, समायोजित आर-वर्ग एक मीट्रिक के रूप में काम कर सकता है जो आपको बताता है कि एक मॉडल कितना उपयोगी है, एक मॉडल में भविष्यवक्ताओं की संख्या के आधार पर समायोजित किया जाता है।

इनमें से प्रत्येक शब्द को बेहतर ढंग से समझने के लिए, निम्नलिखित उदाहरण पर विचार करें।

उदाहरण: एकाधिक आर, आर-वर्ग और समायोजित आर-वर्ग

मान लीजिए कि हमारे पास निम्नलिखित डेटासेट है जिसमें 12 अलग-अलग छात्रों के लिए निम्नलिखित तीन चर शामिल हैं:

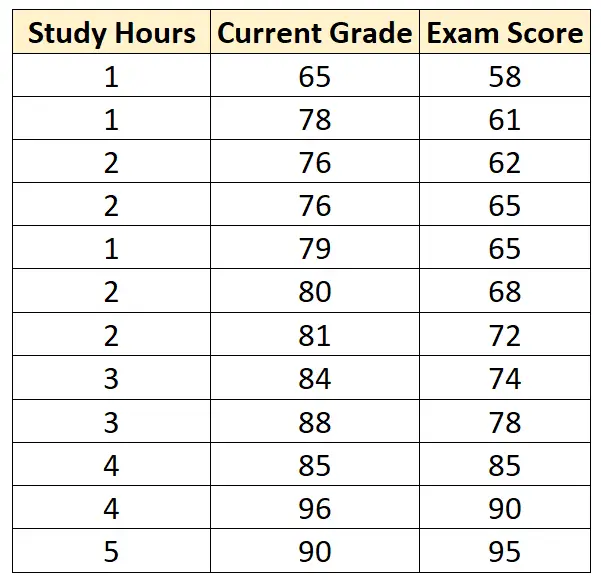
मान लीजिए कि हम भविष्यवक्ता चर के रूप में अध्ययन के घंटे और वर्तमान ग्रेड और प्रतिक्रिया चर के रूप में परीक्षा स्कोर का उपयोग करके एक बहु रेखीय प्रतिगमन मॉडल फिट करते हैं और निम्नलिखित परिणाम प्राप्त करते हैं:

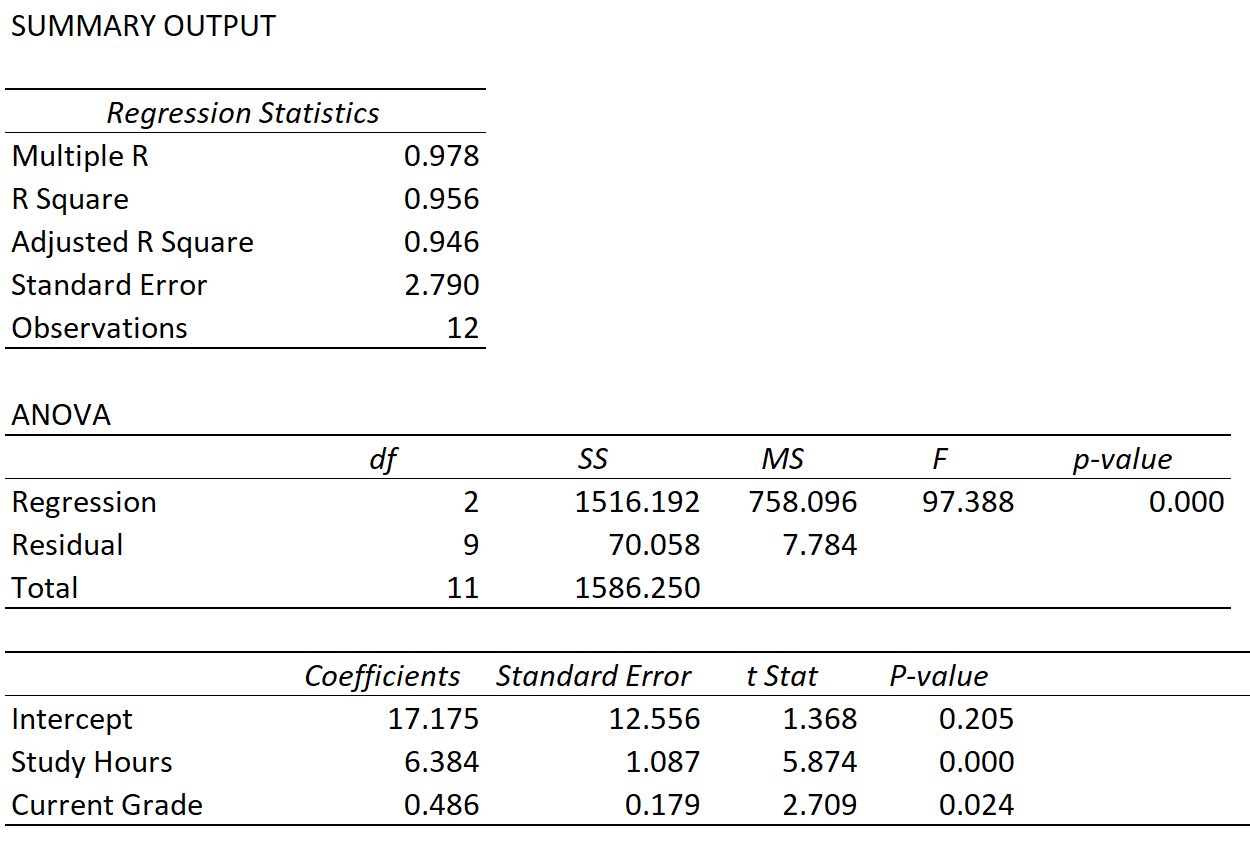
हम निम्नलिखित तीन मीट्रिक के मान देख सकते हैं:

एकाधिक आर: 0.978 । यह प्रतिक्रिया चर और दो भविष्यवक्ता चर के बीच एकाधिक सहसंबंध का प्रतिनिधित्व करता है।

आर स्क्वायर: 0.956 । इसकी गणना (एकाधिक आर) ² = (0.978) ² = 0.956 के रूप में की जाती है। यह हमें बताता है कि परीक्षा के अंकों में 95.6% भिन्नता को छात्रों द्वारा अध्ययन में बिताए गए घंटों की संख्या और पाठ्यक्रम में उनके वर्तमान ग्रेड द्वारा समझाया जा सकता है।

समायोजित आर-वर्ग: 0.946 । इसकी गणना इस प्रकार की जाती है:

समायोजित आर ² = 1 – [(1-आर ² )*(एन-1)/(एनके-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0.946.

यह आर-वर्ग मान का प्रतिनिधित्व करता है, जिसे मॉडल में भविष्यवक्ता चर की संख्या के लिए समायोजित किया गया है ।

यह माप उपयोगी होगा यदि, उदाहरण के लिए, हम 10 भविष्यवक्ताओं के साथ एक और प्रतिगमन मॉडल फिट करते हैं और पाते हैं कि उस मॉडल का समायोजित आर-वर्ग 0.88 था। यह इंगित करेगा कि केवल दो भविष्यवक्ताओं वाला प्रतिगमन मॉडल बेहतर है क्योंकि इसमें उच्च समायोजित आर वर्ग मान है।

अतिरिक्त संसाधन

एकाधिक रेखीय प्रतिगमन का परिचय
एक अच्छा आर-वर्ग मान क्या है?