एक्सेल में माध्य की मानक त्रुटि की गणना कैसे करें

माध्य की मानक त्रुटि डेटा सेट में मूल्यों के वितरण को मापने का एक तरीका है। इसकी गणना इस प्रकार की जाती है:

मानक त्रुटि = s / √n

सोना:

• s : नमूना मानक विचलन
• n : नमूना आकार

आप निम्न सूत्र का उपयोग करके एक्सेल में किसी भी डेटा सेट के माध्य की मानक त्रुटि की गणना कर सकते हैं:

= STDEV (मानों की श्रेणी) / SQRT ( COUNT (मानों की श्रेणी))

निम्नलिखित उदाहरण दिखाता है कि इस सूत्र का उपयोग कैसे करें।

उदाहरण: एक्सेल में मानक त्रुटि

मान लीजिए हमारे पास निम्नलिखित डेटा सेट है:

निम्नलिखित स्क्रीनशॉट दिखाता है कि इस डेटा सेट के लिए माध्य की मानक त्रुटि की गणना कैसे करें:

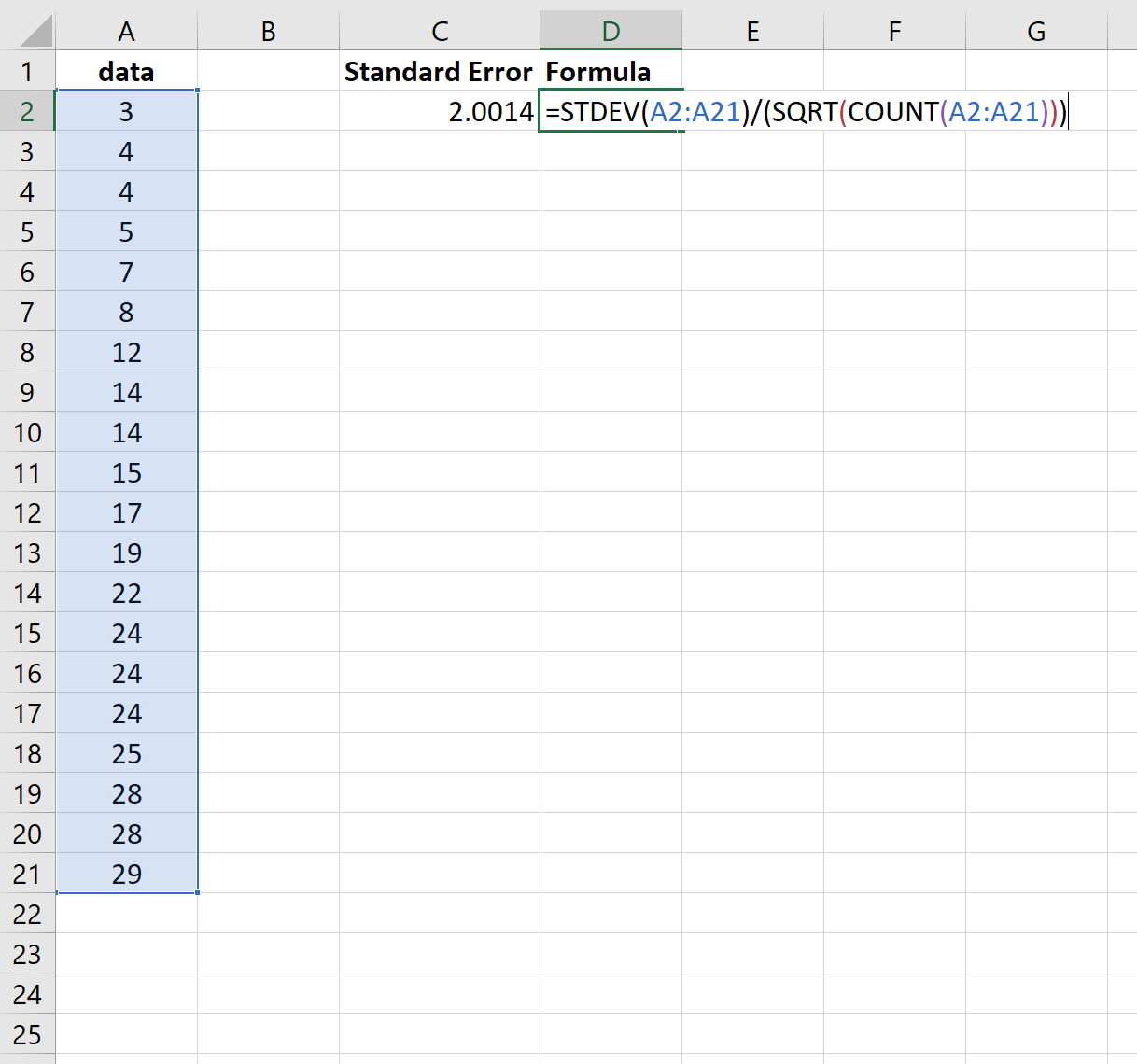
मानक त्रुटि 2.0014 निकली।

ध्यान दें कि =STDEV() फ़ंक्शन नमूना माध्य की गणना करता है, जो एक्सेल में =STDEV.S() फ़ंक्शन के बराबर है।

इसलिए, समान परिणाम प्राप्त करने के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते थे:

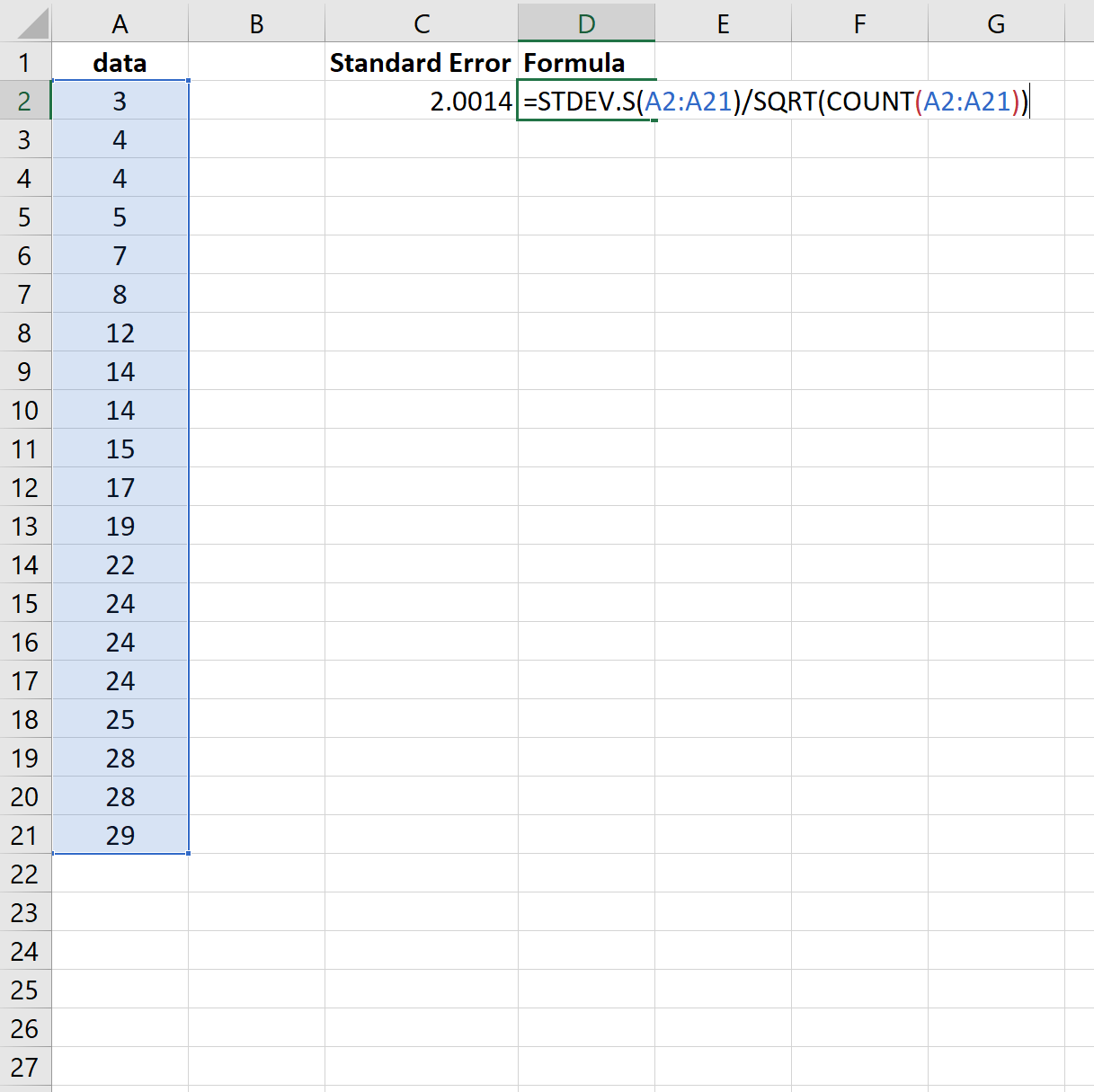
एक बार फिर, मानक त्रुटि 2.0014 निकली।

माध्य की मानक त्रुटि की व्याख्या कैसे करें

माध्य की मानक त्रुटि माध्य के चारों ओर मूल्यों के प्रसार का एक माप मात्र है। माध्य की मानक त्रुटि की व्याख्या करते समय दो बातें ध्यान में रखनी चाहिए:

1. माध्य की मानक त्रुटि जितनी बड़ी होगी, डेटा सेट में माध्य के आसपास मान उतने ही अधिक बिखरे हुए होंगे।

इसे स्पष्ट करने के लिए, विचार करें कि क्या हम पिछले डेटासेट के अंतिम मान को बहुत बड़ी संख्या से बदलते हैं:

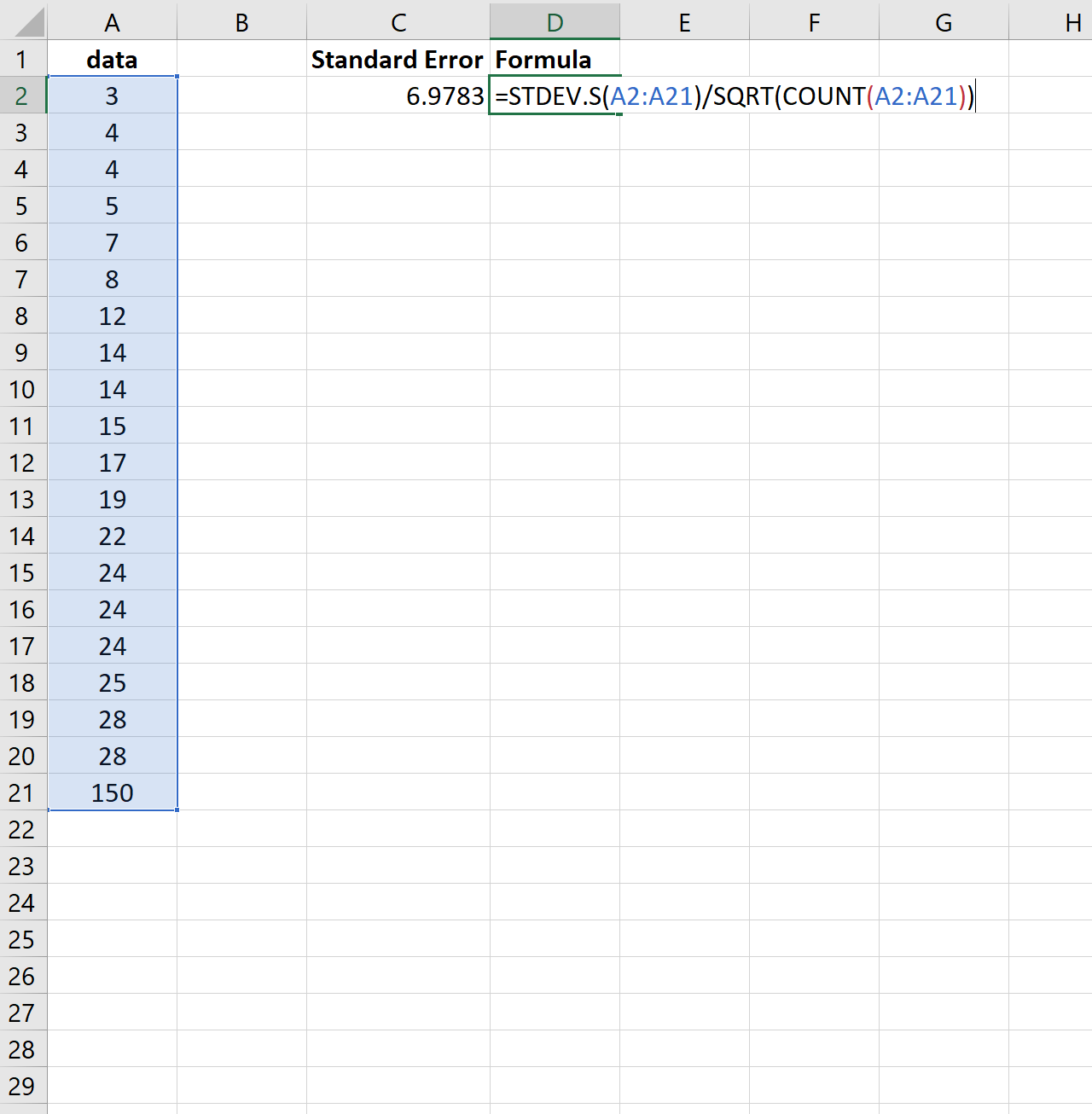
ध्यान दें कि मानक त्रुटि 2.0014 से बढ़कर 6.9783 कैसे हो जाती है। यह इंगित करता है कि इस डेटासेट में मान पिछले डेटासेट की तुलना में माध्य के आसपास अधिक वितरित हैं।

2. जैसे-जैसे नमूना आकार बढ़ता है, माध्य की मानक त्रुटि कम होती जाती है।

इसे स्पष्ट करने के लिए, डेटा के निम्नलिखित दो सेटों के लिए माध्य की मानक त्रुटि पर विचार करें:

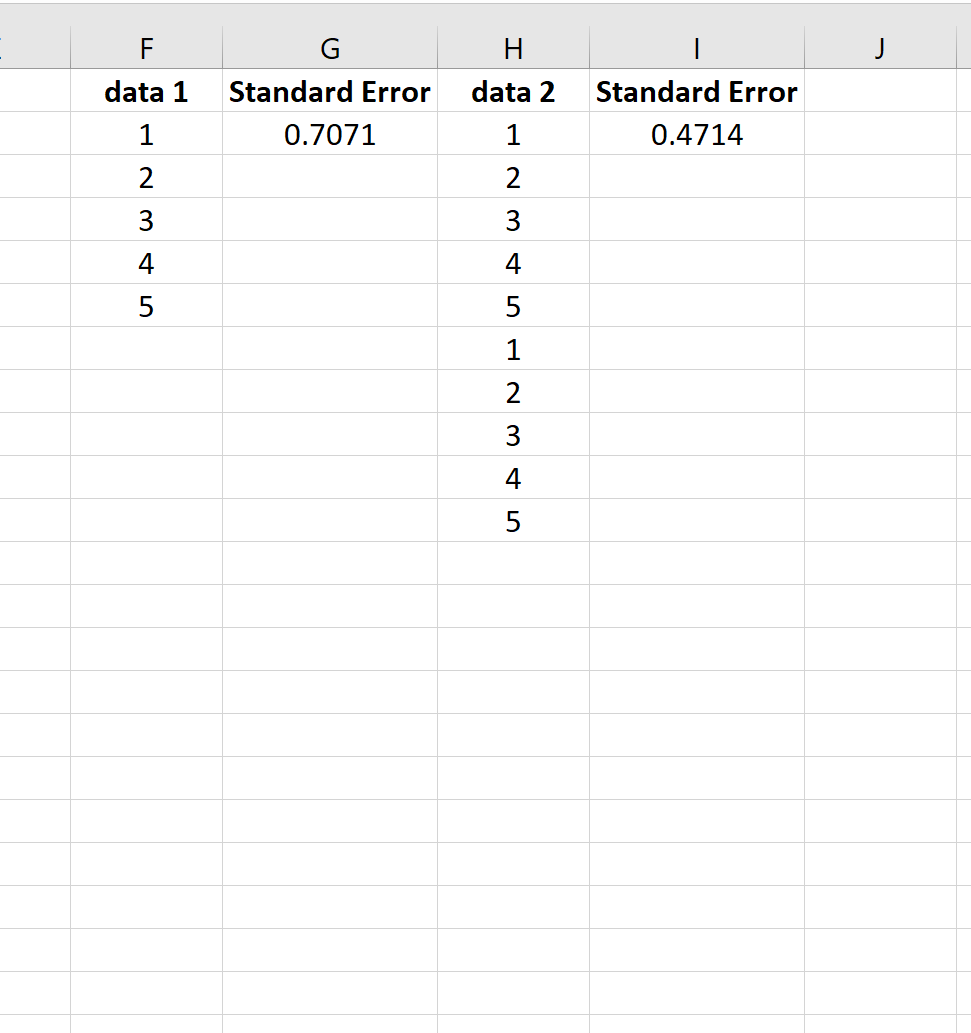
दूसरा डेटा सेट केवल पहला डेटा सेट है जिसे दो बार दोहराया गया है। इसलिए दोनों डेटा सेट का माध्य समान है लेकिन दूसरे डेटा सेट का नमूना आकार बड़ा है और इसलिए इसमें छोटी मानक त्रुटि है।