एक्सेल में पी मान की गणना कैसे करें (3 उदाहरण)

आंकड़ों में, हम यह निर्धारित करने के लिए परिकल्पना परीक्षण का उपयोग करते हैं कि जनसंख्या पैरामीटर के बारे में कोई कथन सत्य है या नहीं।

जब हम एक परिकल्पना परीक्षण करते हैं, तो हमें अक्सर एक टी-स्कोर परीक्षण आँकड़ा दिया जाता है।

एक बार जब हमें यह टी-स्कोर परीक्षण आँकड़ा मिल जाता है, तो हम इसके साथ जुड़े पी-वैल्यू का पता लगा सकते हैं।

यदि यह पी-मान एक निश्चित मान (जैसे 0.10, 0.05, 0.01) से कम है, तो हम परीक्षण की शून्य परिकल्पना को अस्वीकार करते हैं और निष्कर्ष निकालते हैं कि हमारे परिणाम सांख्यिकीय रूप से महत्वपूर्ण हैं।

निम्नलिखित उदाहरण दिखाते हैं कि एक्सेल में तीन अलग-अलग परिदृश्यों में परीक्षण आंकड़ों के लिए पी-वैल्यू की गणना कैसे करें।

उदाहरण 1: दो-पूंछ वाले परीक्षण के लिए पी मान की गणना करें

मान लीजिए कि एक वनस्पतिशास्त्री जानना चाहता है कि क्या किसी विशेष प्रजाति के पौधे की औसत ऊंचाई 15 इंच के बराबर है।

12 पौधों के एक यादृच्छिक नमूने में, उसने पाया कि नमूने की औसत ऊंचाई 14.33 इंच है और नमूने का मानक विचलन 1.37 इंच है।

यह निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करके एक परिकल्पना परीक्षण करता है:

एच ₀ (शून्य परिकल्पना): μ= 15 इंच

एच _ए (वैकल्पिक परिकल्पना): μ ≠ 15 इंच

परीक्षण आँकड़े की गणना इस प्रकार की जाती है:

• टी = ( एक्स – µ) / (एस/ √एन )
• टी = (14.33-15) / (1.37/√ 12 )
• टी = -1.694

इस परीक्षण आँकड़े से जुड़ी स्वतंत्रता की डिग्री n-1 = 12-1 = 11 है।

इस परीक्षण आँकड़े के लिए पी-मान ज्ञात करने के लिए, हम एक्सेल में निम्नलिखित सूत्र का उपयोग करेंगे:

 =T.DIST.2T(ABS(-1.694), 11)

निम्नलिखित स्क्रीनशॉट दिखाता है कि व्यवहार में इस सूत्र का उपयोग कैसे करें।

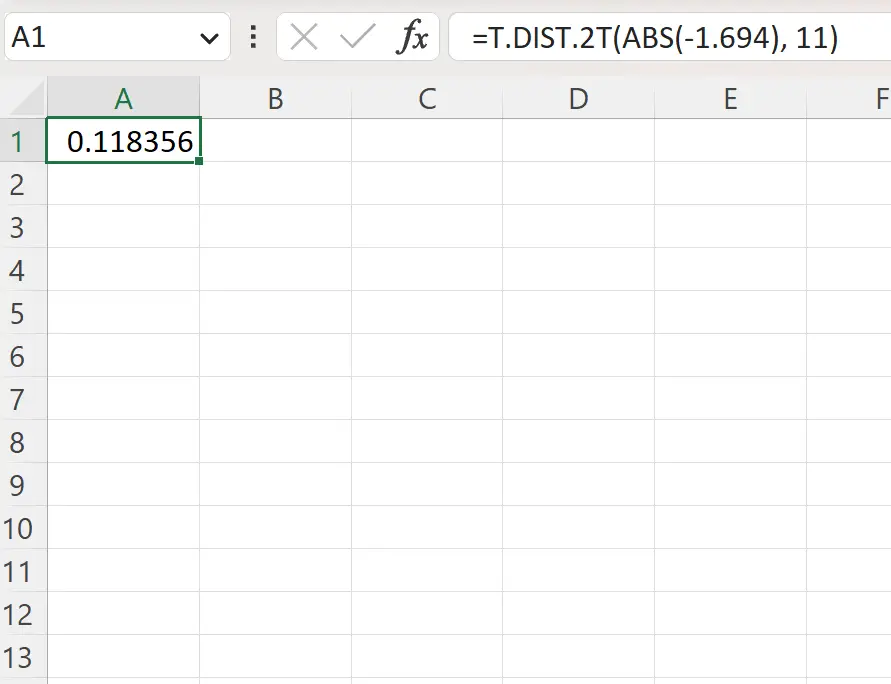
दो-पूंछ वाला पी-मान 0.1184 है।

चूँकि यह मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि पौधे की औसत ऊंचाई 15 इंच से भिन्न होती है।

उदाहरण 2: बाईं ओर परीक्षण के लिए पी मान की गणना करें

मान लीजिए हम मानते हैं कि किसी कारखाने में उत्पादित एक निश्चित गैजेट का औसत वजन 20 ग्राम है। हालाँकि, एक निरीक्षक का अनुमान है कि वास्तविक औसत वजन 20 ग्राम से कम है।

इसका परीक्षण करने के लिए, यह 20 विजेट्स के एक सरल यादृच्छिक नमूने का वजन करता है और निम्नलिखित जानकारी प्राप्त करता है:

• n = 20 विजेट
• x = 19.8 ग्राम
• एस = 3.1 ग्राम

इसके बाद यह निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करके एक परिकल्पना परीक्षण करता है:

एच ₀ (शून्य परिकल्पना): μ ≥ 20 ग्राम

एच _ए (वैकल्पिक परिकल्पना): μ <20 ग्राम

परीक्षण आँकड़े की गणना इस प्रकार की जाती है:

• टी = ( एक्स – µ) / (एस/ √एन )
• टी = (19.8-20) / (3.1/√ 20 )
• टी = -.2885

इस परीक्षण आँकड़े से जुड़ी स्वतंत्रता की डिग्री n-1 = 20-1 = 19 है।

इस परीक्षण आँकड़े के लिए पी-मान ज्ञात करने के लिए, हम एक्सेल में निम्नलिखित सूत्र का उपयोग करेंगे:

 =T.DIST(-.2885, 19, TRUE)

निम्नलिखित स्क्रीनशॉट दिखाता है कि व्यवहार में इस सूत्र का उपयोग कैसे करें।

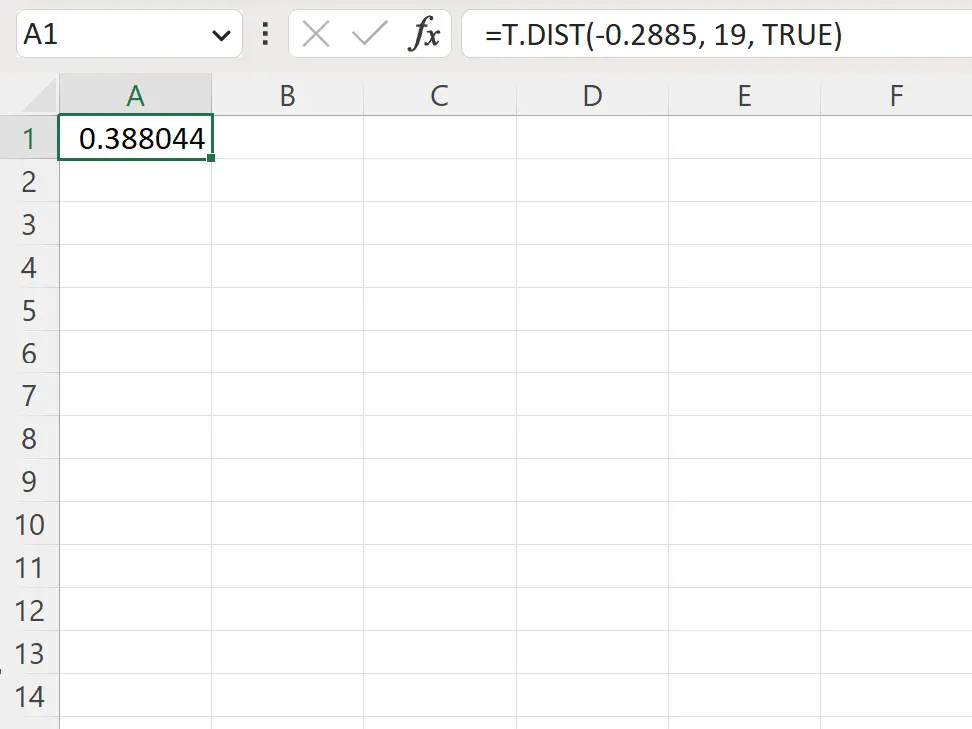
बायीं ओर पी-मान 0.388044 है।

चूँकि यह मान 0.05 से कम नहीं है, निरीक्षक शून्य परिकल्पना को अस्वीकार करने में विफल रहता है। यह कहने के लिए अपर्याप्त सबूत हैं कि इस कारखाने में उत्पादित विजेट्स का वास्तविक औसत वजन 20 ग्राम से कम है।

नोट : हमने यह निर्दिष्ट करने के लिए TRUE तर्क का उपयोग किया कि पी-वैल्यू की गणना करते समय संचयी वितरण फ़ंक्शन का उपयोग किया जाना चाहिए।

उदाहरण 3: राइट-टेल्ड परीक्षण के लिए पी मान की गणना करें

आइए मान लें कि एक निश्चित पौधे की प्रजाति की औसत ऊंचाई 10 इंच है। हालाँकि, एक वनस्पतिशास्त्री का कहना है कि वास्तविक औसत ऊँचाई 10 इंच से अधिक है।

इस दावे का परीक्षण करने के लिए, वह 15 पौधों के एक साधारण यादृच्छिक नमूने की ऊंचाई मापती है और निम्नलिखित जानकारी प्राप्त करती है:

• n = 15 पौधे
• x = 11.4 इंच
• एस = 2.5 इंच

इसके बाद यह निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करके एक परिकल्पना परीक्षण करता है:

एच ₀ (शून्य परिकल्पना): μ ≤ 10 इंच

एच _ए (वैकल्पिक परिकल्पना): μ > 10 इंच

परीक्षण आँकड़े की गणना इस प्रकार की जाती है:

• टी = ( एक्स – µ) / (एस/ √एन )
• टी = (11.4-10) / (2.5/√ 15 )
• टी = 2.1689

इस परीक्षण आँकड़े से जुड़ी स्वतंत्रता की डिग्री n-1 = 15-1 = 14 है।

इस परीक्षण आँकड़े के लिए पी-मान ज्ञात करने के लिए, हम एक्सेल में निम्नलिखित सूत्र का उपयोग करेंगे:

 =T.DIST.RT(2.1689, 14)

निम्नलिखित स्क्रीनशॉट दिखाता है कि व्यवहार में इस सूत्र का उपयोग कैसे करें।

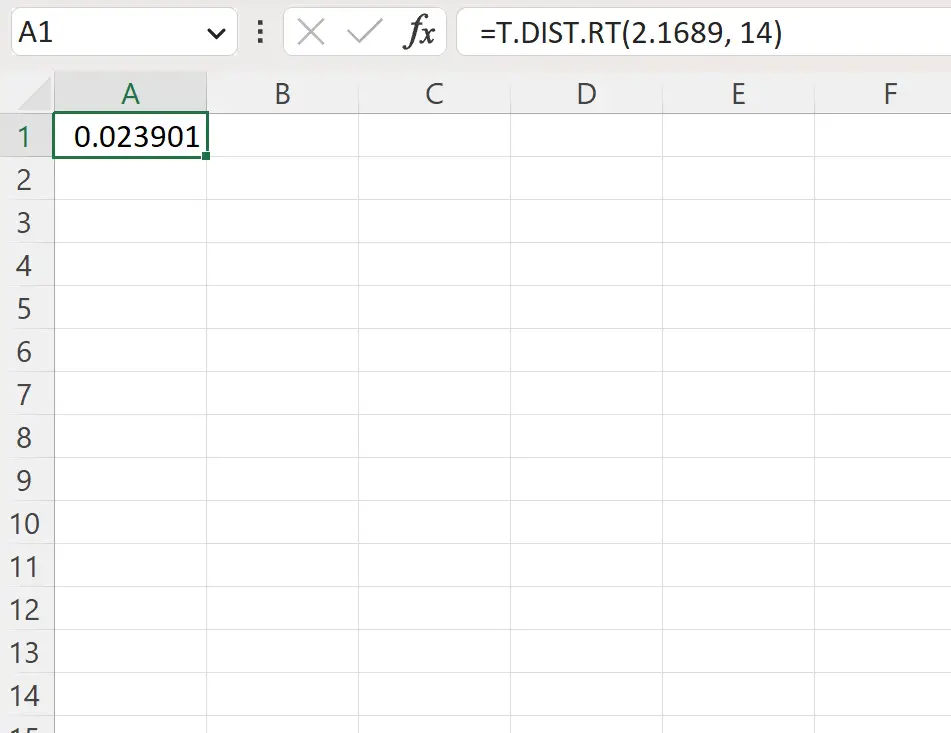
दाईं ओर पी-मान 0.023901 है।

यह मान 0.05 से कम होने के कारण वनस्पतिशास्त्री शून्य परिकल्पना को अस्वीकार कर सकता है। उनके पास यह कहने के लिए पर्याप्त सबूत हैं कि इस पौधे की प्रजाति की वास्तविक औसत ऊंचाई 10 इंच से अधिक है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एक्सेल में अन्य सामान्य कार्य कैसे करें:

Excel में Z स्कोर से P मान कैसे ज्ञात करें
Excel में किसी F आँकड़े का P मान कैसे ज्ञात करें
Excel में ची-स्क्वायर आँकड़ा का P मान कैसे ज्ञात करें