एक्सेल में नॉर्मलिटी टेस्ट कैसे करें (चरण दर चरण)

कई सांख्यिकीय परीक्षण मानते हैं कि डेटा सेट में मान सामान्य रूप से वितरित होते हैं।

इस परिकल्पना का परीक्षण करने के सबसे सरल तरीकों में से एक जर्क-बेरा परीक्षण करना है, जो एक अच्छाई-की-फिट परीक्षण है जो यह निर्धारित करता है कि नमूना डेटा सामान्य वितरण के अनुरूप तिरछापन और कर्टोसिस प्रदर्शित करता है या नहीं।

यह परीक्षण निम्नलिखित मान्यताओं का उपयोग करता है:

एच ₀ : डेटा सामान्य रूप से वितरित किया जाता है।

एच _ए : डेटा सामान्य रूप से वितरित नहीं किया जाता है।

जेबी परीक्षण आँकड़ा इस प्रकार परिभाषित किया गया है:

जेबी =(एन/6) * (एस ² + (सी ^2/4 ))

सोना:

• n: नमूने में अवलोकनों की संख्या
• एस: नमूने की विषमता
• सी: चापलूसी नमूना

सामान्यता की शून्य परिकल्पना के तहत, जेबी ~ एक्स ² (2)।

यदि परीक्षण आँकड़ों से मेल खाने वाला पी-मान एक निश्चित स्तर के महत्व से नीचे है (जैसे α = 0.05), तो हम शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि डेटा सामान्य रूप से वितरित नहीं है।

यह ट्यूटोरियल एक्सेल में दिए गए डेटा सेट के लिए जर्क-बेरा परीक्षण कैसे करें, इसका चरण-दर-चरण उदाहरण प्रदान करता है।

चरण 1: डेटा बनाएं

सबसे पहले, आइए 15 मानों वाला एक नकली डेटासेट बनाएं:

चरण 2: परीक्षण आँकड़ों की गणना करें

इसके बाद, जेबी परीक्षण आँकड़ा की गणना करें। कॉलम ई प्रयुक्त सूत्रों को दर्शाता है:

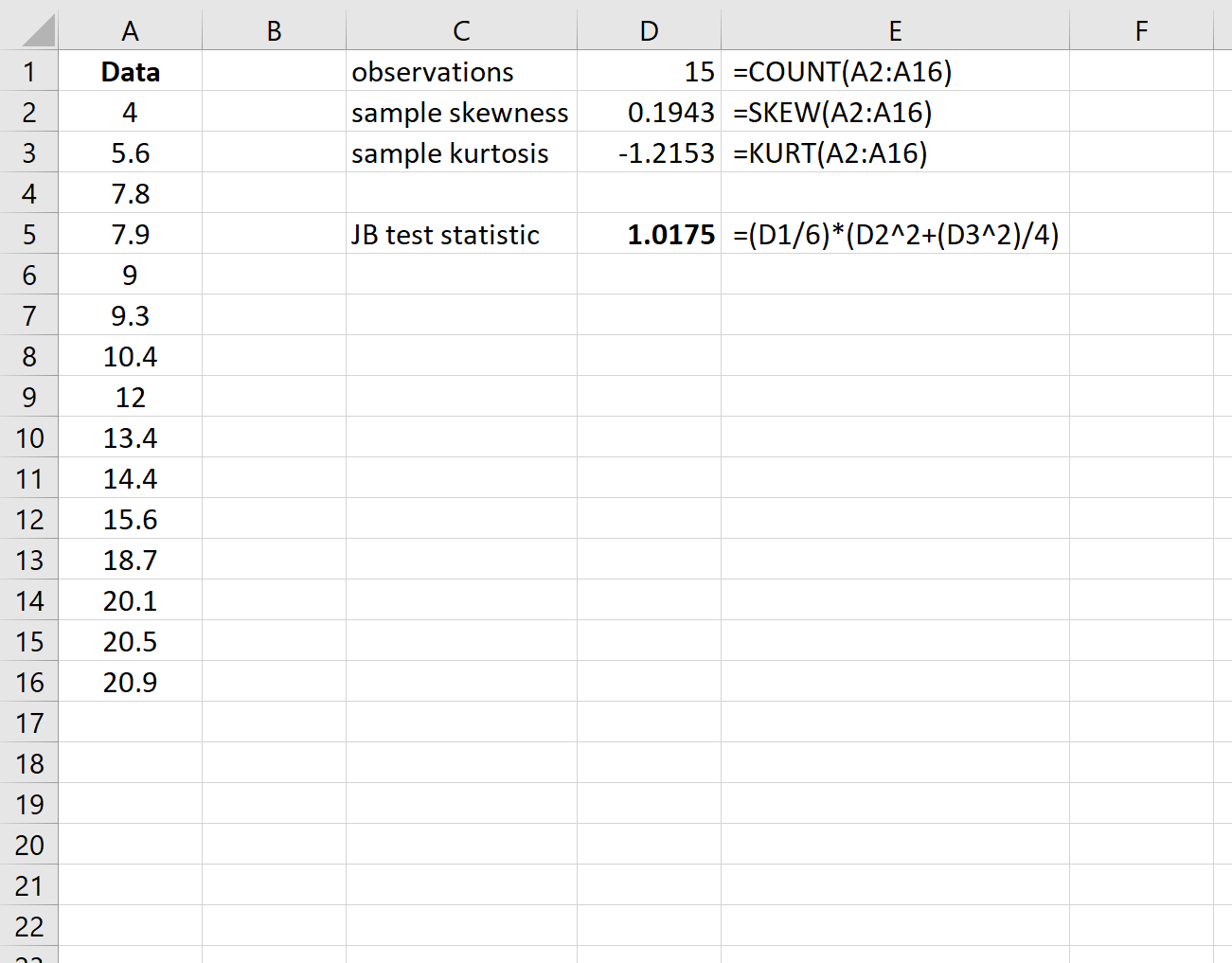
परीक्षण आँकड़ा 1.0175 निकला।

चरण 3: पी-वैल्यू की गणना करें

सामान्यता की शून्य परिकल्पना के तहत, जेबी परीक्षण आँकड़ा 2 डिग्री स्वतंत्रता के साथ ची-स्क्वायर वितरण का अनुसरण करता है।

इसलिए, परीक्षण के लिए पी-मान खोजने के लिए, हम एक्सेल में निम्नलिखित फ़ंक्शन का उपयोग करेंगे: =CHISQ.DIST.RT(JB परीक्षण आँकड़ा, 2)

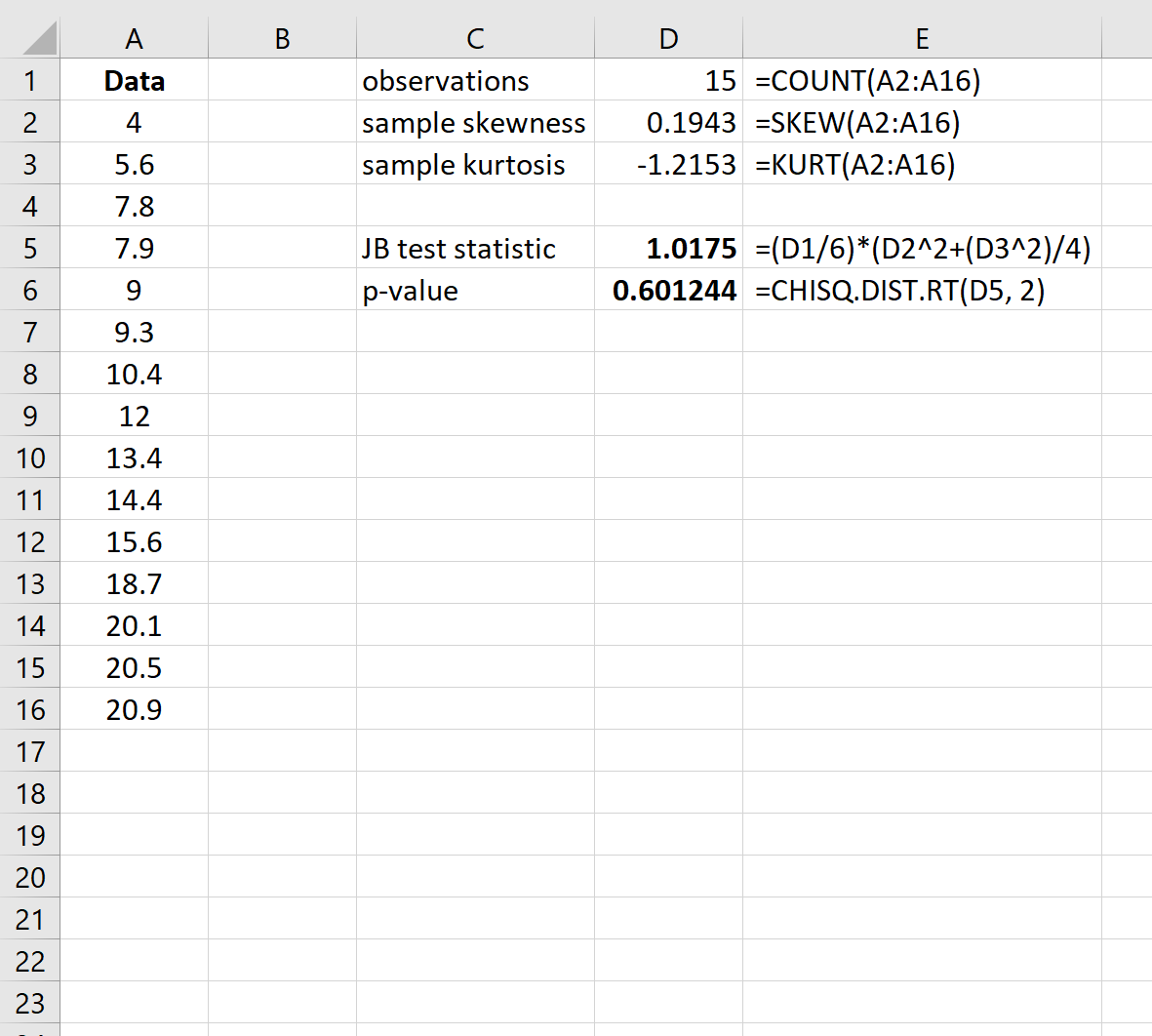
परीक्षण का पी-मान 0.601244 है। चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि डेटासेट सामान्य रूप से वितरित नहीं किया जाता है।

दूसरे शब्दों में, डेटा को सामान्य रूप से वितरित माना जा सकता है।

अतिरिक्त संसाधन

एक्सेल में QQ प्लॉट कैसे बनाएं
एक्सेल में ची स्क्वायर फ़िट टेस्ट कैसे करें