असमान नमूना आकार के साथ एनोवा कैसे निष्पादित करें

जब सांख्यिकी की बात आती है तो छात्र अक्सर एक प्रश्न पूछते हैं:

जब प्रत्येक समूह के नमूना आकार समान न हों तो क्या एक-तरफ़ा एनोवा निष्पादित करना संभव है?

संक्षिप्त उत्तर:

हाँ, जब नमूना आकार समान न हो तो आप एक-तरफ़ा एनोवा निष्पादित कर सकते हैं। समान नमूना आकार एनोवा में की गई धारणाओं में से एक नहीं है।

हालाँकि, असमान नमूना आकारों के साथ एक-तरफ़ा एनोवा का प्रदर्शन करते समय विचार करने के लिए दो संभावित मुद्दे हैं:

(1) सांख्यिकीय शक्ति में कमी।

(2) मजबूती असमान विचरण में कम हो गई।

निम्नलिखित अनुभाग इन दो संभावित मुद्दों को विस्तार से बताते हैं।

समस्या #1: सांख्यिकीय शक्ति में कमी

जब हम समूहों की तुलना करने के लिए किसी भी प्रकार के सांख्यिकीय परीक्षण का उपयोग करते हैं, तो परीक्षण की सांख्यिकीय शक्ति सबसे अधिक होती है जब प्रत्येक समूह का नमूना आकार समान होता है।

याद रखें कि सांख्यिकीय शक्ति उस संभावना को संदर्भित करती है कि एक परीक्षण एक प्रभाव का पता लगाता है जब कोई वास्तव में मौजूद होता है।

यह दिखाया जा सकता है कि समूहों के बीच नमूना आकार का अंतर जितना अधिक होगा, एनोवा की सांख्यिकीय शक्ति उतनी ही कम होगी।

यही कारण है कि शोधकर्ता आम तौर पर उच्च शक्ति के लिए समान नमूना आकार चाहते हैं और इसलिए वास्तविक मतभेदों का पता लगाने की अधिक संभावना होती है।

असमान नमूना आकारों के साथ एक-तरफ़ा एनोवा का प्रदर्शन करना निश्चित रूप से संभव है, लेकिन आपको पता होना चाहिए कि एक-तरफ़ा एनोवा की शक्ति कम हो जाएगी।

समस्या #2: मजबूती असमान विचरण में कम हो गई

एक-तरफ़ा एनोवा की धारणाओं में से एक यह है कि प्रत्येक समूह के बीच का अंतर बराबर है।

सामान्य तौर पर, एक-तरफ़ा एनोवा को समान भिन्नताओं की धारणा के उल्लंघन के लिए मजबूत माना जाता है, लेकिन केवल तभी जब प्रत्येक समूह का नमूना आकार समान हो ।

इसलिए, यदि आपके पास असमान नमूना आकार और समूहों के बीच असमान भिन्नताएं हैं, तो एक-तरफ़ा एनोवा के परिणामों पर भरोसा करना मुश्किल हो सकता है।

यह कैसे तय करें कि असमान नमूना आकारों के साथ एक-तरफ़ा एनोवा का उपयोग किया जाए या नहीं

यदि आपके पास असमान नमूना आकार हैं और समूह साधनों के बीच अंतर का परीक्षण करने के लिए एक-तरफ़ा एनोवा निष्पादित करना चाहते हैं, तो आप आगे बढ़ने का निर्णय लेने के लिए निम्नलिखित फ़्लोचार्ट का उपयोग कर सकते हैं:

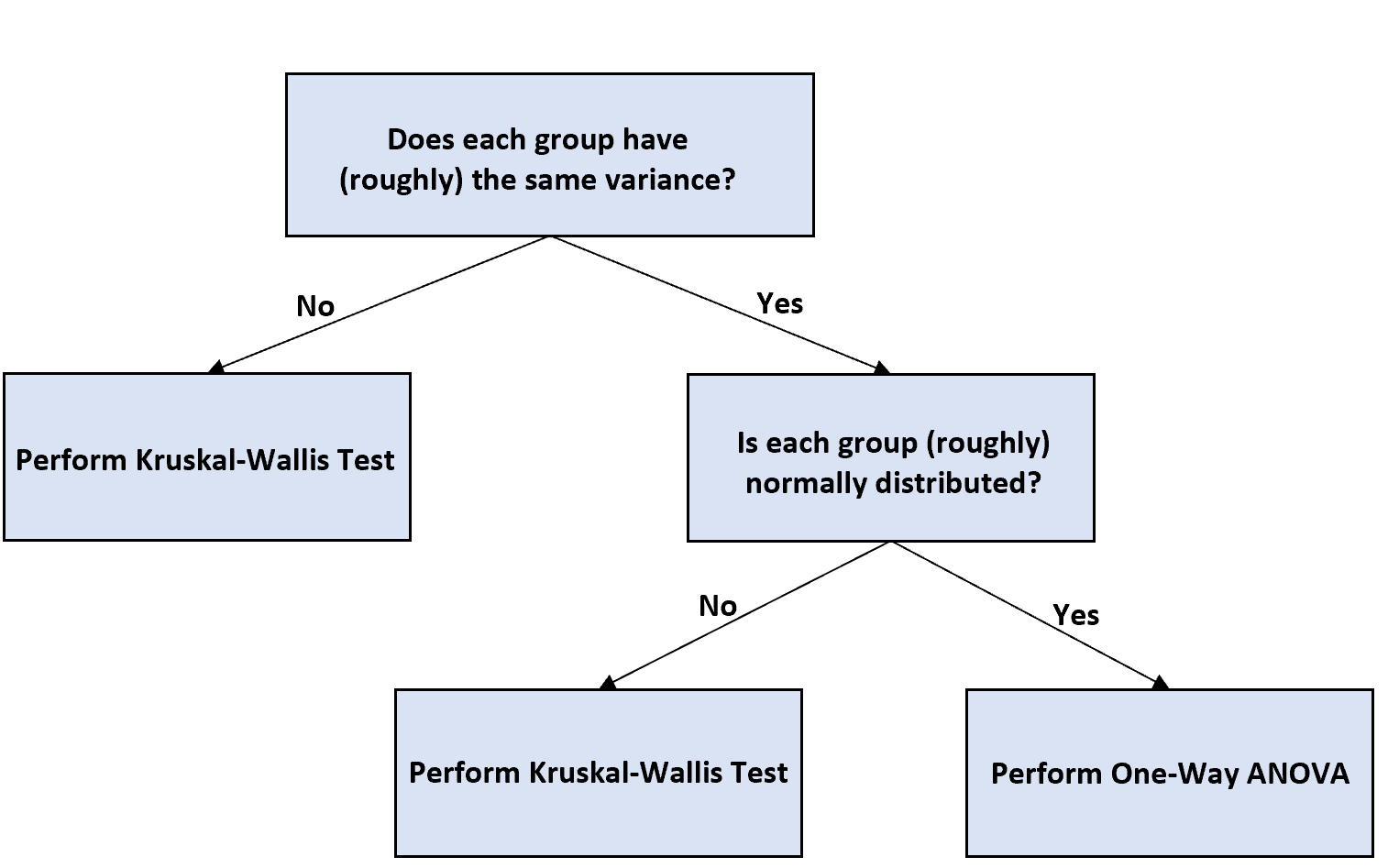
यहां फ़्लोचार्ट का संक्षिप्त विवरण दिया गया है:

चरण 1: निर्धारित करें कि क्या प्रत्येक समूह में समान भिन्नता है।

यह निर्धारित करने के लिए कि क्या प्रत्येक समूह में समान भिन्नता है, आप दो तरीकों में से एक का उपयोग कर सकते हैं:

• प्रत्येक समूह के लिए बॉक्सप्लॉट बनाएं और देखें कि क्या प्रत्येक समूह में मूल्यों का वितरण लगभग बराबर है।
• बार्टलेट परीक्षण की तरह समान भिन्नताओं के लिए एक औपचारिक सांख्यिकीय परीक्षण करें।

यदि भिन्नताएँ समान नहीं हैं, तो क्रुस्कल-वालिस परीक्षण करें, जिसे एक-तरफ़ा एनोवा के गैर-पैरामीट्रिक समकक्ष माना जाता है।

यदि अंतराल बराबर हैं, तो अगले चरण पर आगे बढ़ें।

चरण 2: निर्धारित करें कि क्या प्रत्येक समूह सामान्य रूप से वितरित है।

यह निर्धारित करने के लिए कि क्या प्रत्येक समूह में मान लगभग सामान्य रूप से वितरित हैं, आप दो तरीकों में से एक का उपयोग कर सकते हैं:

• प्रत्येक समूह के लिए हिस्टोग्राम या QQ प्लॉट बनाएं।
• शापिरो-विल्क, कोलमोगोरोव-स्मिरोनोव, जार्के-बैरे, या डी’ऑगोस्टिनो-पियर्सन जैसे औपचारिक सांख्यिकीय परीक्षण करें।

यदि प्रत्येक समूह को सामान्य रूप से वितरित किया जाता है, तो आप एक-तरफ़ा एनोवा का संचालन कर सकते हैं और परिणामों की व्याख्या कर सकते हैं जैसे कि आप किसी भी सामान्य एक-तरफ़ा एनोवा की तरह करते हैं।

यदि प्रत्येक समूह सामान्य रूप से वितरित नहीं है, तो इसके बजाय क्रुस्कल-वालिस परीक्षण करें।

अतिरिक्त संसाधन

वन-वे एनोवा का परिचय
एनोवा मान्यताओं की जांच कैसे करें
क्रुस्कल-वालिस परीक्षण का परिचय
एनोवा में एफ मान और पी मान की व्याख्या कैसे करें