एनोवा बनाम प्रतिगमन: क्या अंतर है?
सांख्यिकी में आमतौर पर उपयोग किए जाने वाले दो मॉडल एनोवा और रिग्रेशन मॉडल हैं।
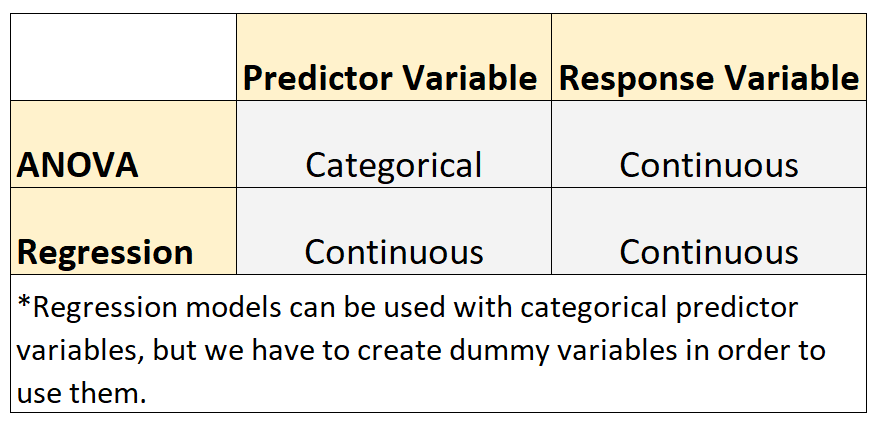
ये दो प्रकार के मॉडल निम्नलिखित समानता साझा करते हैं:
- प्रत्येक मॉडल में प्रतिक्रिया चर निरंतर है। सतत चर के उदाहरणों में वजन, ऊंचाई, लंबाई, चौड़ाई, समय, आयु आदि शामिल हैं।
हालाँकि, ये दो प्रकार के मॉडल निम्नलिखित अंतर साझा करते हैं:
- एनोवा मॉडल का उपयोग तब किया जाता है जब भविष्यवक्ता चर श्रेणीबद्ध होते हैं। श्रेणीबद्ध चर के उदाहरणों में शिक्षा स्तर, आंखों का रंग, वैवाहिक स्थिति आदि शामिल हैं।
- प्रतिगमन मॉडल का उपयोग तब किया जाता है जब भविष्यवक्ता चर निरंतर होते हैं।*
*प्रतिगमन मॉडल का उपयोग श्रेणीबद्ध भविष्यवक्ता चर के साथ किया जा सकता है, लेकिन हमें उनका उपयोग करने के लिए डमी चर बनाने की आवश्यकता है।
निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में एनोवा या प्रतिगमन मॉडल का उपयोग कब करना है।
उदाहरण 1: पसंदीदा एनोवा मॉडल
मान लीजिए कि एक जीवविज्ञानी यह समझना चाहता है कि क्या चार अलग-अलग उर्वरकों से एक महीने की अवधि में समान औसत पौधे की वृद्धि (इंच में) होती है या नहीं। इसका परीक्षण करने के लिए, वह प्रत्येक उर्वरक को 20 पौधों पर लगाती है और एक महीने के बाद प्रत्येक पौधे की वृद्धि को रिकॉर्ड करती है।
इस परिदृश्य में, जीवविज्ञानी को उर्वरकों के बीच अंतर का विश्लेषण करने के लिए एक-तरफ़ा एनोवा मॉडल का उपयोग करना चाहिए क्योंकि एक भविष्यवक्ता चर है और यह श्रेणीबद्ध है।
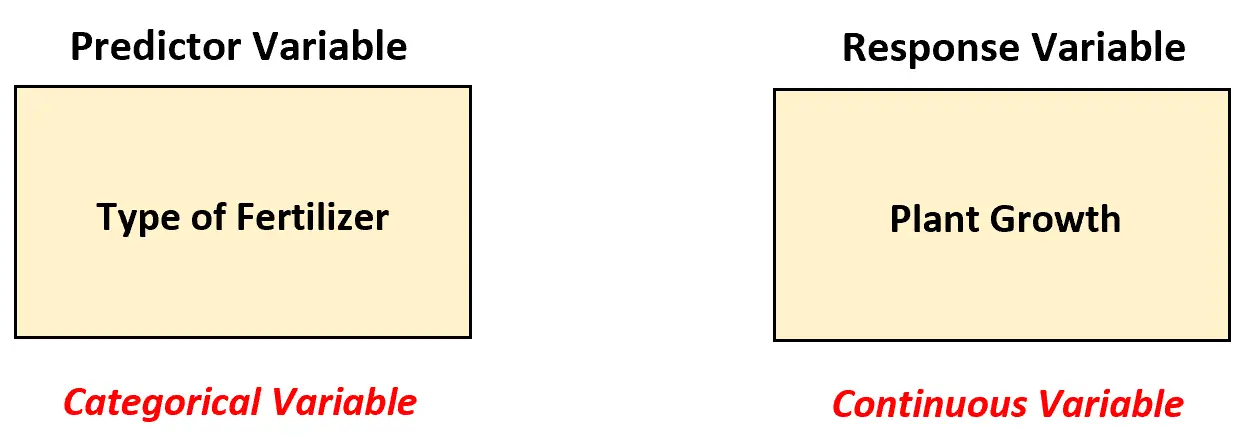
दूसरे शब्दों में, भविष्यवक्ता चर के मूल्यों को निम्नलिखित “श्रेणियों” में वर्गीकृत किया जा सकता है:
- उर्वरक 1
- उर्वरक 2
- उर्वरक 3
- उर्वरक 4
एकतरफ़ा एनोवा जीवविज्ञानी को बताएगा कि चार अलग-अलग उर्वरकों के बीच पौधों की औसत वृद्धि बराबर है या नहीं।
उदाहरण 2: पसंदीदा प्रतिगमन मॉडल
मान लीजिए कि एक रियल एस्टेट एजेंट वर्ग फुटेज और रियल एस्टेट कीमत के बीच संबंध को समझना चाहता है। इस संबंध का विश्लेषण करने के लिए, वह एक विशेष शहर में 200 घरों के वर्ग फुटेज और कीमत पर डेटा एकत्र करता है।
इस परिदृश्य में, रियल एस्टेट एजेंट को इन दो चर के बीच संबंध का विश्लेषण करने के लिए एक सरल रैखिक प्रतिगमन मॉडल का उपयोग करना चाहिए क्योंकि भविष्यवक्ता चर (वर्ग फुटेज) निरंतर है।
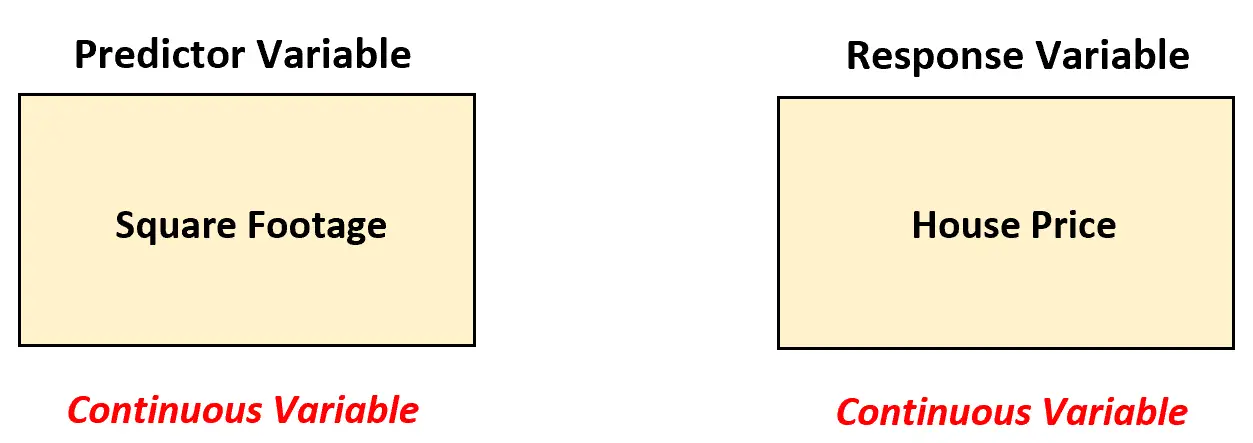
सरल रैखिक प्रतिगमन का उपयोग करके, रियल एस्टेट एजेंट निम्नलिखित प्रतिगमन मॉडल को फिट कर सकता है:
अचल संपत्ति की कीमत = β 0 + β 1 (वर्ग क्षेत्रफल)
β 1 का मान प्रत्येक अतिरिक्त वर्ग फुट से जुड़े घर की कीमत में औसत परिवर्तन का प्रतिनिधित्व करेगा।
यह रियल एस्टेट एजेंट को वर्ग फुटेज और संपत्ति की कीमत के बीच संबंध को मापने की अनुमति देगा।
उदाहरण 3: पसंदीदा डमी चर के साथ प्रतिगमन मॉडल
मान लीजिए कि एक रियल एस्टेट एजेंट रियल एस्टेट मूल्य के प्रतिक्रिया चर के साथ भविष्यवक्ता चर “स्क्वायर फुटेज” और “घर का प्रकार” (एकल परिवार, अपार्टमेंट, टाउनहाउस) के बीच संबंध को समझना चाहता है।
इस परिदृश्य में, रियल एस्टेट एजेंट “होम टाइप” को एक डमी वैरिएबल में परिवर्तित करके एकाधिक रैखिक प्रतिगमन का उपयोग कर सकता है क्योंकि यह वर्तमान में एक श्रेणीगत वैरिएबल है।
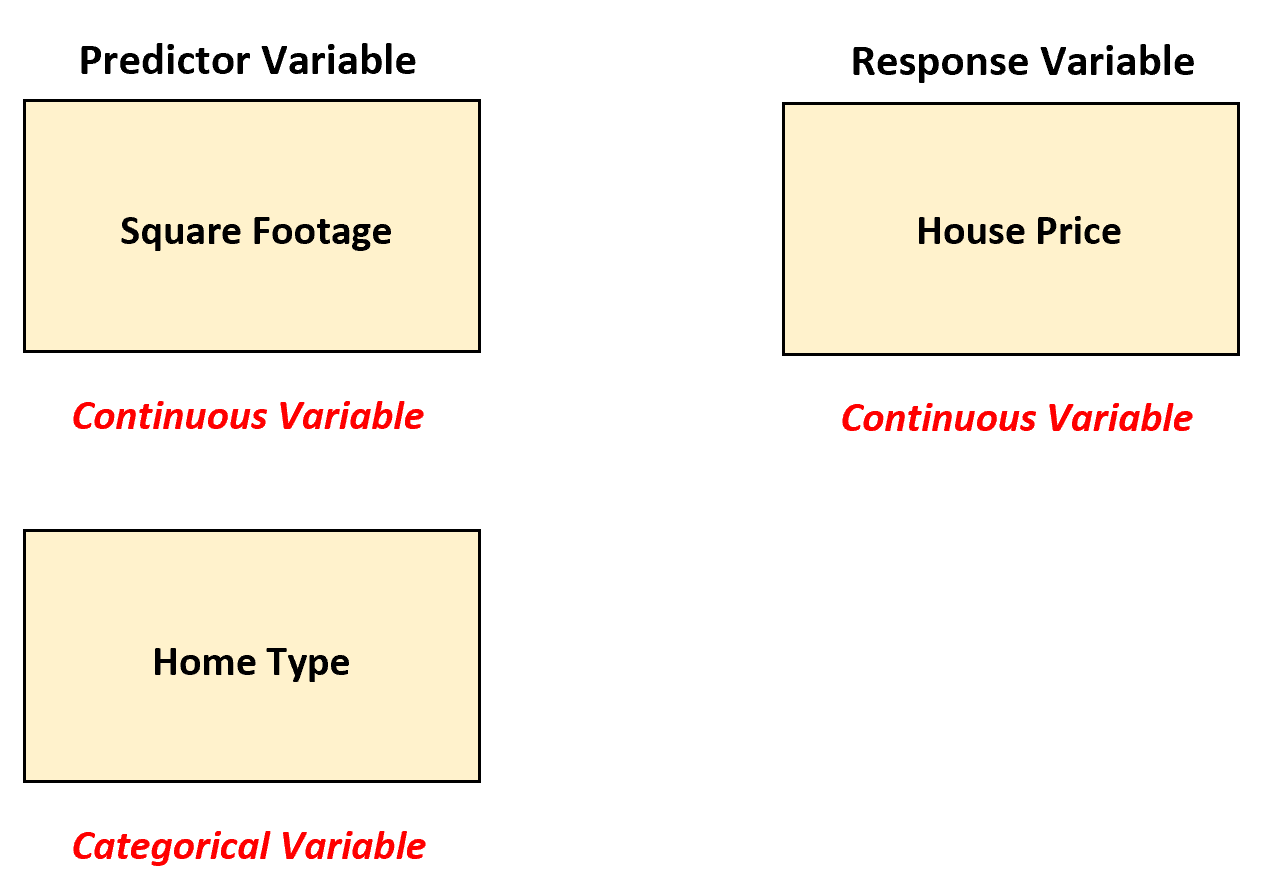
रियल एस्टेट एजेंट निम्नलिखित एकाधिक रैखिक प्रतिगमन मॉडल को फिट कर सकता है:
अचल संपत्ति की कीमत = β 0 + β 1 (वर्ग क्षेत्र) + β 2 (एकल परिवार) + β 3 (अपार्टमेंट)
यहां बताया गया है कि हम मॉडल गुणांक की व्याख्या कैसे करेंगे:
- β 1 : एक अतिरिक्त वर्ग फुट से जुड़े घर की कीमत में औसत परिवर्तन।
- β 2 : एकल-परिवार के घर और टाउनहाउस के बीच औसत मूल्य अंतर, वर्ग फुटेज मानते हुए स्थिर रहता है।
- β 3 : एक स्थिर सतह क्षेत्र मानते हुए, एकल-परिवार के घर और एक अपार्टमेंट के बीच औसत मूल्य अंतर।
विभिन्न सांख्यिकीय सॉफ़्टवेयर में डमी वैरिएबल कैसे बनाएं, यह देखने के लिए निम्नलिखित ट्यूटोरियल देखें:
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल एनोवा मॉडल का गहन परिचय प्रदान करते हैं:
निम्नलिखित ट्यूटोरियल रैखिक प्रतिगमन मॉडल का गहन परिचय प्रदान करते हैं:
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने