एमएई बनाम आरएमएसई: आपको किस मीट्रिक का उपयोग करना चाहिए?

प्रतिगमन मॉडल का उपयोग एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए किया जाता है।

जब भी हम एक प्रतिगमन मॉडल को फिट करते हैं, तो हम यह समझना चाहते हैं कि मॉडल प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए भविष्यवक्ता चर के मूल्यों का कितनी अच्छी तरह उपयोग करने में सक्षम है।

दो मीट्रिक जो हम अक्सर यह निर्धारित करने के लिए उपयोग करते हैं कि कोई मॉडल किसी डेटा सेट में कितनी अच्छी तरह फिट बैठता है, माध्य निरपेक्ष त्रुटि (MAE) और मूल माध्य वर्ग त्रुटि (RMSE) हैं, जिनकी गणना निम्नानुसार की जाती है:

एमएई : एक मीट्रिक जो हमें डेटा सेट में अनुमानित मूल्यों और वास्तविक मूल्यों के बीच औसत पूर्ण अंतर बताता है। एमएई जितना कम होगा, मॉडल डेटा सेट में उतना ही बेहतर फिट होगा।

MAE = 1/n * Σ|y _i – ŷ _i |

सोना:

• Σ एक प्रतीक है जिसका अर्थ है “योग”
• y _i, ^iवें अवलोकन के लिए प्रेक्षित मान है
• ŷ _i, i ^वें अवलोकन के लिए अनुमानित मान है
• n नमूना आकार है

आरएमएसई : एक मीट्रिक जो हमें डेटा सेट में अनुमानित मूल्यों और वास्तविक मूल्यों के बीच मूल माध्य वर्ग अंतर का वर्गमूल बताता है। आरएमएसई जितना कम होगा, मॉडल डेटा सेट में उतना ही बेहतर फिट होगा।

इसकी गणना इस प्रकार की जाती है:

आरएमएसई = √ Σ(y _i – ŷ _i ) ² / n

सोना:

• Σ एक प्रतीक है जिसका अर्थ है “योग”
• ŷ _i, i ^वें अवलोकन के लिए अनुमानित मान है
• y _i, ^iवें अवलोकन के लिए प्रेक्षित मान है
• n नमूना आकार है

उदाहरण: आरएमएसई और एमएई की गणना

मान लीजिए कि हम एक प्रतिगमन मॉडल का उपयोग यह अनुमान लगाने के लिए करते हैं कि बास्केटबॉल खेल में 10 खिलाड़ी कितने अंक अर्जित करेंगे।

निम्न तालिका खिलाड़ियों द्वारा प्राप्त वास्तविक अंकों की तुलना में मॉडल द्वारा अनुमानित अंकों को दर्शाती है:

एमएई कैलकुलेटर का उपयोग करके, हम गणना कर सकते हैं कि एमएई 3.2 है।

यह हमें बताता है कि मॉडल द्वारा अनुमानित मूल्यों और वास्तविक मूल्यों के बीच औसत पूर्ण अंतर 3.2 है।

आरएमएसई कैलकुलेटर का उपयोग करके, हम गणना कर सकते हैं कि आरएमएसई 4 के बराबर है।

यह हमें बताता है कि अनुमानित प्राप्त अंकों और वास्तविक प्राप्त अंकों के बीच मूल माध्य वर्ग अंतर का वर्गमूल 4 है।

ध्यान दें कि प्रत्येक मीट्रिक हमें मॉडल द्वारा किए गए अनुमानित मूल्य और डेटासेट में वास्तविक मूल्य के बीच विशिष्ट अंतर का एक विचार देता है, लेकिन प्रत्येक मीट्रिक की व्याख्या थोड़ी अलग होती है।

आरएमएसई बनाम एमएई: आपको किस मीट्रिक का उपयोग करना चाहिए?

यदि आप उन प्रेक्षणों को अधिक महत्व देना चाहते हैं जो माध्य से दूर हैं (अर्थात यदि 20 का विचलन 10 के विचलन से दोगुने से अधिक बुरा है), तो त्रुटि मापने के लिए आरएमएसई का उपयोग करना बेहतर है, क्योंकि आरएमएसई है माध्य से आगे के अवलोकनों के प्रति अधिक संवेदनशील।

हालाँकि, यदि 20 पर “ऑफ़सेट” होना 10 पर “ऑफ़सेट” होने से दोगुना बुरा है तो एमएई का उपयोग करना बेहतर है।

इसे स्पष्ट करने के लिए, मान लीजिए कि हमारे पास एक ऐसा खिलाड़ी है जो अंकों की संख्या के मामले में स्पष्ट रूप से सबसे आगे है:

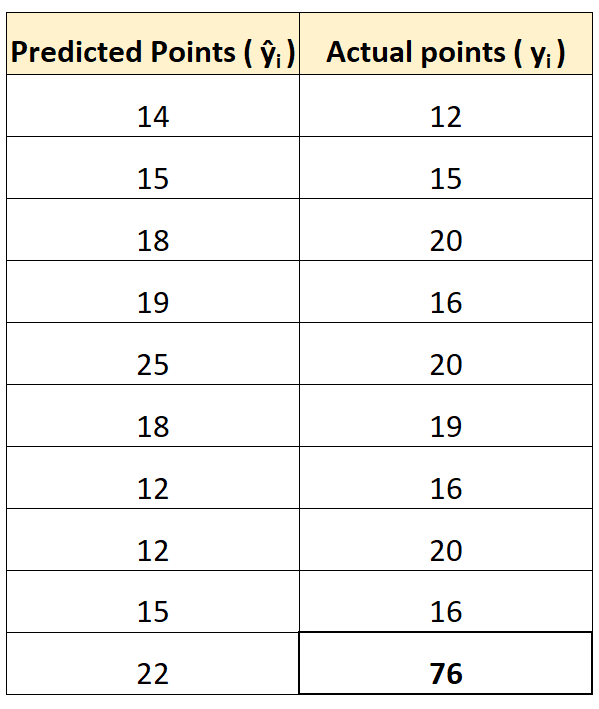
पहले बताए गए ऑनलाइन कैलकुलेटर का उपयोग करके, हम एमएई और आरएमएसई की गणना इस प्रकार कर सकते हैं:

• एमएई : 8
• आरएमएसई : 16.4356

ध्यान दें कि आरएमएसई एमएई से कहीं अधिक बढ़ता है।

ऐसा इसलिए है क्योंकि आरएमएसई अपने सूत्र में वर्ग अंतर का उपयोग करता है और 76 के देखे गए मान और 22 के अनुमानित मूल्य के बीच वर्ग अंतर काफी बड़ा है। इसके परिणामस्वरूप आरएमएसई मूल्य में उल्लेखनीय वृद्धि हुई है।

व्यवहार में, हम आम तौर पर एक डेटासेट में एकाधिक प्रतिगमन मॉडल फिट करते हैं और प्रत्येक मॉडल के लिए इनमें से केवल एक मीट्रिक की गणना करते हैं।

उदाहरण के लिए, हम तीन अलग-अलग प्रतिगमन मॉडल फिट कर सकते हैं और प्रत्येक मॉडल के लिए आरएमएसई की गणना कर सकते हैं। फिर हम सबसे कम RMSE मान वाले मॉडल को “सर्वश्रेष्ठ” मॉडल के रूप में चुनेंगे, क्योंकि यह वह है जो भविष्यवाणियों को डेटासेट में वास्तविक मूल्यों के सबसे करीब बनाता है।

किसी भी स्थिति में, बस यह सुनिश्चित करें कि आप प्रत्येक मॉडल के लिए समान मीट्रिक की गणना करें। उदाहरण के लिए, एक मॉडल के लिए एमएई और दूसरे मॉडल के लिए आरएमएसई की गणना न करें और फिर इन दोनों मापों की तुलना करें।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके एमएई की गणना कैसे करें:

एक्सेल में माध्य निरपेक्ष त्रुटि की गणना कैसे करें
आर में माध्य निरपेक्ष त्रुटि की गणना कैसे करें
पायथन में माध्य निरपेक्ष त्रुटि की गणना कैसे करें

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके आरएमएसई की गणना कैसे करें:

एक्सेल में माध्य वर्ग त्रुटि की गणना कैसे करें
आर में माध्य वर्ग त्रुटि की गणना कैसे करें
पायथन में माध्य वर्ग त्रुटि की गणना कैसे करें