एसएएस में कुक दूरी की गणना कैसे करें

कुक की दूरी का उपयोग प्रतिगमन मॉडल में प्रभावशाली अवलोकनों की पहचान करने के लिए किया जाता है।

कुक की दूरी का सूत्र है:

डी _आई = (आर _आई ² / पी*एमएसई) * (एच _II / (1-एच _II ) ² )

सोना:

• आर _मैं मैं ^वें अवशेष है
• p प्रतिगमन मॉडल में गुणांकों की संख्या है
• एमएसई माध्य वर्ग त्रुटि है
• h _ii ^ith उत्तोलन मान है

अनिवार्य रूप से, कुक की दूरी मापती है कि i ^वें अवलोकन को हटा दिए जाने पर मॉडल के सभी फिट किए गए मान कितने बदल जाते हैं।

कुक की दूरी का मान जितना बड़ा होगा, दिया गया अवलोकन उतना ही अधिक प्रभावशाली होगा।

आम तौर पर, 4/एन (जहां एन = कुल अवलोकन) से अधिक कुक दूरी वाले किसी भी अवलोकन को बड़ा प्रभाव माना जाता है।

निम्नलिखित उदाहरण दिखाता है कि एसएएस में प्रतिगमन मॉडल में प्रत्येक अवलोकन के लिए कुक की दूरी की गणना कैसे करें।

उदाहरण: एसएएस में रसोइया की दूरी की गणना

आइए मान लें कि हमारे पास एसएएस में निम्नलिखित डेटा सेट है:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

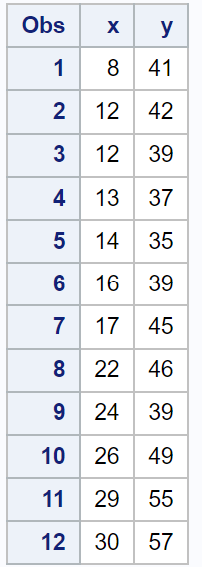
हम इस डेटा सेट में एक सरल रैखिक प्रतिगमन मॉडल को फिट करने के लिए PROC REG का उपयोग कर सकते हैं, फिर प्रतिगमन मॉडल में प्रत्येक अवलोकन के लिए कुक की दूरी की गणना करने के लिए COOKD कथन के साथ आउटपुट कथन का उपयोग कर सकते हैं:

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

अंतिम परिणाम तालिका प्रत्येक अवलोकन के लिए कुक दूरी के साथ मूल डेटासेट प्रदर्शित करती है:

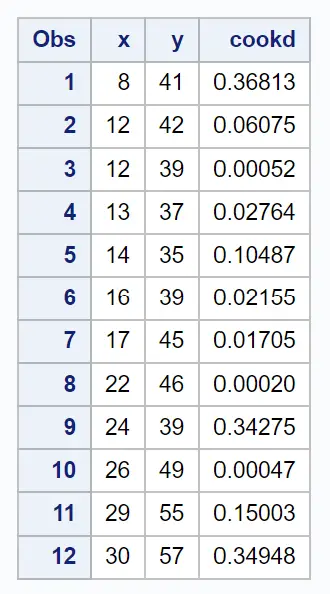
उदाहरण के लिए, हम देख सकते हैं:

• पहले अवलोकन के लिए कुक दूरी 0.36813 है।
• दूसरे अवलोकन के लिए कुक दूरी 0.06075 है।
• तीसरे अवलोकन के लिए कुक दूरी 0.00052 है।

और इसी तरह।

PROC REG प्रक्रिया आउटपुट में कई डायग्नोस्टिक प्लॉट भी तैयार करती है और कुक डिस्टेंस प्लॉट को इस आउटपुट में देखा जा सकता है:

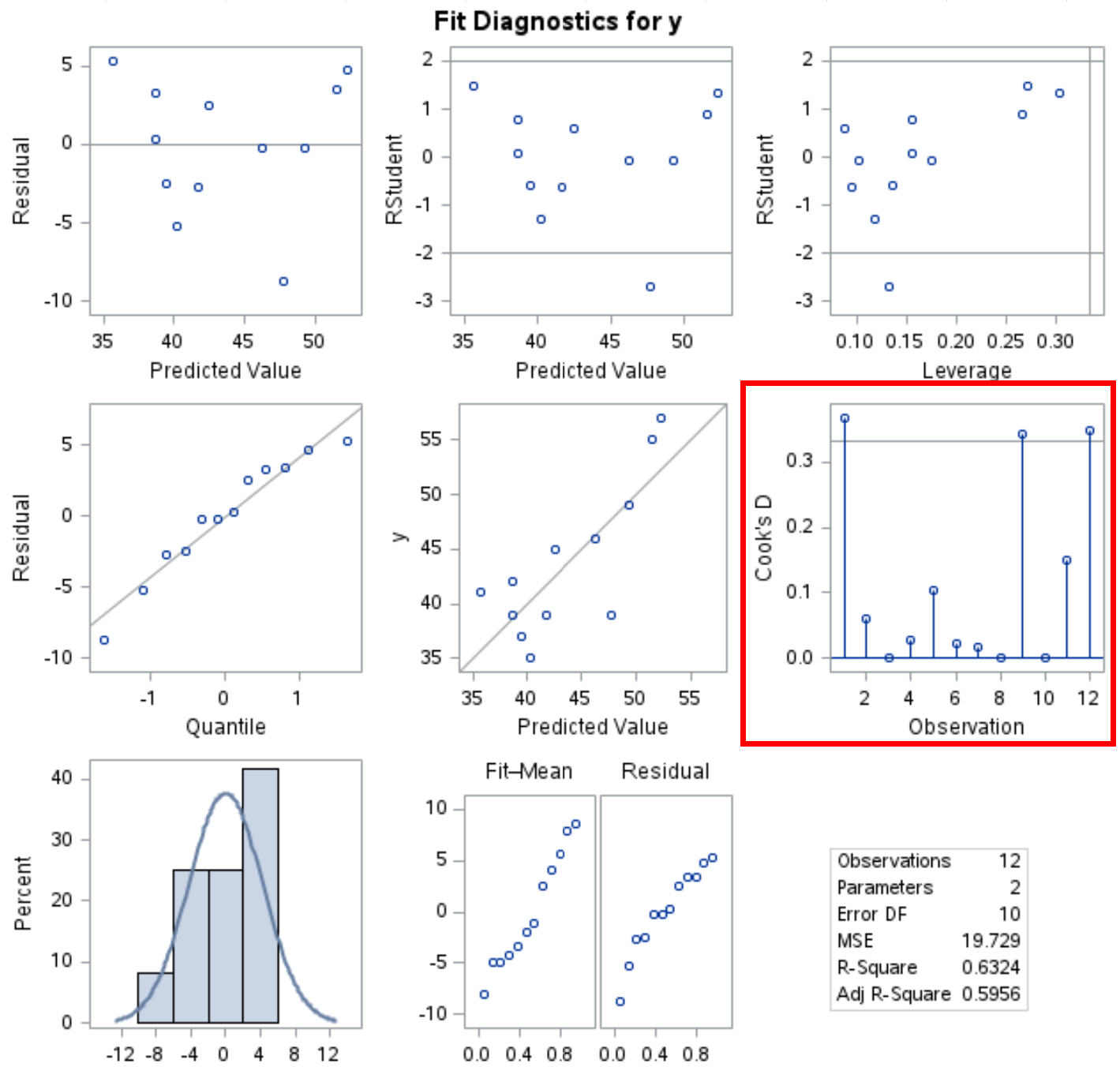
x-अक्ष अवलोकन संख्या दिखाता है और y-अक्ष प्रत्येक अवलोकन के लिए कुक दूरी दिखाता है।

ध्यान दें कि एक कटऑफ लाइन 4/n पर रखी गई है (इस मामले में n = 12, इसलिए कटऑफ 0.33 पर है) और हम देख सकते हैं कि डेटासेट में तीन अवलोकन इस लाइन से अधिक हैं।

यह इंगित करता है कि इन अवलोकनों का प्रतिगमन मॉडल पर बड़ा प्रभाव हो सकता है और मॉडल परिणामों की व्याख्या करने से पहले शायद अधिक बारीकी से जांच की जानी चाहिए।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य सामान्य कार्य कैसे करें:

एसएएस में एक अवशिष्ट प्लॉट कैसे बनाएं
एसएएस में हिस्टोग्राम कैसे बनाएं
एसएएस में पॉइंट क्लाउड कैसे बनाएं
एसएएस में आउटलेर्स की पहचान कैसे करें