एसएएस में मल्टीपल लीनियर रिग्रेशन कैसे करें

मल्टीपल लीनियर रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम दो या दो से अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को समझने के लिए कर सकते हैं।

यह ट्यूटोरियल बताता है कि एसएएस में मल्टीपल लीनियर रिग्रेशन कैसे करें।

चरण 1: डेटा बनाएं

मान लीजिए कि हम एक एकाधिक रेखीय प्रतिगमन मॉडल फिट करना चाहते हैं जो छात्रों के अंतिम परीक्षा ग्रेड की भविष्यवाणी करने के लिए अध्ययन में बिताए गए घंटों की संख्या और अभ्यास परीक्षाओं की संख्या का उपयोग करता है:

परीक्षा स्कोर = β ₀ + β ₁ (घंटे) + β ₂ (प्रारंभिक परीक्षा)

सबसे पहले, हम 20 छात्रों के लिए इस जानकारी वाला डेटासेट बनाने के लिए निम्नलिखित कोड का उपयोग करेंगे:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

चरण 2: एकाधिक रैखिक प्रतिगमन करें

इसके बाद, हम डेटा में एकाधिक रैखिक प्रतिगमन मॉडल को फिट करने के लिए proc reg का उपयोग करेंगे:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

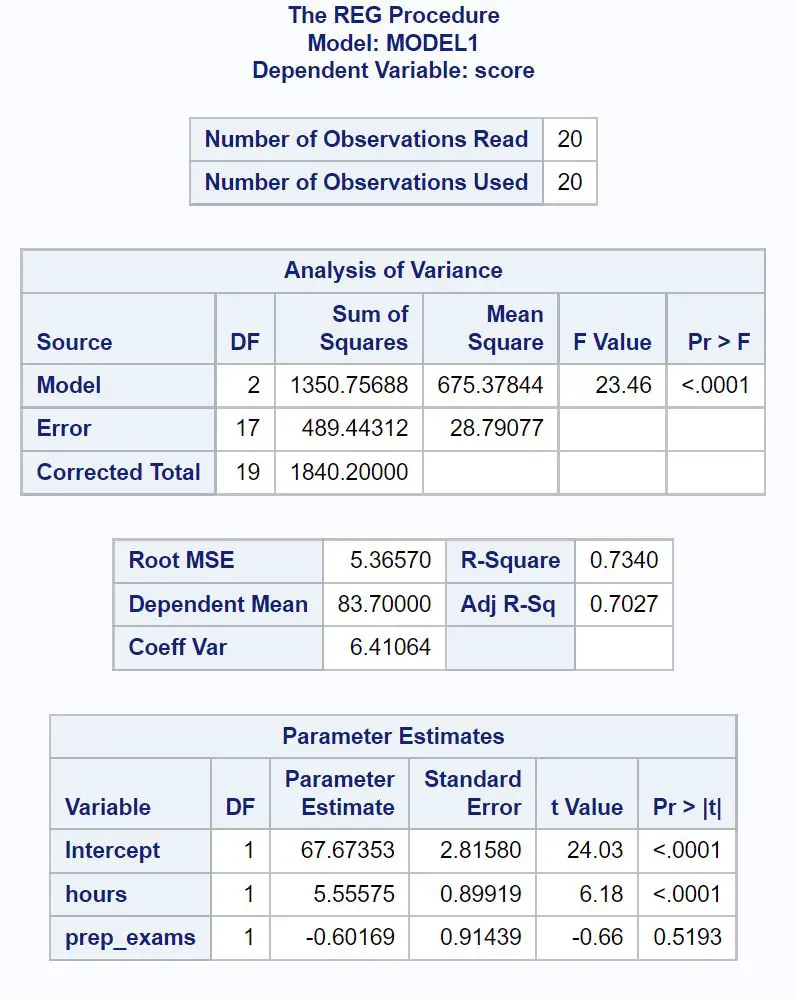
यहां प्रत्येक तालिका में सबसे प्रासंगिक संख्याओं की व्याख्या करने का तरीका बताया गया है:

गैप विश्लेषण तालिका:

प्रतिगमन मॉडल का समग्र एफ-मान 23.46 है और संबंधित पी-मान <0.0001 है।

चूँकि यह पी-मान 0.05 से कम है, हम यह निष्कर्ष निकालते हैं कि समग्र रूप से प्रतिगमन मॉडल सांख्यिकीय रूप से महत्वपूर्ण है।

मॉडल फ़िट तालिका:

आर-स्क्वायर मान हमें परीक्षा के अंकों में भिन्नता का प्रतिशत बताता है जिसे अध्ययन किए गए घंटों की संख्या और ली गई तैयारी परीक्षाओं की संख्या से समझाया जा सकता है।

सामान्य तौर पर, प्रतिगमन मॉडल का आर-वर्ग मान जितना बड़ा होगा, प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने में भविष्यवक्ता चर उतना ही बेहतर होगा।

इस मामले में, परीक्षा के अंकों में 73.4% भिन्नता को अध्ययन किए गए घंटों की संख्या और ली गई प्रारंभिक परीक्षाओं की संख्या से समझाया जा सकता है।

रूट एमएसई मान जानना भी उपयोगी है। यह प्रेक्षित मानों और प्रतिगमन रेखा के बीच की औसत दूरी को दर्शाता है।

इस प्रतिगमन मॉडल में, देखे गए मान प्रतिगमन रेखा से औसतन 5.3657 इकाइयों तक विचलित होते हैं।

पैरामीटर अनुमान की तालिका:

फिटेड रिग्रेशन समीकरण लिखने के लिए हम इस तालिका में पैरामीटर अनुमान मानों का उपयोग कर सकते हैं:

परीक्षा स्कोर = 67.674 + 5.556*(घंटे) – 0.602*(prep_exams)

हम अध्ययन के घंटों की संख्या और उनके द्वारा दी गई अभ्यास परीक्षाओं की संख्या के आधार पर, किसी छात्र के अनुमानित परीक्षा स्कोर को खोजने के लिए इस समीकरण का उपयोग कर सकते हैं।

उदाहरण के लिए, एक छात्र जो 3 घंटे पढ़ाई करता है और 2 प्रारंभिक परीक्षाएं देता है, उसे 83.1 का परीक्षा स्कोर प्राप्त करना चाहिए:

अनुमानित परीक्षा स्कोर = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

घंटों के लिए पी-मान (<0.0001) 0.05 से कम है, जिसका अर्थ है कि इसका परीक्षा परिणाम के साथ सांख्यिकीय रूप से महत्वपूर्ण संबंध है।

हालाँकि, प्रारंभिक परीक्षाओं के लिए पी-वैल्यू (0.5193) 0.05 से कम नहीं है, जिसका अर्थ है कि इसका परीक्षा परिणाम के साथ सांख्यिकीय रूप से महत्वपूर्ण संबंध नहीं है।

हम मॉडल से प्रारंभिक परीक्षाओं को हटाने का निर्णय ले सकते हैं, क्योंकि वे सांख्यिकीय रूप से महत्वपूर्ण नहीं हैं, और इसके बजाय एकमात्र भविष्यवक्ता चर के रूप में अध्ययन किए गए घंटों का उपयोग करके एक सरल रैखिक प्रतिगमन करते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य सामान्य कार्य कैसे करें:

एसएएस में सहसंबंध की गणना कैसे करें
एसएएस में सरल रैखिक प्रतिगमन कैसे करें
एसएएस में वन-वे एनोवा कैसे निष्पादित करें