वर्गों के योग के लिए एक सरल मार्गदर्शिका: एसएसटी, एसएसआर, एसएसई

रैखिक प्रतिगमन का उपयोग उस रेखा को खोजने के लिए किया जाता है जो डेटा के एक सेट को सबसे अच्छी तरह से “फिट” करती है।

हम अक्सर यह मापने के लिए वर्ग मानों के तीन अलग-अलग योगों का उपयोग करते हैं कि प्रतिगमन रेखा वास्तव में डेटा को कितनी अच्छी तरह फिट करती है:

1. कुल वर्गों का योग (एसएसटी) – व्यक्तिगत डेटा बिंदुओं (y _i ) और प्रतिक्रिया चर के माध्य ( y ) के बीच अंतर के वर्गों का योग।

• एसएसटी = Σ(y _i – y ) ²

2. वर्गों प्रतिगमन का योग (एसएसआर) – अनुमानित डेटा बिंदुओं (ŷ _i ) और प्रतिक्रिया चर के माध्य ( y ) के बीच अंतर के वर्गों का योग।

• एसएसआर = Σ(ŷ _i – y ) ²

3. वर्गों का योग त्रुटि (एसएसई) – अनुमानित डेटा बिंदुओं (ŷ _i ) और देखे गए डेटा बिंदुओं (y _i ) के बीच अंतर के वर्गों का योग।

• एसएसई = Σ(ŷ _i – y _i ) ²

इन तीन उपायों के बीच निम्नलिखित संबंध मौजूद है:

एसएसटी = एसएसआर + एसएसई

इसलिए यदि हम इनमें से दो माप जानते हैं, तो हम तीसरे की गणना करने के लिए सरल बीजगणित का उपयोग कर सकते हैं।

एसएसआर, एसएसटी और आर-स्क्वायर

आर-वर्ग , जिसे कभी-कभी निर्धारण का गुणांक भी कहा जाता है, एक माप है कि एक रैखिक प्रतिगमन मॉडल डेटा सेट में कितनी अच्छी तरह फिट बैठता है। यह प्रतिक्रिया चर में भिन्नता के अनुपात का प्रतिनिधित्व करता है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है।

आर-वर्ग मान 0 से 1 तक हो सकता है। 0 का मान इंगित करता है कि प्रतिक्रिया चर को भविष्यवक्ता चर द्वारा बिल्कुल भी समझाया नहीं जा सकता है। 1 का मान इंगित करता है कि प्रतिक्रिया चर को भविष्यवक्ता चर द्वारा त्रुटि के बिना पूरी तरह से समझाया जा सकता है।

एसएसआर और एसएसटी का उपयोग करके, हम आर वर्ग की गणना निम्नानुसार कर सकते हैं:

आर वर्ग = एसएसआर/एसएसटी

उदाहरण के लिए, यदि किसी दिए गए प्रतिगमन मॉडल के लिए एसएसआर 137.5 है और एसएसटी 156 है, तो हम आर वर्ग की गणना निम्नानुसार करेंगे:

आर वर्ग = 137.5 / 156 = 0.8814

यह हमें बताता है कि प्रतिक्रिया चर में 88.14% भिन्नता को भविष्यवक्ता चर द्वारा समझाया जा सकता है।

एसएसटी, एसएसआर, एसएसई की गणना करें: चरण दर चरण उदाहरण

मान लीजिए कि हमारे पास निम्नलिखित डेटासेट हैं जो छह अलग-अलग छात्रों द्वारा उनके अंतिम परीक्षा अंकों के साथ अध्ययन किए गए घंटों की संख्या दर्शाते हैं:

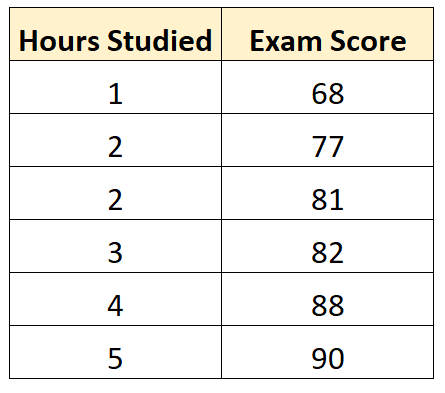
कुछ सांख्यिकीय सॉफ़्टवेयर (जैसे आर , एक्सेल , पायथन ) या यहां तक कि हाथ से भी, हम देख सकते हैं कि सबसे उपयुक्त लाइन है:

स्कोर = 66.615 + 5.0769*(घंटे)

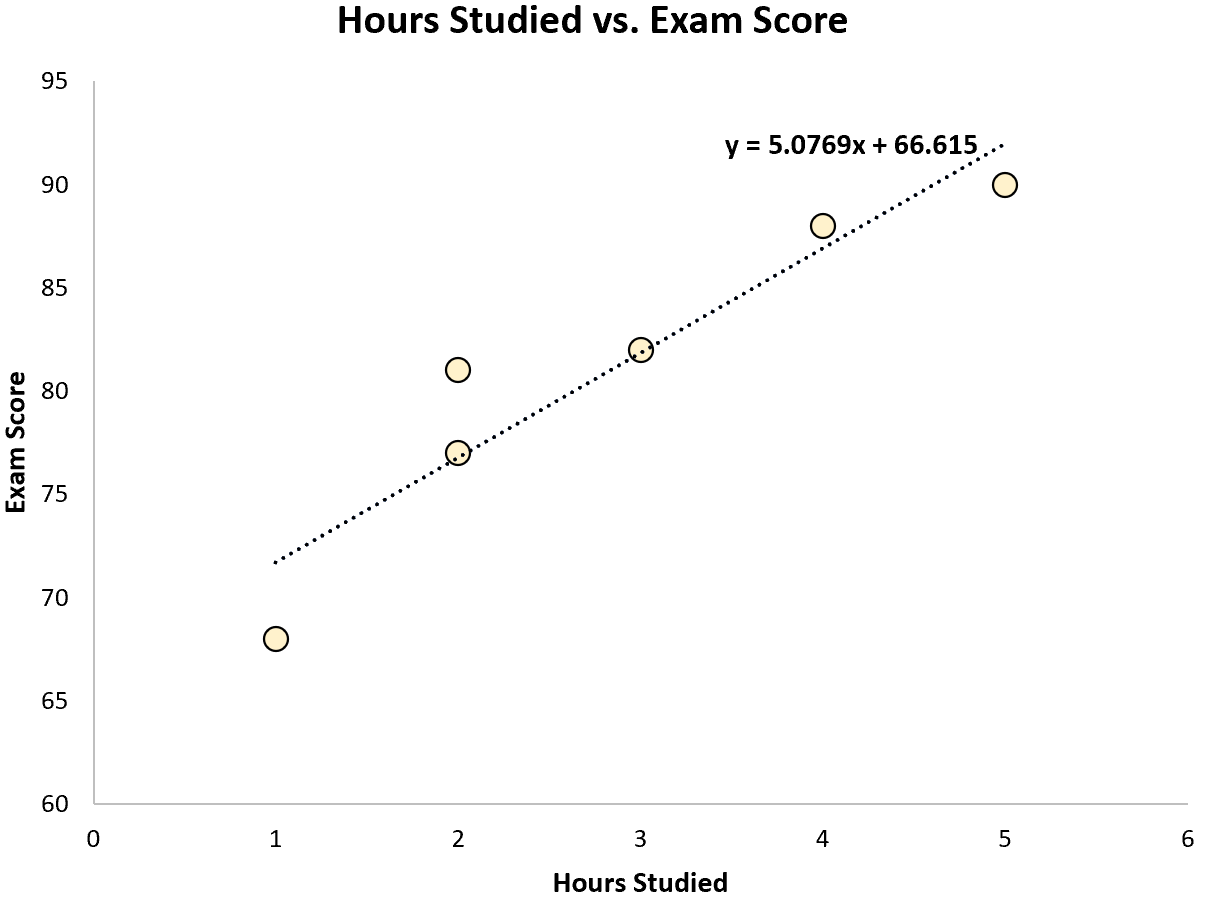
एक बार जब हम सबसे उपयुक्त समीकरण की रेखा जान लेते हैं, तो हम एसएसटी, एसएसआर और एसएसई की गणना करने के लिए निम्नलिखित चरणों का उपयोग कर सकते हैं:

चरण 1: प्रतिक्रिया चर के माध्य की गणना करें।

प्रतिक्रिया चर ( y ) का माध्य 81 निकला।

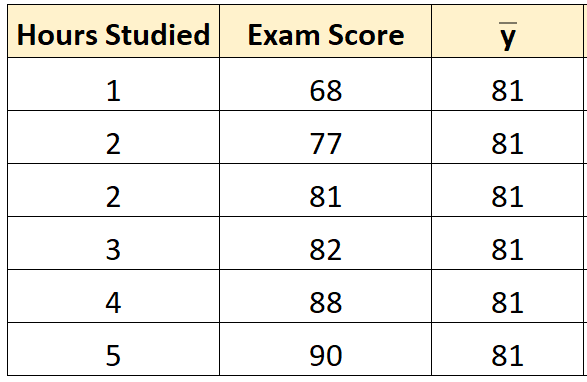
चरण 2: प्रत्येक अवलोकन के लिए अनुमानित मूल्य की गणना करें।

फिर हम प्रत्येक छात्र के लिए अनुमानित परीक्षा स्कोर () की गणना करने के लिए सर्वोत्तम-फिट समीकरण की पंक्ति का उपयोग कर सकते हैं।

उदाहरण के लिए, एक घंटा अध्ययन करने वाले छात्र के लिए अनुमानित परीक्षा ग्रेड है:

स्कोर = 66.615 + 5.0769*(1) = 71.69 ।

हम प्रत्येक छात्र के लिए अनुमानित अंक ज्ञात करने के लिए समान दृष्टिकोण का उपयोग कर सकते हैं:

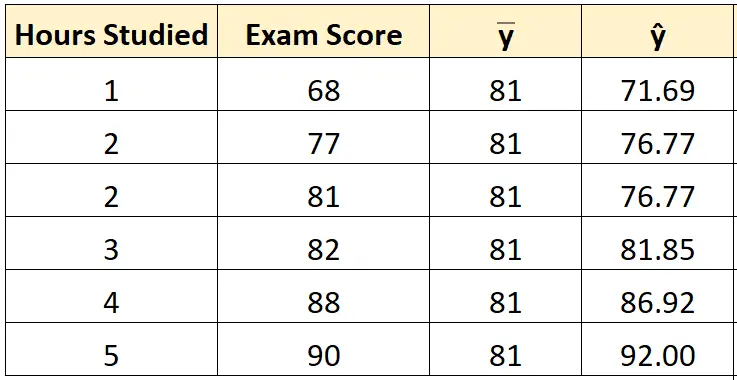
चरण 3: वर्गों के कुल योग (एसएसटी) की गणना करें।

तब हम कुल वर्गों के योग की गणना कर सकते हैं।

उदाहरण के लिए, पहले छात्र के लिए वर्गों का कुल योग है:

(y _i – y ) ² = (68 – 81) ² = 169 .

हम प्रत्येक छात्र के लिए वर्गों का कुल योग ज्ञात करने के लिए समान दृष्टिकोण का उपयोग कर सकते हैं:

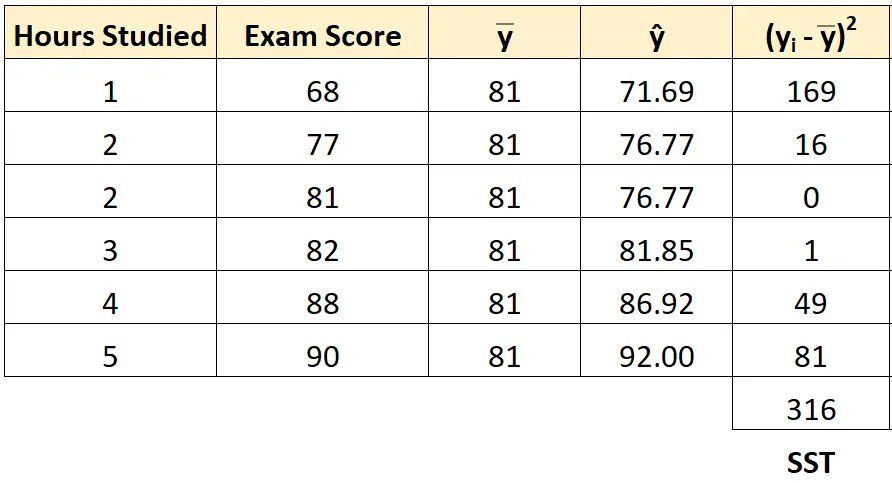
वर्गों का कुल योग 316 होता है।

चरण 4: वर्ग प्रतिगमन (एसएसआर) के योग की गणना करें।

फिर हम वर्गों के प्रतिगमन के योग की गणना कर सकते हैं।

उदाहरण के लिए, पहले छात्र के लिए वर्ग प्रतिगमन का योग है:

( _ŷi – y ) ² = (71.69 – 81) ² = 86.64 ।

हम प्रत्येक छात्र के लिए वर्गों के योग का प्रतिगमन ज्ञात करने के लिए समान दृष्टिकोण का उपयोग कर सकते हैं:

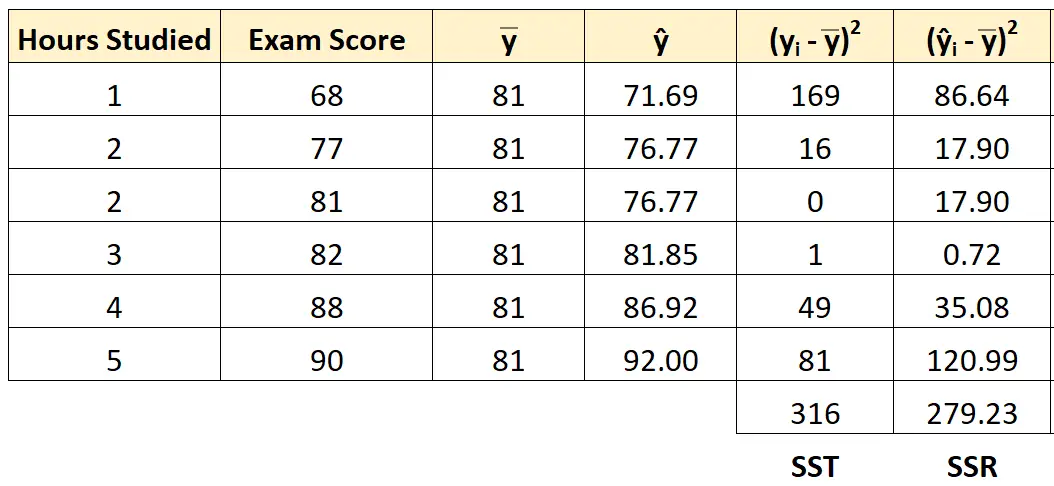
वर्ग प्रतिगमन का योग 279.23 हो जाता है।

चरण 5: वर्ग त्रुटि (एसएसई) के योग की गणना करें।

तब हम वर्गों के योग की त्रुटि की गणना कर सकते हैं।

उदाहरण के लिए, पहले छात्र के लिए वर्ग त्रुटि का योग है:

(ŷ _i – y _i ) ² = (71.69 – 68) ² = 13.63 .

हम प्रत्येक छात्र के लिए वर्गों की त्रुटि का योग ज्ञात करने के लिए समान दृष्टिकोण का उपयोग कर सकते हैं:

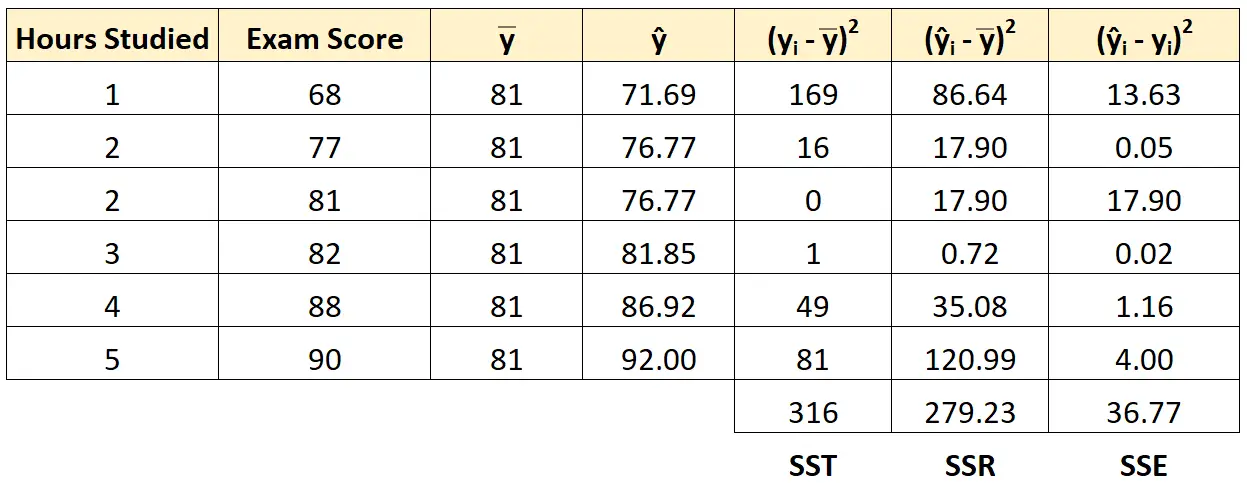
हम सत्यापित कर सकते हैं कि SST = SSR + SSE

• एसएसटी = एसएसआर + एसएसई
• 316 = 279.23 + 36.77

हम निम्नलिखित समीकरण का उपयोग करके प्रतिगमन मॉडल के आर वर्ग की गणना भी कर सकते हैं:

• आर वर्ग = एसएसआर/एसएसटी
• आर वर्ग = 279.23/316
• आर वर्ग = 0.8836

यह हमें बताता है कि परीक्षा के अंकों में 88.36% भिन्नता को अध्ययन किए गए घंटों की संख्या से समझाया जा सकता है।

अतिरिक्त संसाधन

आप किसी भी सरल रैखिक प्रतिगमन रेखा के लिए स्वचालित रूप से एसएसटी, एसएसआर और एसएसई की गणना करने के लिए निम्नलिखित कैलकुलेटर का उपयोग कर सकते हैं:

एसएसटी कैलकुलेटर
आरएसएस कैलकुलेटर
ईएसएस कैलकुलेटर