Spss में roc कर्व कैसे बनाएं और व्याख्या करें

लॉजिस्टिक रिग्रेशन एक सांख्यिकीय पद्धति है जिसका उपयोग हम रिग्रेशन मॉडल को फिट करने के लिए करते हैं जब प्रतिक्रिया चर द्विआधारी होता है। यह मूल्यांकन करने के लिए कि लॉजिस्टिक रिग्रेशन मॉडल डेटा सेट में कितनी अच्छी तरह फिट बैठता है, हम निम्नलिखित दो मैट्रिक्स देख सकते हैं:

• संवेदनशीलता: संभावना है कि मॉडल किसी अवलोकन के लिए सकारात्मक परिणाम की भविष्यवाणी करता है जब परिणाम वास्तव में सकारात्मक होता है।
• विशिष्टता: संभावना है कि मॉडल किसी अवलोकन के लिए नकारात्मक परिणाम की भविष्यवाणी करता है जब परिणाम वास्तव में नकारात्मक होता है।

इन दो मेट्रिक्स की कल्पना करने का एक सरल तरीका एक आरओसी वक्र बनाना है, जो एक ग्राफ है जो लॉजिस्टिक रिग्रेशन मॉडल की संवेदनशीलता और विशिष्टता को प्रदर्शित करता है।

यह ट्यूटोरियल बताता है कि SPSS में ROC वक्र कैसे बनाएं और उसकी व्याख्या कैसे करें।

उदाहरण: SPSS में ROC वक्र

मान लें कि हमारे पास निम्नलिखित डेटा सेट है जो दिखाता है कि बास्केटबॉल खिलाड़ी को एनबीए में शामिल किया गया था या नहीं (0 = नहीं, 1 = हां) और साथ ही कॉलेज में उसके प्रति गेम औसत अंक:

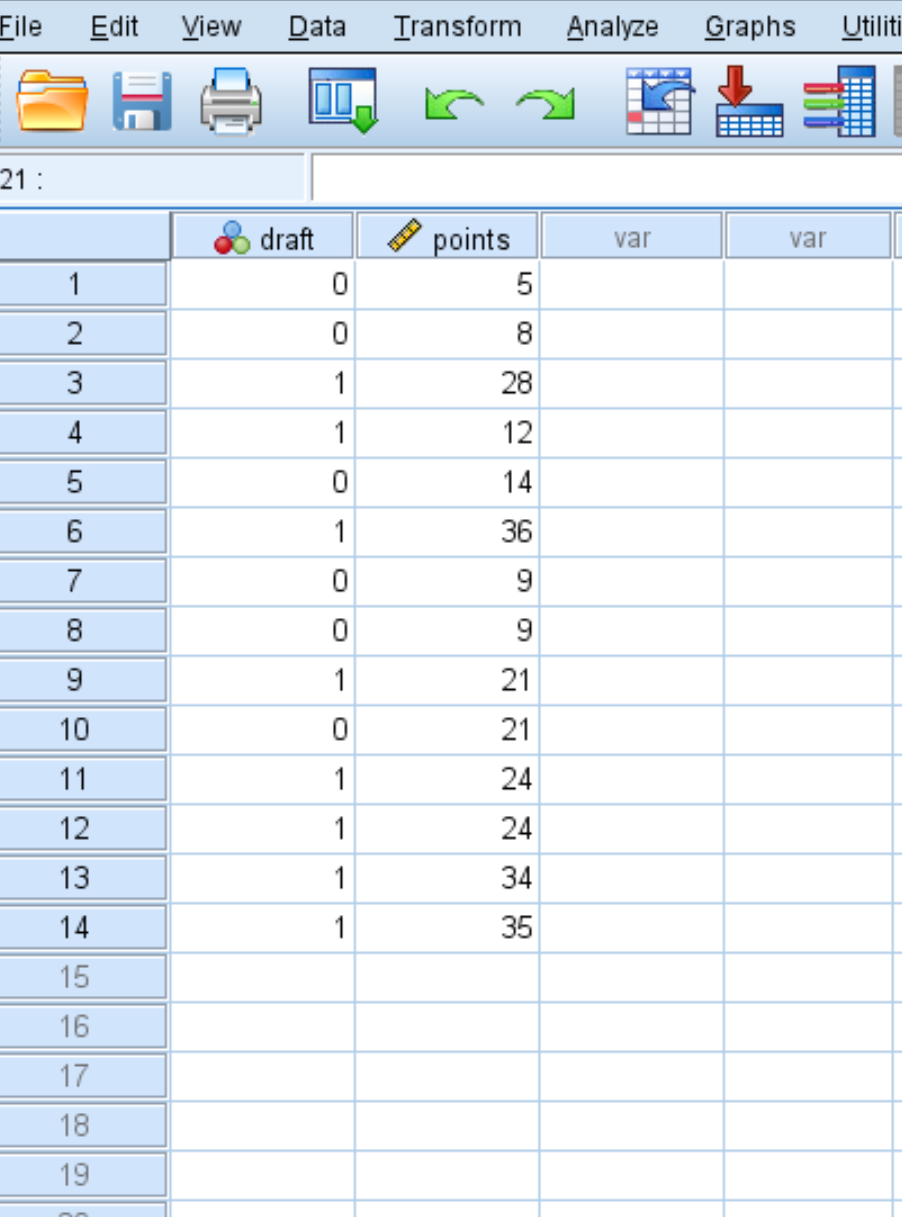
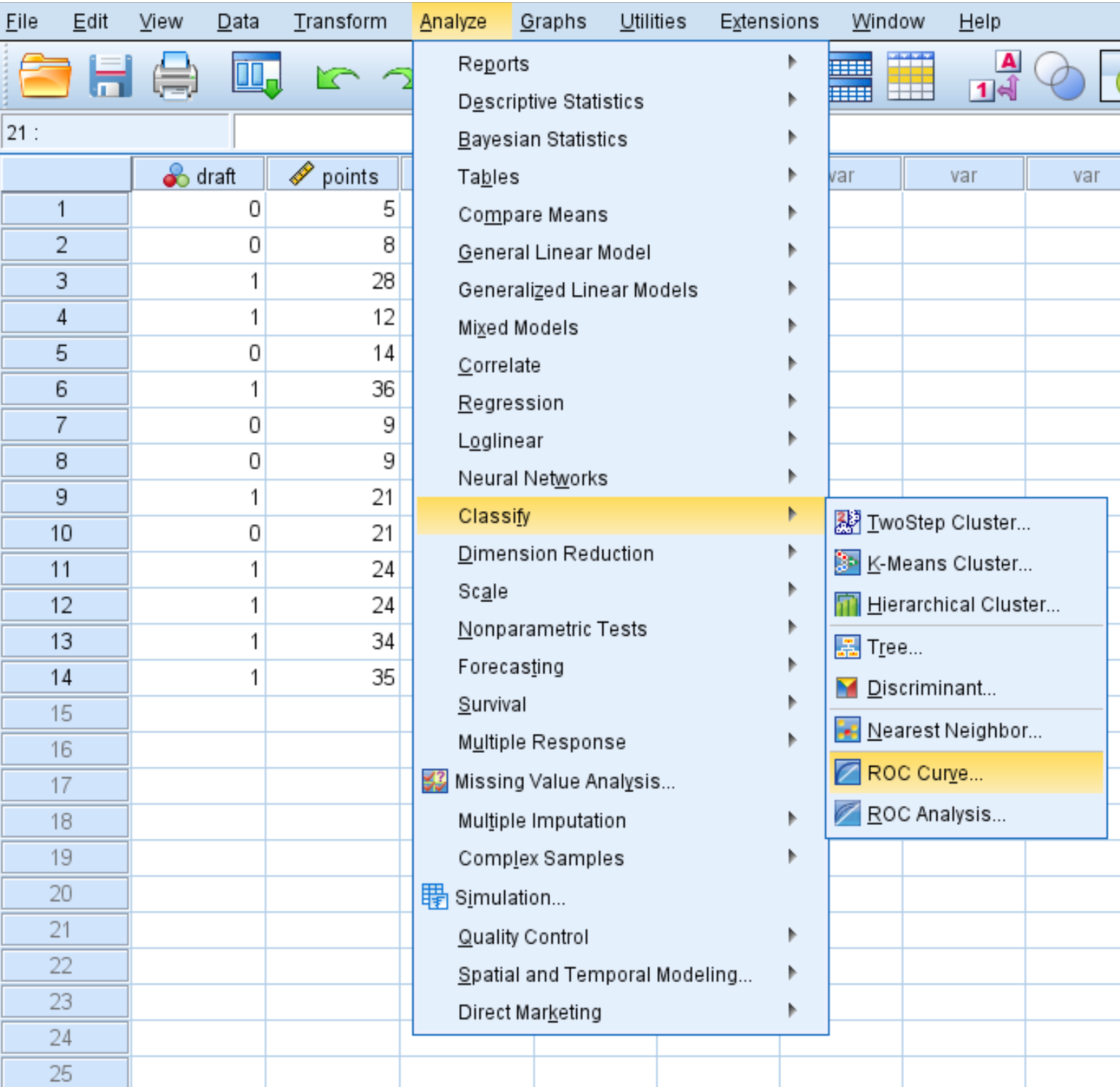
इस डेटासेट के लिए ROC वक्र बनाने के लिए, विश्लेषण टैब पर क्लिक करें, फिर वर्गीकृत करें , फिर ROC वक्र पर क्लिक करें:

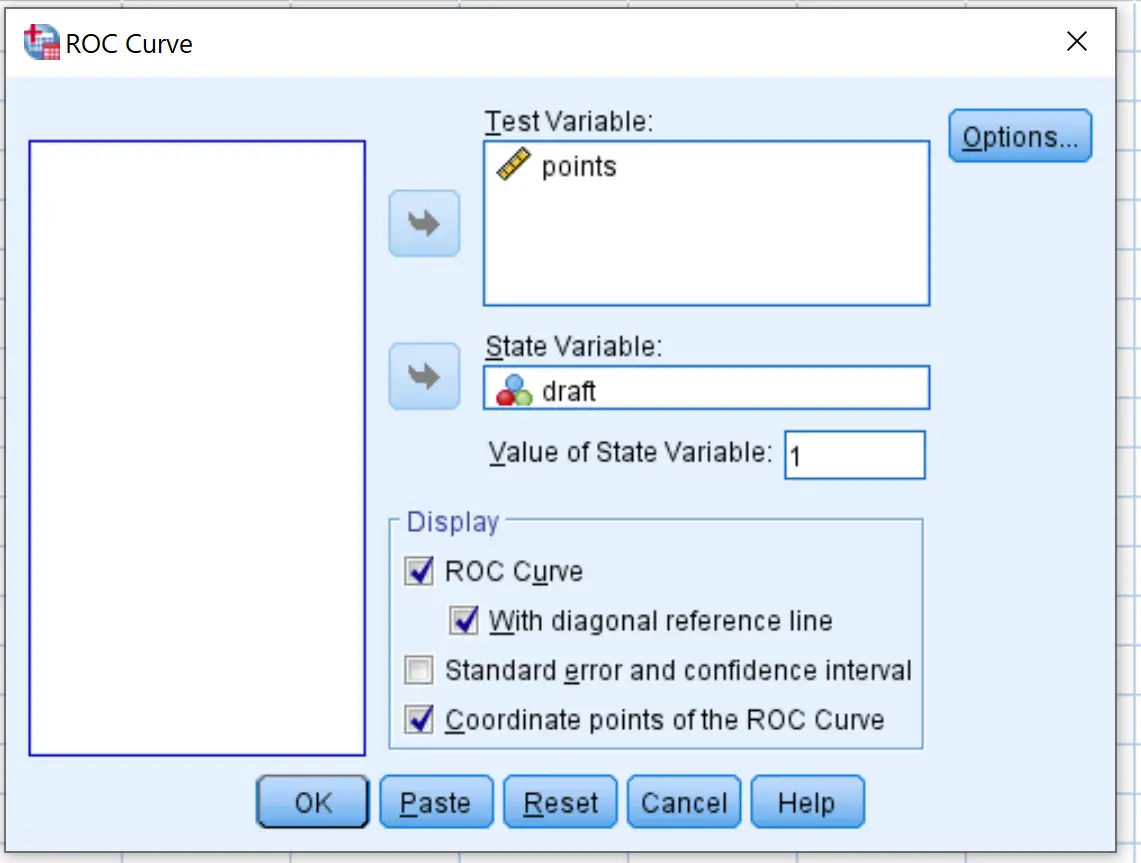
दिखाई देने वाली नई विंडो में, ड्राफ्ट वेरिएबल को स्टेट वेरिएबल लेबल वाले क्षेत्र में खींचें। राज्य चर का मान 1 पर सेट करें। (यह वह मान है जो इंगित करता है कि एक खिलाड़ी को ड्राफ्ट किया गया है)। वेरिएबल बिंदुओं को टेस्ट वेरिएबल लेबल वाले क्षेत्र में खींचें।

विकर्ण संदर्भ रेखा और आरओसी वक्र बिंदु निर्देशांक के बगल में स्थित बक्सों को चेक करें। फिर ओके पर क्लिक करें.

यहां परिणाम की व्याख्या करने का तरीका बताया गया है:

फ़ाइल प्रसंस्करण का सारांश:

यह तालिका डेटासेट में सकारात्मक और नकारात्मक मामलों की कुल संख्या प्रदर्शित करती है। इस उदाहरण में, 8 खिलाड़ियों को ड्राफ्ट किया गया (सकारात्मक परिणाम) और 6 खिलाड़ियों को ड्राफ्ट नहीं किया गया (नकारात्मक परिणाम):

आरओसी वक्र:

रिसीवर ऑपरेटिंग कैरेक्टरिस्टिक (आरओसी) वक्र संवेदनशीलता मान बनाम विशिष्टता 1 का एक प्लॉट है क्योंकि थ्रेशोल्ड मान 0 से 1 में बदलता है:

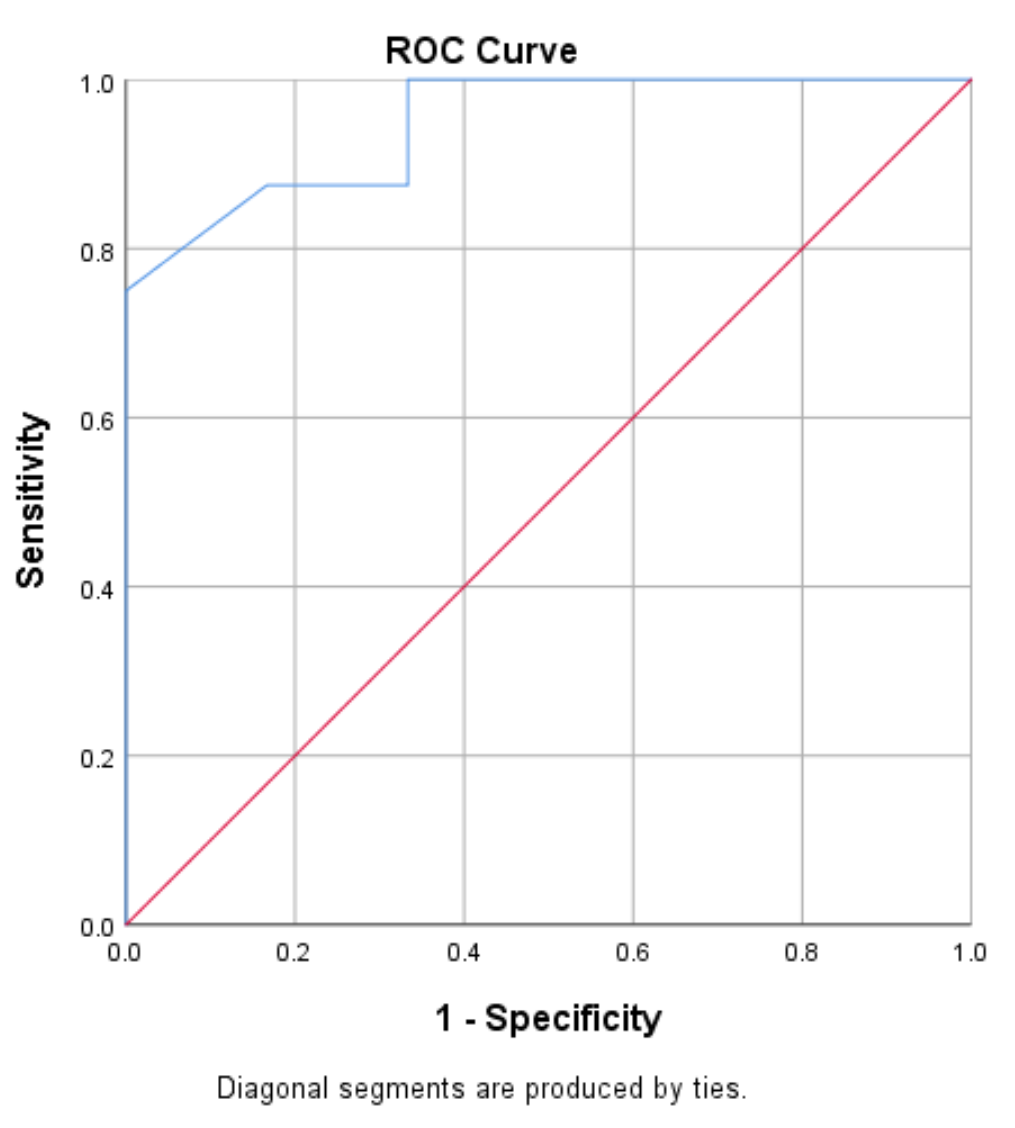
उच्च संवेदनशीलता और विशिष्टता वाले मॉडल में एक आरओसी वक्र होगा जो प्लॉट के ऊपरी बाएं कोने में फिट बैठता है। कम संवेदनशीलता और कम विशिष्टता वाले मॉडल में 45 डिग्री विकर्ण के करीब एक वक्र होगा।

हम देख सकते हैं कि इस उदाहरण में आरओसी वक्र (नीली रेखा) प्लॉट के ऊपरी बाएँ कोने को छूती है, यह दर्शाता है कि मॉडल खिलाड़ियों के प्रति गेम औसत अंकों के आधार पर यह अनुमान लगाने का अच्छा काम कर रहा है कि उन्हें ड्राफ्ट किया जाएगा या नहीं। . .

वक्र के नीचे का क्षेत्र:

वक्र के नीचे का क्षेत्र हमें सकारात्मक और नकारात्मक परिणामों के बीच अंतर करने की मॉडल की क्षमता का अंदाजा देता है। AUC 0 से 1 तक हो सकता है। AUC जितना अधिक होगा, मॉडल परिणामों को सही ढंग से वर्गीकृत करने में उतना ही बेहतर होगा।

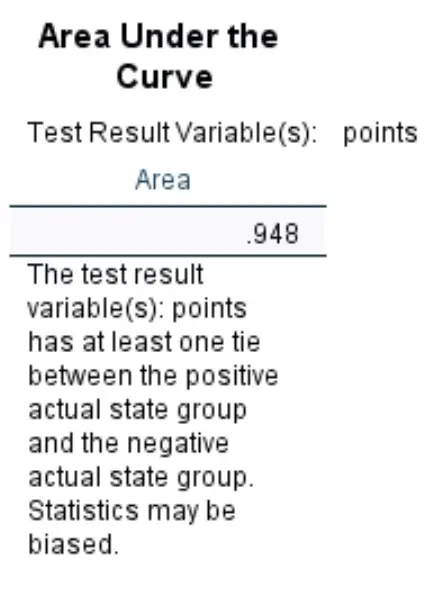
हम देख सकते हैं कि इस विशेष लॉजिस्टिक रिग्रेशन मॉडल के लिए AUC 0.948 है, जो बहुत अधिक है। यह इंगित करता है कि मॉडल यह भविष्यवाणी करने का अच्छा काम करता है कि किसी खिलाड़ी को ड्राफ्ट किया जाएगा या नहीं।

वक्र के निर्देशांक:

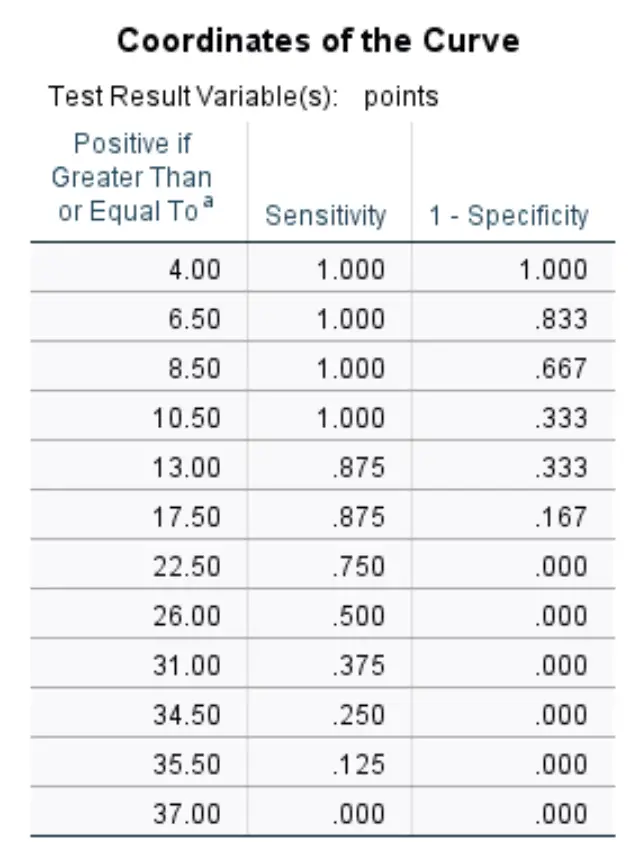
यह अंतिम तालिका विभिन्न सीमाओं के लिए आरओसी वक्र की संवेदनशीलता और विशिष्टता 1 प्रदर्शित करती है।

उदाहरण के लिए:

यदि हम सीमा 8.50 की अनुमति देते हैं, तो इसका मतलब है कि हम उम्मीद करते हैं कि प्रति गेम 8.50 से कम अंक प्राप्त करने वाले किसी भी खिलाड़ी को ड्राफ्ट नहीं किया जाएगा, और जो भी खिलाड़ी प्रति गेम 8.50 से अधिक अंक प्राप्त करता है उसे ड्राफ्ट किया जाएगा।

इसे एक सीमा के रूप में उपयोग करते हुए, हमारी संवेदनशीलता 100% होगी (क्योंकि प्रति गेम 8.50 से कम अंक हासिल करने वाले प्रत्येक खिलाड़ी को वास्तव में ड्राफ्ट नहीं किया गया था) और हमारी विशिष्टता 1 66.7% होगी (क्योंकि 12 में से 8 खिलाड़ी जिन्होंने 8.50 से अधिक अंक बनाए थे) प्रति गेम ड्राफ्ट किया गया था)।

उपरोक्त तालिका हमें प्रत्येक संभावित सीमा के लिए संवेदनशीलता और विशिष्टता 1 देखने की अनुमति देती है।