एसपीएसएस में सहसंबंध मैट्रिक्स कैसे बनाएं

सहसंबंध मैट्रिक्स एक वर्गाकार तालिका है जो डेटा सेट में विभिन्न चर के बीच पियर्सन सहसंबंध गुणांक दिखाती है।

एक अनुस्मारक के रूप में, पियर्सन सहसंबंध गुणांक दो चर के बीच रैखिक संबंध का एक माप है । यह -1 और 1 के बीच का मान लेता है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

सहसंबंध गुणांक शून्य से जितना अधिक होगा, दोनों चरों के बीच संबंध उतना ही मजबूत होगा।

यह ट्यूटोरियल बताता है कि एसपीएसएस में सहसंबंध मैट्रिक्स कैसे बनाएं और व्याख्या करें।

उदाहरण: एसपीएसएस में सहसंबंध मैट्रिक्स कैसे बनाएं

इस डेटासेट के लिए सहसंबंध मैट्रिक्स बनाने के लिए निम्नलिखित चरणों का पालन करें जो आठ बास्केटबॉल खिलाड़ियों की औसत सहायता, रिबाउंड और अंक प्रदर्शित करता है:

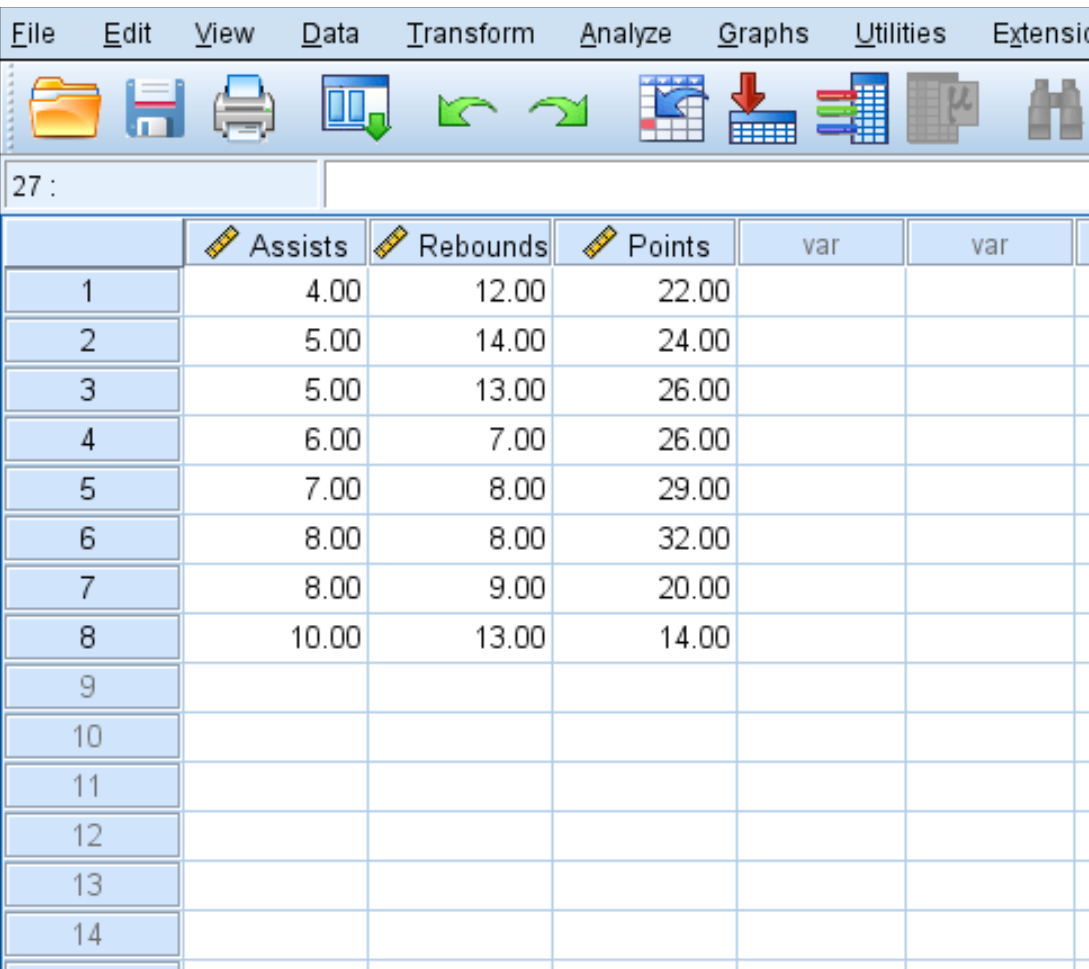
चरण 1: द्विचर सहसंबंध का चयन करें।

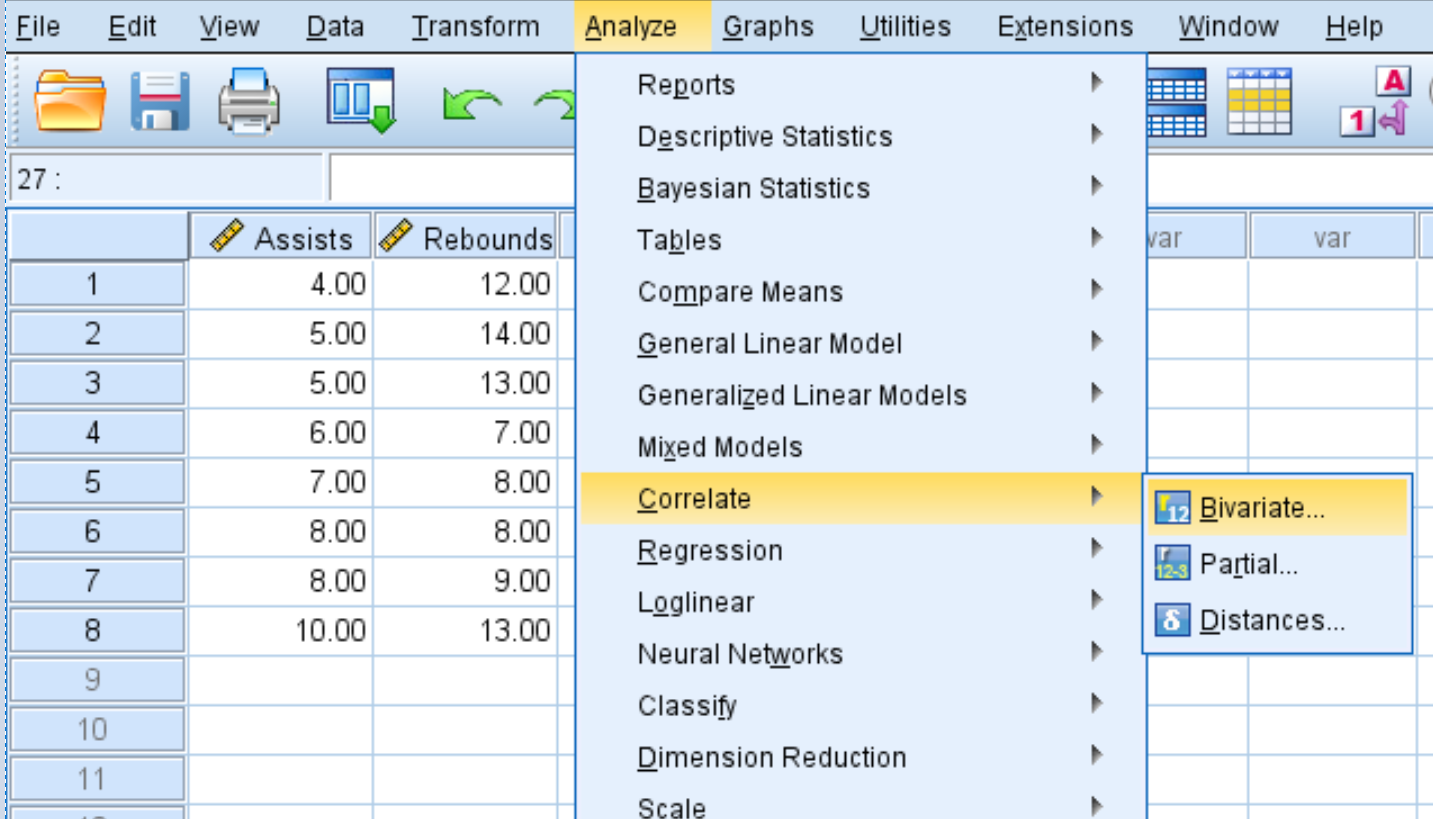
• विश्लेषण टैब पर क्लिक करें.
• सहसंबंधित करें पर क्लिक करें.
• Bivariate पर क्लिक करें.

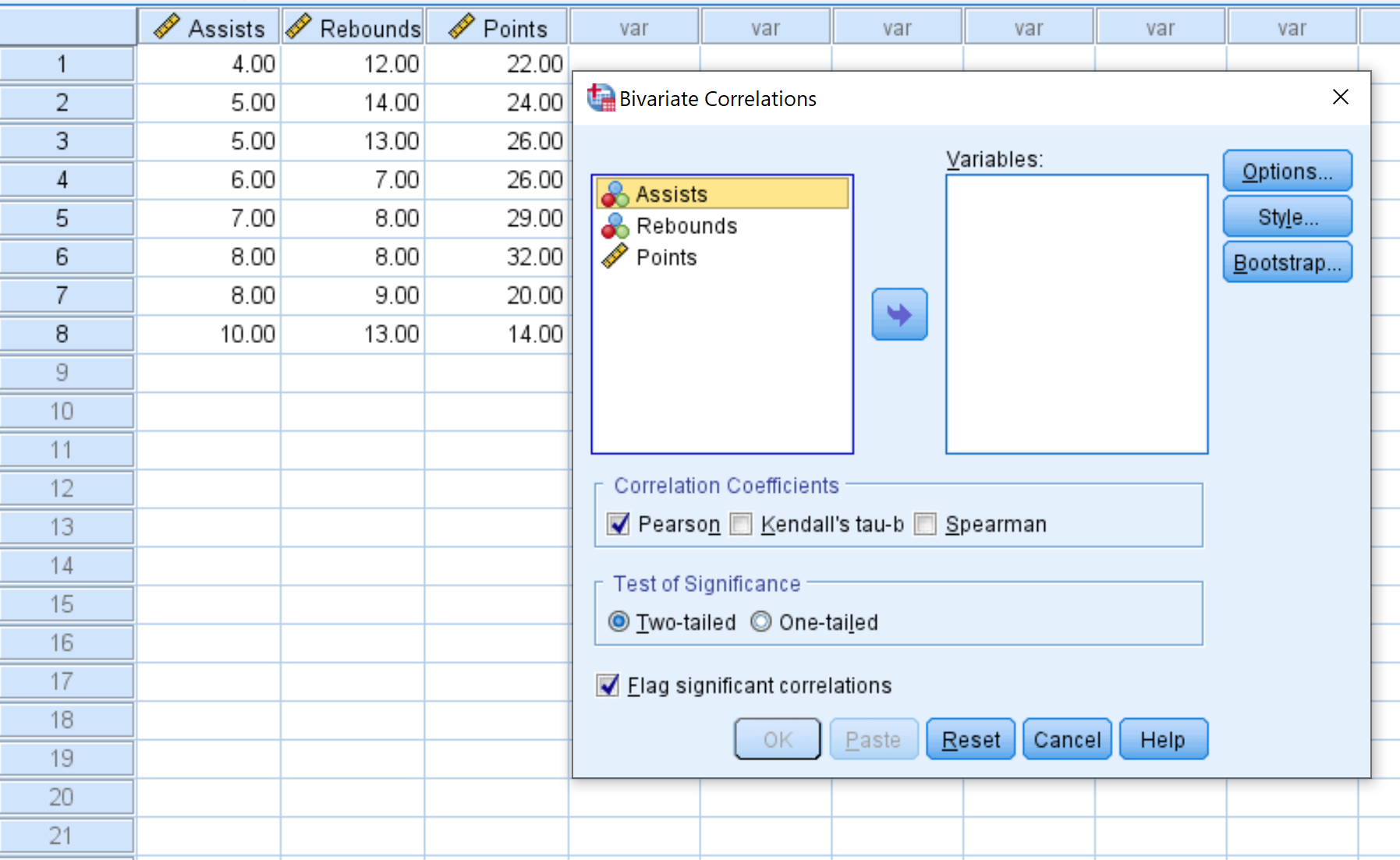
चरण 2: सहसंबंध मैट्रिक्स बनाएं।

डेटासेट में प्रत्येक वेरिएबल प्रारंभ में बाएं बॉक्स में प्रदर्शित किया जाएगा:

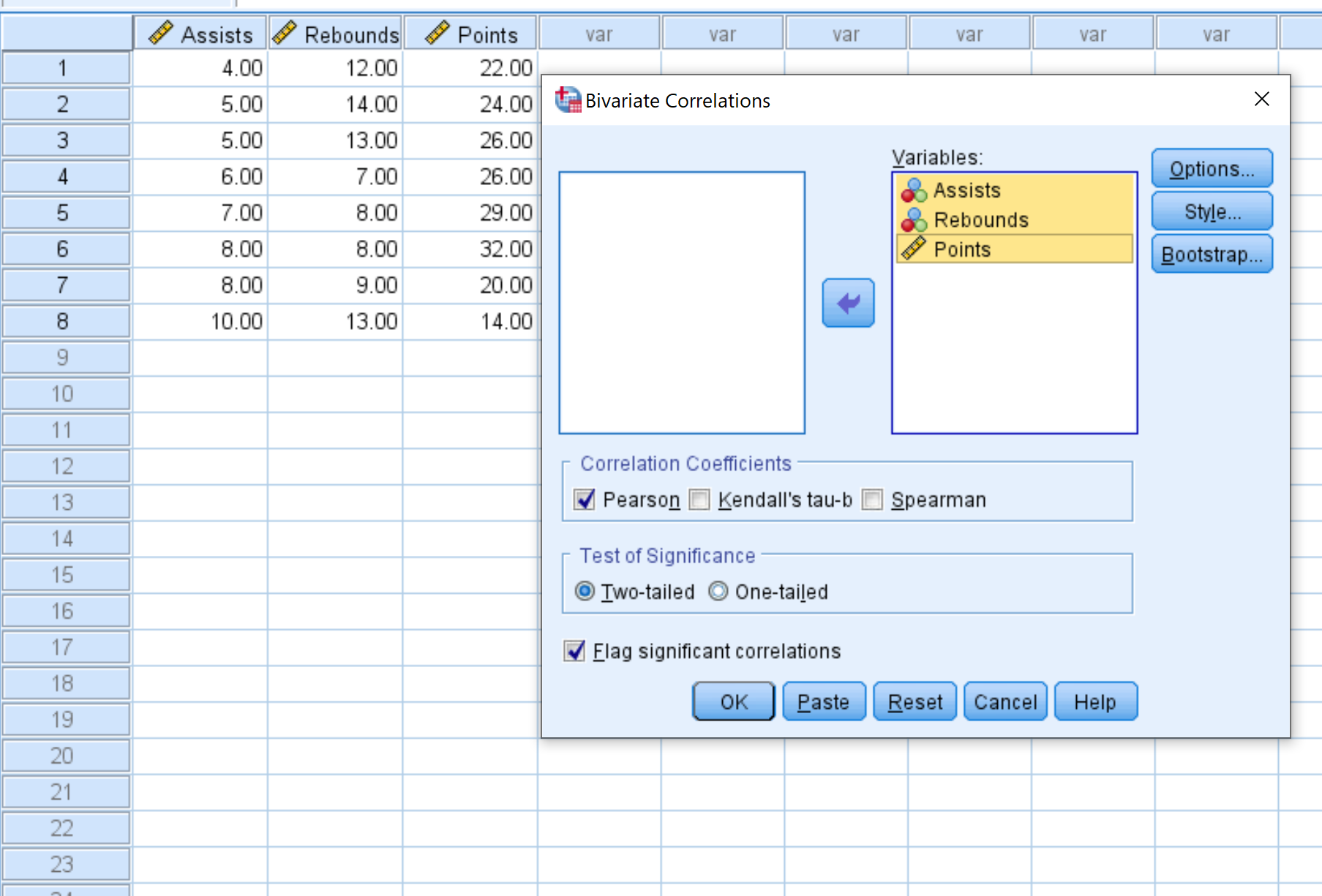
• प्रत्येक वेरिएबल का चयन करें जिसे आप सहसंबंध मैट्रिक्स में शामिल करना चाहते हैं और उन्हें वेरिएबल बॉक्स में स्थानांतरित करने के लिए तीर पर क्लिक करें। इस उदाहरण में हम तीनों वेरिएबल्स का उपयोग करेंगे।
• सहसंबंध गुणांक के अंतर्गत, चुनें कि क्या आप पियर्सन के सहसंबंध, केंडल के ताऊ, या स्पीयरमैन के सहसंबंध का उपयोग करना चाहते हैं। इस उदाहरण के लिए हम इसे पियर्सन के रूप में छोड़ देंगे।
• महत्व परीक्षण के अंतर्गत, चुनें कि क्या आप यह निर्धारित करने के लिए दो-पुच्छीय या एक-पुच्छीय परीक्षण का उपयोग करना चाहते हैं कि दो चरों का सांख्यिकीय रूप से महत्वपूर्ण संबंध है या नहीं। हम इसे दो-पूंछ के रूप में छोड़ देंगे।
• यदि आप चाहते हैं कि एसपीएसएस उन चरों की रिपोर्ट करे जो महत्वपूर्ण रूप से सहसंबद्ध हैं तो महत्वपूर्ण सहसंबंधों की रिपोर्ट करें के बगल में स्थित बॉक्स को चेक करें।
• अंत में, OK पर क्लिक करें।

एक बार जब आप ओके पर क्लिक करते हैं, तो निम्नलिखित सहसंबंध मैट्रिक्स प्रकट होता है:

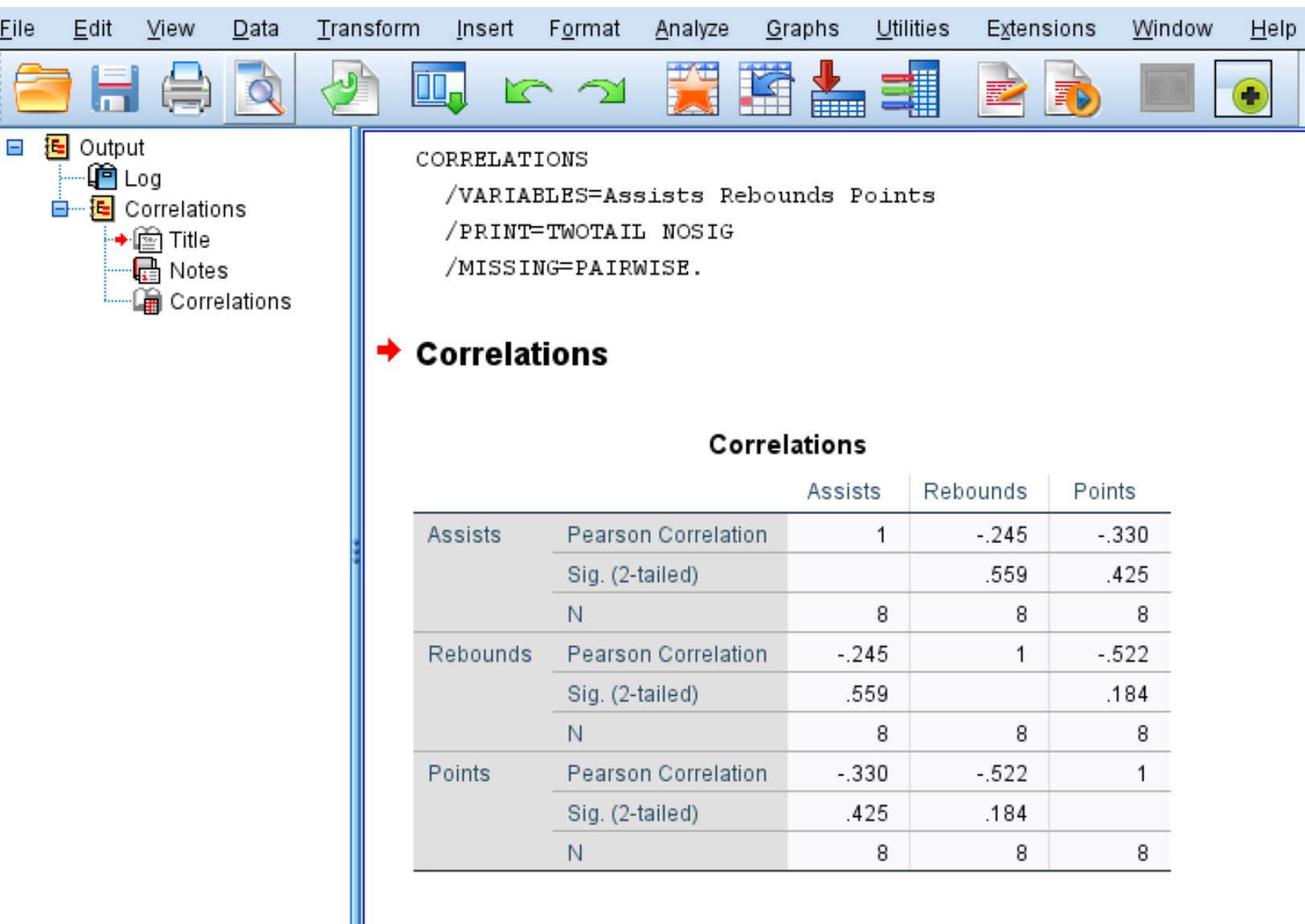
चरण 3: सहसंबंध मैट्रिक्स की व्याख्या करें।

सहसंबंध मैट्रिक्स प्रत्येक चर के लिए निम्नलिखित तीन माप प्रदर्शित करता है:

• पियर्सन सहसंबंध: -1 से 1 तक के दो चरों के बीच रैखिक संबंध का माप।
• सिग. (दो-पूंछ): सहसंबंध गुणांक से जुड़ा दो-पूंछ वाला पी-मान। यह आपको बताता है कि क्या दो चरों में सांख्यिकीय रूप से महत्वपूर्ण संबंध है (उदाहरण के लिए यदि पी <0.05)
• एन: पियर्सन सहसंबंध गुणांक की गणना के लिए उपयोग किए जाने वाले जोड़े की संख्या।

उदाहरण के लिए, यहां असिस्ट वेरिएबल के परिणाम की व्याख्या करने का तरीका बताया गया है:

• सहायता और रिबाउंड के बीच पियर्सन सहसंबंध गुणांक -0.245 है। चूँकि यह संख्या ऋणात्मक है, इसका अर्थ है कि इन दोनों चरों का ऋणात्मक संबंध है।
• सहायता और रिबाउंड के लिए पियर्सन सहसंबंध गुणांक से जुड़ा पी-मान 0.559 है। चूँकि यह मान 0.05 से कम नहीं है, इसलिए दोनों चरों का सांख्यिकीय रूप से महत्वपूर्ण संबंध नहीं है।
• पियर्सन सहसंबंध गुणांक की गणना करने के लिए उपयोग की जाने वाली जोड़ियों की संख्या 8 थी (उदाहरण के लिए, इस गणना में खिलाड़ियों के 8 जोड़े का उपयोग किया गया था)।

चरण 4: सहसंबंध मैट्रिक्स की कल्पना करें।

आप प्रत्येक चर के बीच रैखिक संबंध को देखने के लिए एक स्कैटर प्लॉट मैट्रिक्स भी बना सकते हैं।

• चार्ट टैब पर क्लिक करें.
• चार्ट बिल्डर पर क्लिक करें.

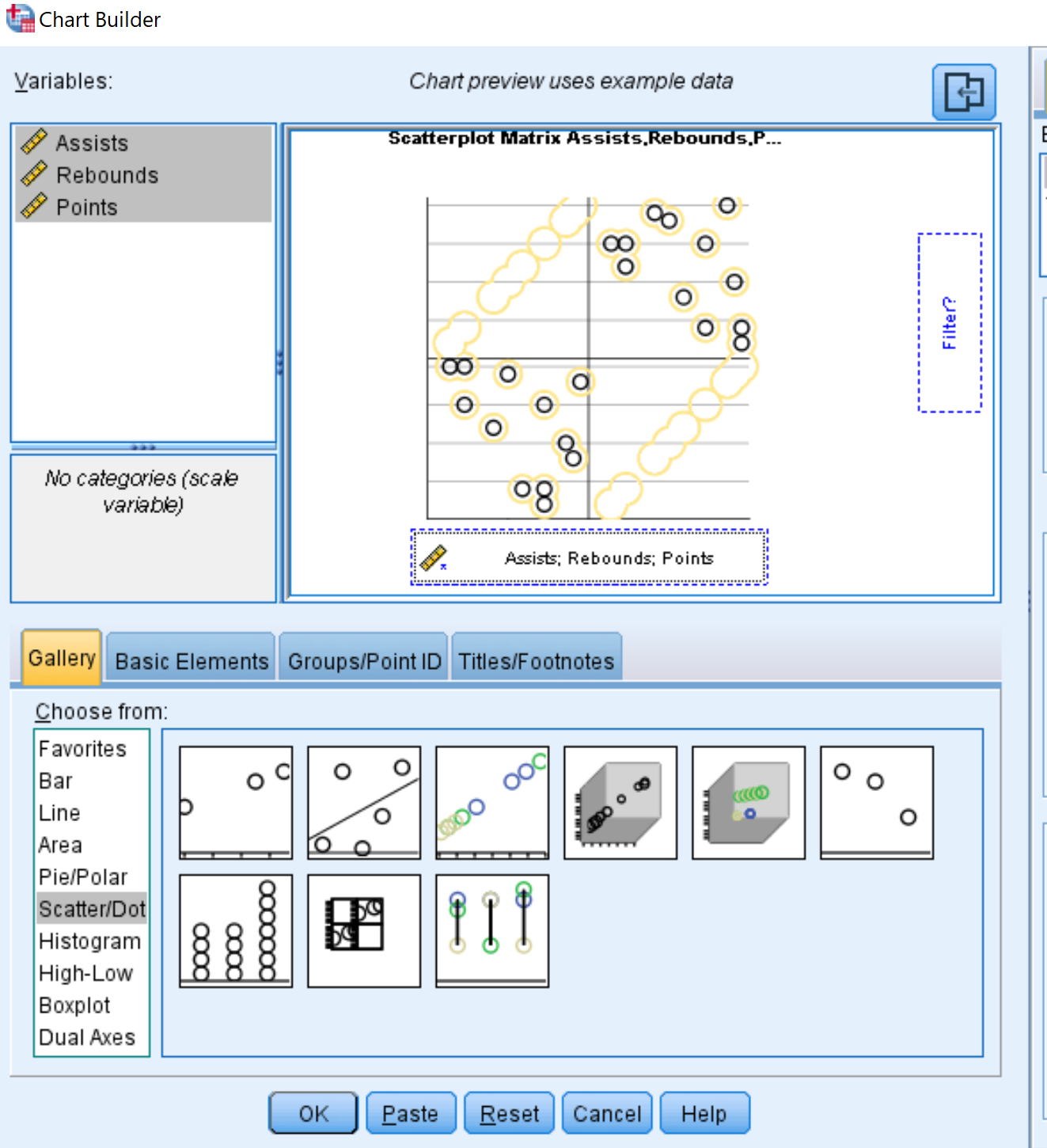
• चार्ट प्रकार के लिए, स्कैटर/प्वाइंट पर क्लिक करें।
• स्कैटरप्लॉट मैट्रिक्स कहने वाली छवि पर क्लिक करें।
• ऊपर बाईं ओर वेरिएबल बॉक्स में, Ctrl दबाए रखें और तीन वेरिएबल नामों पर क्लिक करें। उन्हें चार्ट के नीचे स्कैटरमैट्रिक्स वाले बॉक्स में खींचें।
• अंत में, OK पर क्लिक करें।

निम्नलिखित स्कैटरप्लॉट मैट्रिक्स स्वचालित रूप से दिखाई देगा:

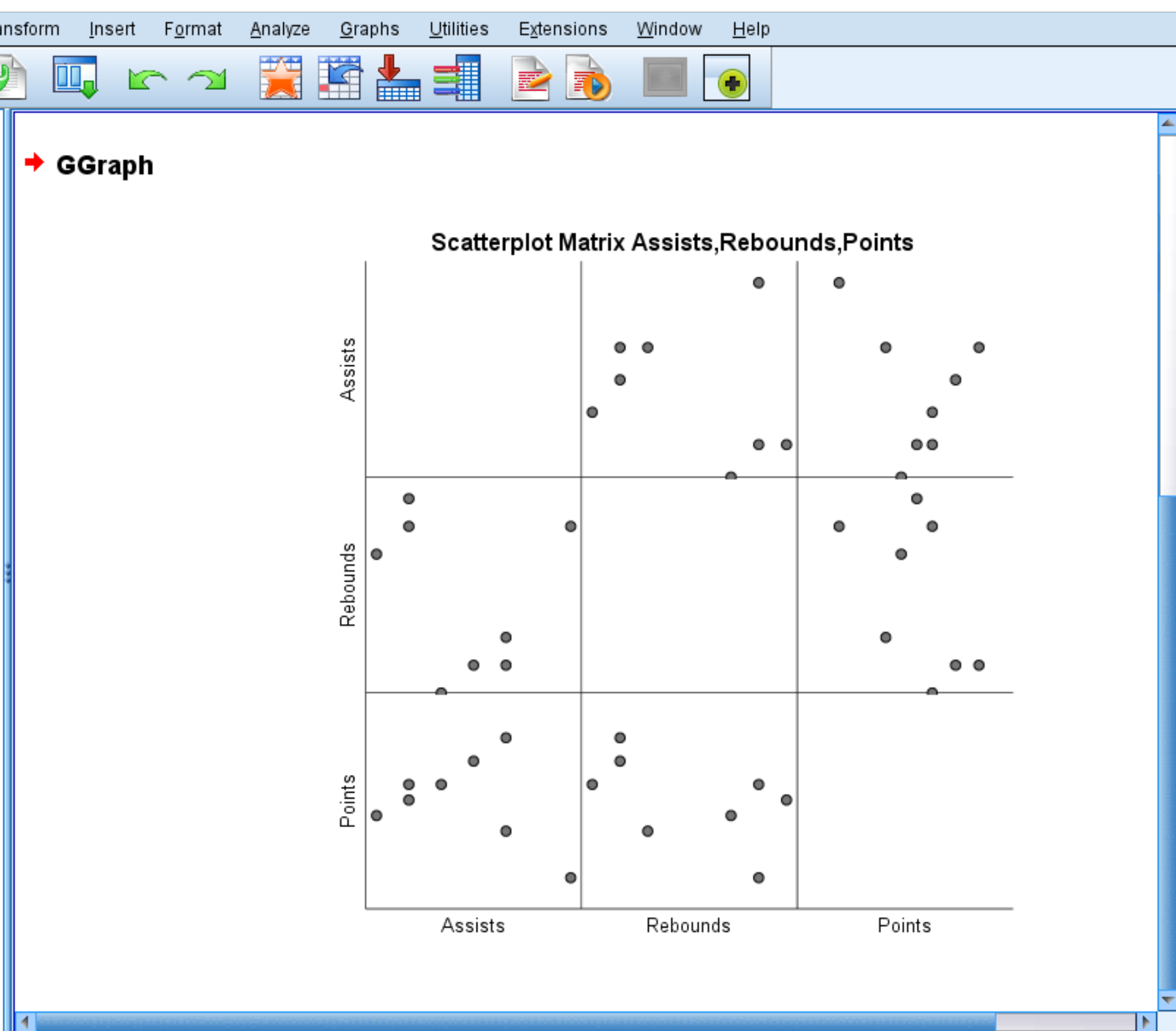
प्रत्येक व्यक्तिगत स्कैटरप्लॉट दो चरों के बीच जोड़ीवार संयोजन दिखाता है। उदाहरण के लिए, निचले बाएँ कोने में स्कैटर प्लॉट डेटासेट में 8 खिलाड़ियों में से प्रत्येक के लिए अंकों और सहायता के जोड़ीदार संयोजन को दर्शाता है।

स्कैटरप्लॉट मैट्रिक्स वैकल्पिक है, लेकिन यह डेटा सेट में चर के प्रत्येक जोड़ीदार संयोजन के बीच संबंध को देखने का एक अच्छा तरीका प्रदान करता है।