औसत प्रकार (सांख्यिकी)

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 आंकड़े शून्य टिप्पणियां

यहां हम बताते हैं कि सांख्यिकी में सभी प्रकार के औसत क्या हैं और उनकी गणना कैसे की जाती है। आपको प्रत्येक प्रकार की स्टॉकिंग के लिए सूत्र और उदाहरण मिलेंगे।

लेकिन यह देखने से पहले कि औसत कितने प्रकार के होते हैं, हमें तार्किक रूप से यह जानना होगा कि आंकड़ों में औसत क्या है। इसलिए, हम अनुशंसा करते हैं कि आप जारी रखने से पहले निम्नलिखित लिंक से परामर्श लें।

➤ देखें: औसत (सांख्यिकी) क्या है?

सांख्यिकी में औसत कितने प्रकार के होते हैं?

सांख्यिकी में, औसत के प्रकार हैं:

अंकगणित औसत
भारित औसत
ज्यामितीय साधन
मूल का अर्थ है वर्ग
हार्मोनिक अर्थ
सामान्यीकृत औसत
सामान्यीकृत एफ-औसत
छंटाई का मतलब है
अंतरचतुर्थक माध्य
किसी फ़ंक्शन का औसत

आगे हम बताएंगे कि सांख्यिकी में सभी प्रकार के औसतों की गणना कैसे करें। औसत के पांच सबसे अधिक उपयोग किए जाने वाले प्रकार अंकगणितीय औसत, भारित औसत, ज्यामितीय औसत, द्विघात औसत और हार्मोनिक औसत हैं। इसलिए हम इन पांच मुख्य प्रकार के मीडिया के बारे में अधिक विस्तार से जानेंगे।

अंकगणित औसत

अंकगणित माध्य की गणना सभी मानों को जोड़कर और फिर डेटा बिंदुओं की कुल संख्या से विभाजित करके की जाती है।

इसलिए अंकगणितीय औसत का सूत्र इस प्रकार है:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

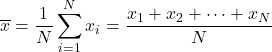
अंकगणितीय माध्य को अंकगणितीय माध्य के रूप में भी जाना जाता है।

अंकगणितीय औसत संभवतः सांख्यिकी में औसत का सबसे अधिक उपयोग किया जाने वाला प्रकार है।

इस प्रकार का औसत कैसे प्राप्त किया जाता है इसका एक उदाहरण देखने के लिए, हम निम्नलिखित डेटा के अंकगणितीय औसत की गणना करेंगे:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

अंकगणितीय माध्य की गणना करने के लिए, बस सभी सांख्यिकीय डेटा को जोड़ें और डेटा की कुल संख्या से विभाजित करें, जो 6 है:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

भारित औसत

भारित औसत की गणना करने के लिए, आपको पहले प्रत्येक सांख्यिकीय डेटा को उसके वजन (या वजन) से गुणा करना होगा, फिर सभी उत्पादों को जोड़ना होगा, और अंत में भारित योग को सभी भारों के योग से विभाजित करना होगा।

इसलिए भारित औसत सूत्र इस प्रकार है:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

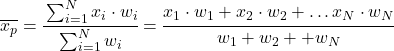
जहां x _i सांख्यिकीय मान है और w _i इसका संगत भार है।

भारित औसत को समझना अधिक कठिन है, इसलिए हम निम्नलिखित उदाहरण की जाँच करने की सलाह देते हैं जो चरण दर चरण बताता है कि इसकी गणना कैसे की जाती है:

➤ देखें: भारित औसत का उदाहरण

ज्यामितीय साधन

सांख्यिकीय डेटा के एक सेट का ज्यामितीय माध्य सभी मूल्यों के उत्पाद के nवें मूल के बराबर है।

इस प्रकार के औसत का उपयोग व्यवसाय वित्त में रिटर्न की दरों, प्रतिशत औसत और चक्रवृद्धि ब्याज की गणना के लिए किया जाता है।

इस प्रकार के भंडारण का सूत्र काफी जटिल है। वास्तव में, सभी सांख्यिकीय सेटों के ज्यामितीय माध्य की गणना नहीं की जा सकती है, लेकिन कभी-कभी इस प्रकार का माध्य निर्धारित नहीं किया जा सकता है। यही कारण है कि हम अनुशंसा करते हैं कि आप निम्नलिखित लिंक में बताए गए सभी अपवादों से परामर्श लें:

➤ देखें: ज्यामितीय माध्य सूत्र

मूल का अर्थ है वर्ग

मूल माध्य वर्ग डेटा के वर्गों के अंकगणितीय माध्य के वर्गमूल के बराबर है।

इसलिए माध्य वर्ग सूत्र इस प्रकार है:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

इस प्रकार के औसत को मूल माध्य वर्ग , मूल माध्य वर्ग या आरएमएस भी कहा जाता है।

आइए बस यह बताएं कि घन औसत भी मौजूद है, लेकिन इसका उपयोग बहुत विशेष मामलों में किया जाता है।

वर्ग औसत के फायदे और नुकसान हैं, उदाहरण के लिए, यह विशेष रूप से तब उपयोगी होता है जब सांख्यिकीय चर सकारात्मक और नकारात्मक मान लेता है, क्योंकि डेटा के प्रत्येक टुकड़े का वर्ग करने से, सभी मान सकारात्मक हो जाते हैं। आप निम्न लिंक पर क्लिक करके इस मीडिया प्रकार की अधिक विशेषताएं देख सकते हैं:

➤ देखें: मूल माध्य वर्ग के फायदे और नुकसान

हार्मोनिक अर्थ

हार्मोनिक माध्य की गणना सांख्यिकीय डेटा की कुल संख्या को प्रत्येक मान के व्युत्क्रमों के योग से विभाजित करके की जाती है।

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

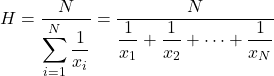
हार्मोनिक औसत का उपयोग औसत गति, समय की गणना करने या इलेक्ट्रॉनिक गणना करने के लिए किया जाता है। यह विशेषता हार्मोनिक औसत को अन्य प्रकार के औसत से अलग करती है, जिसका उपयोग अक्सर मूल्य औसत या प्रतिशत की गणना में किया जाता है।

आप इस प्रकार के औसत की गणना के उदाहरण निम्नलिखित पृष्ठ पर देख सकते हैं:

➤ देखें: हार्मोनिक अर्थ के उदाहरण

अन्य प्रकार के मोज़े

इस अनुभाग में हम अन्य प्रकार के स्टॉकिंग्स के लिए सूत्र देखेंगे। हम प्रत्येक प्रकार के बारे में विस्तार से नहीं बताएंगे क्योंकि उनका व्यापक रूप से उपयोग नहीं किया जाता है, लेकिन आपके लिए यह जानना अच्छा होगा कि अन्य प्रकार के स्टॉकिंग्स भी हैं।

सामान्यीकृत औसत ऊपर देखे गए औसत प्रकारों का मिश्रण है और इसकी गणना निम्नलिखित सूत्र का उपयोग करके की जाती है:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

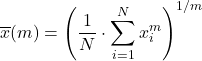
मान लीजिए कि f एक इंजेक्शन और मोनोटोनिक फ़ंक्शन है, तो सामान्यीकृत f-माध्य को इस प्रकार परिभाषित किया गया है:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

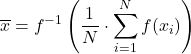
ट्रिम किए गए माध्य में नमूने के ऊपरी और निचले छोर पर टिप्पणियों का प्रतिशत घटाने के बाद अंकगणितीय माध्य की गणना करना शामिल है। दोनों सिरों पर समान प्रतिशत को अस्वीकार किया जाना चाहिए।

अंतरचतुर्थक माध्य की गणना करने के लिए, जिसे अंतरचतुर्थक माध्य भी कहा जाता है, पहले और चौथे चतुर्थक के डेटा को पहले हटा दिया जाता है, और फिर केवल नमूने के दूसरे और तीसरे चतुर्थक के अंकगणितीय माध्य की गणना की जाती है। इस प्रकार के औसत का सूत्र इस प्रकार है:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

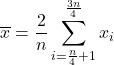
अंत में, आप किसी फ़ंक्शन का माध्य भी ज्ञात कर सकते हैं। एक बंद अंतराल [ए,बी] पर निरंतर फ़ंक्शन का औसत मूल्य निम्नलिखित सूत्र का उपयोग करके गणना की जाती है:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

नमूना और जनसंख्या औसत

अंत में, हम देखेंगे कि नमूना औसत और जनसंख्या औसत के बीच क्या अंतर है, दो प्रकार के औसत जो अक्सर भ्रमित होते हैं।

नमूना माध्य एक सांख्यिकीय नमूने के मूल्यों पर गणना किया गया औसत है, अर्थात इसकी गणना एक चर के सभी मूल्यों के हिस्से पर की जाती है।

जनसंख्या औसत एक सांख्यिकीय जनसंख्या पर गणना किया गया औसत है, अर्थात एक चर के सभी मूल्यों पर। इसलिए, जनसंख्या माध्य चर की गणितीय अपेक्षा से मेल खाता है।

यदि पर्याप्त मात्रा में डेटा ज्ञात हो तो नमूना माध्य को व्यावहारिक रूप से जनसंख्या माध्य के बराबर माना जा सकता है। लेकिन जनसंख्या माध्य का मान प्राप्त करना बहुत कठिन है, क्योंकि वास्तव में किसी वितरण के सभी मान शायद ही ज्ञात होते हैं।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने