सांख्यिकी में औसत क्यों महत्वपूर्ण है?

डेटा सेट का माध्य डेटा सेट के औसत मूल्य को दर्शाता है। इसकी गणना इस प्रकार की जाती है:

औसत = Σx _i / n

सोना:

• Σ: एक प्रतीक जिसका अर्थ है “योग”
• x _i : डेटा सेट में i ^वां अवलोकन
• n: डेटासेट में अवलोकनों की कुल संख्या

उदाहरण के लिए, मान लीजिए कि हमारे पास 11 अवलोकनों के साथ निम्नलिखित डेटासेट हैं:

डेटासेट: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

डेटासेट के औसत की गणना निम्नानुसार की जाती है:

औसत = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9.54

सांख्यिकी में, औसत निम्नलिखित कारणों से महत्वपूर्ण है:

1. औसत हमें यह अंदाज़ा देता है कि डेटा सेट का “केंद्र” कहाँ है।

2. जिस तरह से इसकी गणना की जाती है, उसके कारण औसत में डेटा सेट में प्रत्येक अवलोकन से जानकारी शामिल होती है।

निम्नलिखित उदाहरण इन दो कारणों को दर्शाता है।

उदाहरण: डेटा के एक सेट के औसत की गणना करें

मान लीजिए कि हमारे पास एक डेटासेट है जिसमें एक निश्चित शहर में 10,000 विभिन्न घरों की बिक्री कीमतें शामिल हैं।

कच्चे डेटा की हजारों पंक्तियों को देखने के बजाय, हम उस शहर में घरों की औसत बिक्री मूल्य को तुरंत समझने के लिए औसत मूल्य की गणना कर सकते हैं।

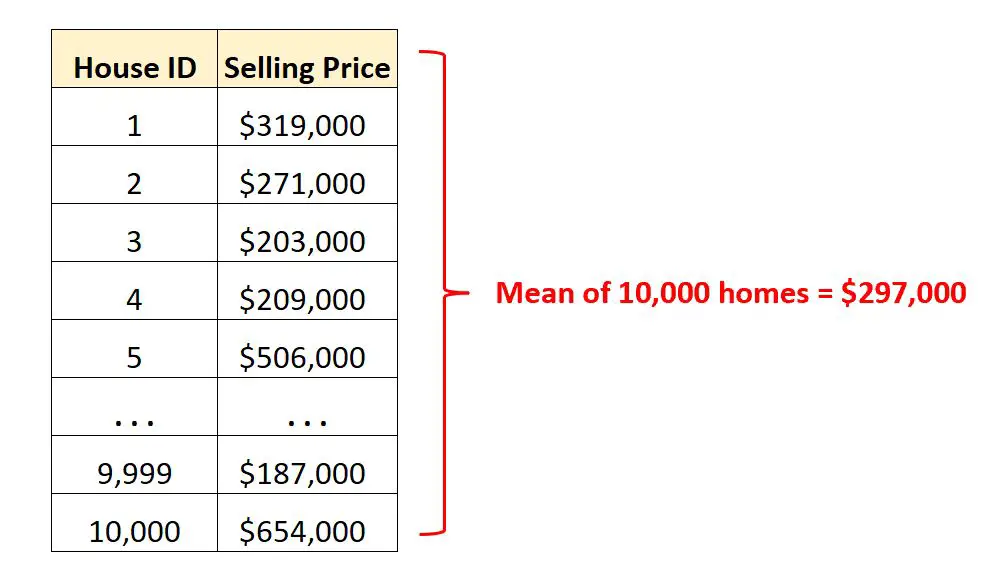
यह जानकर कि औसत बिक्री मूल्य $297,000 है, हमें यह अंदाज़ा मिलता है कि इस शहर में एक “सामान्य” घर कितने में बिकता है।

कच्चे डेटा की सभी पंक्तियों को देखने की तुलना में औसत के इस एकल मान की व्याख्या करना बहुत आसान है।

और चूंकि प्रत्येक घर की बिक्री मूल्य का उपयोग औसत की गणना करने के लिए किया गया था, हम उस शहर के सभी घरों की कुल बिक्री मूल्य जानने के लिए औसत बिक्री मूल्य को घरों की कुल संख्या से गुणा कर सकते हैं:

• सभी घरों का कुल बिक्री मूल्य = औसत बिक्री मूल्य * घरों की संख्या
• सभी घरों का कुल बिक्री मूल्य = $297,000 * 10,000
• सभी घरों का कुल बिक्री मूल्य = $2,970,000,000

हम देख सकते हैं कि इस शहर में सभी घरों की कुल बिक्री कीमत 2.97 बिलियन डॉलर है।

औसत का उपयोग कब करें

डेटा सेट का विश्लेषण करते समय, हम अक्सर यह समझना चाहते हैं कि केंद्रीय मूल्य कहाँ है।

आंकड़ों में, दो सामान्य मीट्रिक हैं जिनका उपयोग हम डेटा सेट के केंद्र को मापने के लिए करते हैं:

• माध्य : डेटा के एक सेट में औसत मूल्य
• माध्यिका : डेटा सेट में माध्यिका मान

औसत डेटा सेट के केंद्र को मापने का सबसे आम तरीका है, लेकिन यह वास्तव में निम्नलिखित स्थितियों में भ्रामक हो सकता है:

• जब वितरण असममित हो.
• जब वितरण में आउटलेर्स शामिल हों।

इसे स्पष्ट करने के लिए निम्नलिखित दो उदाहरणों पर विचार करें।

उदाहरण 1: विषम वितरण के माध्य की गणना करना

एक निश्चित शहर के निवासियों के वेतन के निम्नलिखित वितरण पर विचार करें:

वितरण के दाईं ओर उच्च मजदूरी माध्य को वितरण के केंद्र से दूर धकेल देती है।

इस प्रकार, औसत की तुलना में औसत एक निवासी के “सामान्य” वेतन को बेहतर ढंग से दर्शाता है, क्योंकि वितरण दाईं ओर झुका हुआ है।

इस विशेष उदाहरण में, औसत वेतन $47,000 है जबकि औसत वेतन $32,000 है।

इस प्रकार, औसत उस शहर में सामान्य वेतन का कहीं अधिक प्रतिनिधि है।

उदाहरण 2: आउटलेर्स की उपस्थिति में माध्य की गणना करना

निम्नलिखित ग्राफ़ पर विचार करें जो एक निश्चित सड़क पर घरों के वर्ग फ़ुटेज को दर्शाता है:

औसत कुछ बेहद बड़े घरों से काफी प्रभावित होता है, जबकि औसत नहीं होता है।

हम देख सकते हैं कि माध्यिका उस सड़क पर एक घर के “सामान्य” वर्ग फुटेज को औसत की तुलना में कैप्चर करने का बेहतर काम करती है, क्योंकि यह आउटलेर्स से प्रभावित नहीं होता है।

सारांश

यहां इस आलेख से मुख्य निष्कर्षों का संक्षिप्त सारांश दिया गया है:

• माध्य डेटा के एक सेट में औसत मान का प्रतिनिधित्व करता है।
• माध्य महत्वपूर्ण है क्योंकि यह हमें यह अंदाज़ा देता है कि डेटा सेट में केंद्रीय मान कहाँ स्थित है।
• माध्य इसलिए भी महत्वपूर्ण है क्योंकि इसमें डेटा सेट में प्रत्येक अवलोकन की जानकारी शामिल होती है।
• जब कोई डेटा सेट तिरछा हो या उसमें आउटलेर्स हों तो औसत भ्रामक हो सकता है। इन परिदृश्यों में, माध्यिका अधिक सटीक विचार देती है कि डेटा सेट का “केंद्र” कहाँ है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल अन्य वर्णनात्मक आँकड़ों पर अतिरिक्त जानकारी प्रदान करते हैं:

सांख्यिकी में माध्यिका क्यों महत्वपूर्ण है?
सांख्यिकी में मानक विचलन क्यों महत्वपूर्ण है?
माध्य बनाम माध्यिका का उपयोग कब करें