एकाधिक मानक विचलनों का माध्य कैसे ज्ञात करें

कभी-कभी आप दो या अधिक मानक विचलनों का औसत ज्ञात करना चाह सकते हैं।

ऐसा करने के लिए, आप अपने डेटा के आधार पर निम्नलिखित दो सूत्रों में से एक का उपयोग कर सकते हैं:

विधि 1: समान नमूना आकार

यदि आप k समूहों के बीच औसत मानक विचलन ज्ञात करना चाहते हैं और प्रत्येक समूह का नमूना आकार समान है, तो आप निम्न सूत्र का उपयोग कर सकते हैं:

औसत एसडी = √ (एस ₁ ² + एस ₂ ² +… + एस _के ² ) / के

सोना:

• _sk : ^kth समूह के लिए मानक विचलन
• k : समूहों की कुल संख्या

विधि 2: असमान नमूना आकार

यदि आप k समूहों के बीच औसत मानक विचलन ज्ञात करना चाहते हैं और प्रत्येक समूह का नमूना आकार समान नहीं है, तो आप निम्न सूत्र का उपयोग कर सकते हैं:

औसत SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – जे)

सोना:

• n _k : k ^वें समूह के लिए नमूना आकार
• _sk : ^kth समूह के लिए मानक विचलन
• k : समूहों की कुल संख्या

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में प्रत्येक सूत्र का उपयोग कैसे करें।

विधि 1: समान नमूना आकारों के लिए मानक विचलन के माध्य की गणना करना

मान लीजिए कि हम निम्नलिखित छह बिक्री अवधियों में बिक्री के औसत मानक विचलन की गणना करना चाहते हैं:

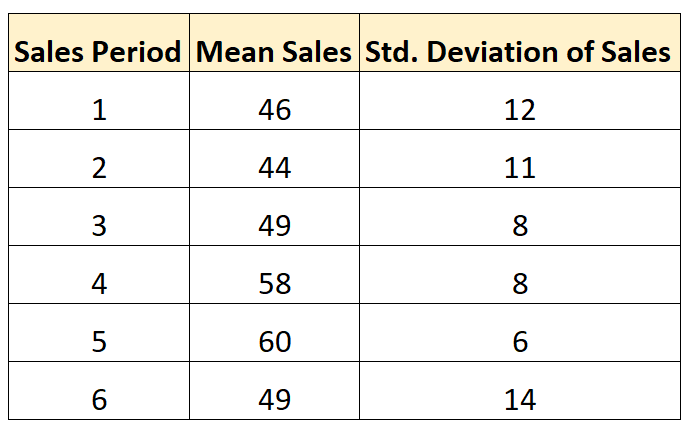
आइए मान लें कि हमने प्रत्येक बिक्री अवधि के दौरान समान संख्या में बिक्री लेनदेन किए। प्रति अवधि बिक्री के औसत मानक विचलन की गणना के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

• औसत मानक विचलन = √ (एस ₁ ² + एस ₂ ² + … + एस _के ² ) / के
• औसत मानक विचलन = √ (12 ² + 11 ² + 8 ² + 8 ² + 6 ² + 14 ² ) / 6
• औसत मानक विचलन = 10.21

प्रति अवधि बिक्री का औसत मानक विचलन 10.21 है।

विधि 2: असमान नमूना आकारों के लिए मानक विचलन का औसत

मान लीजिए कि हम निम्नलिखित छह बिक्री अवधियों में बिक्री के औसत मानक विचलन की गणना करना चाहते हैं:

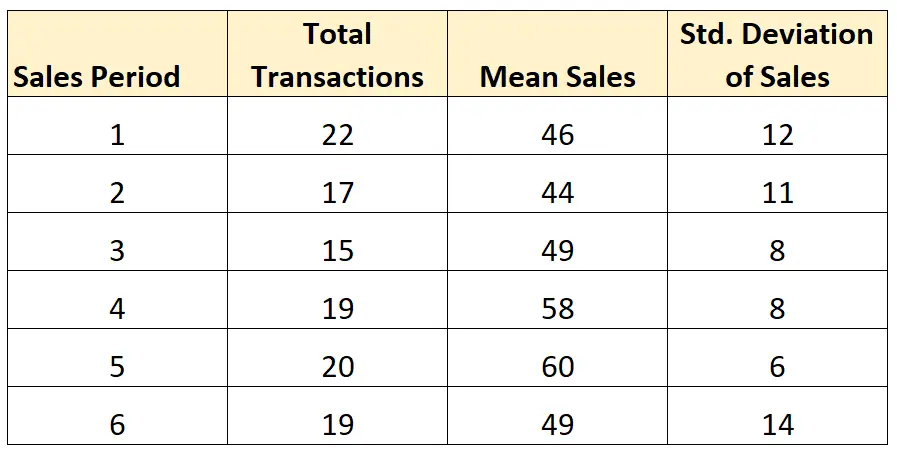
चूंकि नमूना आकार (कुल लेनदेन) प्रत्येक बिक्री अवधि में समान नहीं है, हम प्रति अवधि बिक्री के औसत मानक विचलन की गणना करने के लिए निम्नलिखित सूत्र का उपयोग करेंगे:

• औसत SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – जे)
• औसत एसडी = √ ((21)12 ² + (16)11 ² + (14)8 ² + (18)8 ² + (19)6 ² + (18)14 ² ) / 106
• माध्य एसडी = 10.29

प्रति अवधि बिक्री का औसत मानक विचलन 10.29 है।

ध्यान दें कि दोनों उदाहरणों में औसत मानक विचलन काफी समान था। ऐसा इसलिए है क्योंकि दूसरे उदाहरण में नमूना आकार (कुल लेनदेन) सभी एक-दूसरे के काफी करीब थे।

माध्य मानक विचलन की गणना करने की दो विधियाँ केवल तभी महत्वपूर्ण रूप से भिन्न होती हैं जब नमूना आकार समूहों के बीच काफी भिन्न होता है।