निचले वर्ग

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 2, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में न्यूनतम वर्ग क्या है, न्यूनतम वर्ग विधि क्या है, और एक प्रतिगमन मॉडल को न्यूनतम वर्ग मानदंड द्वारा कैसे फिट किया जाता है।

न्यूनतम वर्ग विधि क्या है?

न्यूनतम वर्ग विधि एक सांख्यिकीय विधि है जिसका उपयोग प्रतिगमन के समीकरण को निर्धारित करने के लिए किया जाता है। दूसरे शब्दों में, न्यूनतम वर्ग विधि एक मानदंड है जिसका उपयोग प्रतिगमन मॉडल में प्रतिगमन समीकरण की गणना करते समय प्राप्त त्रुटि को कम करने के लिए किया जाता है।

सीधे तौर पर, न्यूनतम वर्ग विधि में अवशेषों के वर्गों के योग को कम करना शामिल है, या दूसरे शब्दों में, यह प्रतिगमन मॉडल द्वारा अनुमानित मूल्यों और देखे गए मूल्यों के बीच अंतर के वर्गों के योग को कम करने पर आधारित है। . . नीचे हम विस्तार से देखेंगे कि एक प्रतिगमन मॉडल को न्यूनतम वर्ग मानदंड पर कैसे फिट किया जाता है।

न्यूनतम वर्ग विधि की मुख्य विशेषता यह है कि प्रेक्षित मानों और प्रतिगमन फ़ंक्शन के बीच की सबसे लंबी दूरी कम से कम हो जाती है। अन्य प्रतिगमन मानदंडों के विपरीत, न्यूनतम वर्ग विधि छोटे अवशेषों की तुलना में बड़े अवशेषों को कम करना अधिक महत्वपूर्ण मानती है, क्योंकि बड़ी संख्या का वर्ग छोटी संख्या के वर्ग से बहुत बड़ा होता है। संख्या।

अनुमान त्रुटि

न्यूनतम वर्ग की अवधारणा को पूरी तरह से समझने के लिए, हमें पहले यह स्पष्ट होना चाहिए कि प्रतिगमन मॉडल में अवशेष क्या हैं। इसलिए हम नीचे देखेंगे कि अनुमान त्रुटि क्या है और इसकी गणना कैसे की जाती है।

आंकड़ों में, अनुमान त्रुटि , जिसे अवशिष्ट भी कहा जाता है, वास्तविक मान और प्रतिगमन मॉडल द्वारा फिट किए गए मान के बीच का अंतर है। इसलिए एक सांख्यिकीय अवशेष की गणना इस प्रकार की जाती है:

$e_i=y_i-\widehat{y}_i$

सोना:

$e_i$

डेटा का अवशेष है I
$y_i$

डेटा का वास्तविक मूल्य है I
$\widehat{y}_i$

डेटा i के लिए प्रतिगमन मॉडल द्वारा प्रदान किया गया मान है।

इस प्रकार, डेटा के एक टुकड़े का अवशेष जितना बड़ा होगा, प्रतिगमन मॉडल उतना ही खराब डेटा के इस टुकड़े के लिए अनुकूलित होगा। इस प्रकार, अवशिष्ट जितना छोटा होगा, उसके वास्तविक मूल्य और अनुमानित मूल्य के बीच की दूरी उतनी ही कम होगी।

इसी तरह, यदि डेटा के किसी टुकड़े का अवशेष सकारात्मक है, तो इसका मतलब है कि प्रतिगमन मॉडल वास्तविक मूल्य से कम मूल्य की भविष्यवाणी करता है। जबकि यदि अवशिष्ट नकारात्मक है, तो इसका मतलब है कि अनुमानित मूल्य वास्तविक मूल्य से अधिक है।

त्रुटि वर्ग न्यूनतम करें

अब जब हम जानते हैं कि आंकड़ों में अवशिष्ट क्या है, तो यह समझना आसान हो जाएगा कि त्रुटि वर्गों को कैसे कम किया जाता है।

किसी त्रुटि का वर्ग अवशिष्ट का वर्ग होता है, इसलिए त्रुटि का वर्ग वास्तविक मान और प्रतिगमन मॉडल द्वारा दो की घात तक बढ़ाए गए मान के बीच के अंतर के बराबर होता है।

$e_i^2=(y_i-\widehat{y}_i)^2$

सोना:

$e_i^2$

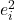
डेटा के अवशेष का वर्ग है I.
$y_i$

डेटा का वास्तविक मूल्य है I
$\widehat{y}_i$

डेटा i के लिए प्रतिगमन मॉडल द्वारा प्रदान किया गया मान है।

इस प्रकार, न्यूनतम वर्ग विधि में त्रुटियों के वर्गों के योग को कम करके एक प्रतिगमन मॉडल बनाना शामिल है। इसलिए न्यूनतम वर्ग मानदंड निम्नलिखित अभिव्यक्ति के न्यूनतमकरण पर आधारित है:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

यही कारण है कि न्यूनतम वर्ग मानदंड को न्यूनतम वर्ग मानदंड भी कहा जाता है।

जैसा कि आप पिछले सूत्र में देख सकते हैं, न्यूनतम वर्ग मानदंड छोटे अवशेषों की तुलना में बड़े अवशेषों को कम करने को अधिक महत्व देता है। उदाहरण के लिए, यदि एक अवशेष 3 है और दूसरा अवशेष 5 है, तो उनके वर्ग क्रमशः 9 और 25 हैं, इसलिए न्यूनतम वर्ग मानदंड पहले अवशेष से पहले दूसरे अवशेष को कम करने को प्राथमिकता देगा।

न्यूनतम वर्ग समायोजन

न्यूनतम वर्ग मानदंड का उपयोग करके एक प्रतिगमन मॉडल को फिट करने में एक प्रतिगमन मॉडल ढूंढना शामिल है जो अवशेषों के वर्गों को न्यूनतम करता है। इसलिए, प्रतिगमन मॉडल से प्राप्त समीकरण वह होगा जिसके देखे गए मानों और फिट किए गए मानों के बीच अंतर का वर्ग न्यूनतम हो।

निम्नलिखित उदाहरण में ध्यान दें कि प्रतिगमन मॉडल बनाने के लिए अधिक मानदंड हैं और, चुने गए मानदंड के आधार पर, प्रतिगमन समीकरण भिन्न होता है।

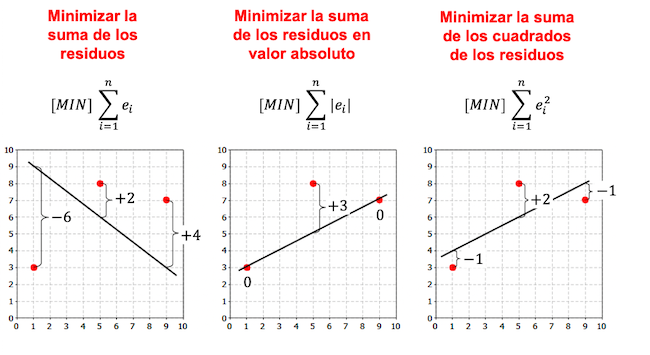
जैसा कि आप पिछले उदाहरणों में देख सकते हैं, समान डेटा सेट के लिए रैखिक प्रतिगमन मॉडल से प्राप्त रेखा चुने हुए मानदंड पर निर्भर करती है। आम तौर पर, प्रतिगमन मॉडल में न्यूनतम वर्ग मानदंड का उपयोग किया जाता है।

आंकड़ों में, सबसे व्यापक रूप से इस्तेमाल किया जाने वाला प्रतिगमन मॉडल सरल रैखिक प्रतिगमन मॉडल है, जिसमें एक सीधी रेखा का उपयोग करके स्वतंत्र चर X और आश्रित चर Y के बीच संबंध का अनुमान लगाना शामिल है।

$y=b_0+b_1x$

तो, डेटा सेट को एक सरल रैखिक प्रतिगमन मॉडल में फिट करने के सूत्र हैं:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

आप निम्न लिंक पर क्लिक करके एक उदाहरण देख सकते हैं कि न्यूनतम वर्ग मानदंड का उपयोग करके एक सरल रैखिक प्रतिगमन मॉडल की गणना कैसे की जाती है:

➤ देखें: सरल रैखिक प्रतिगमन का उदाहरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने