केंद्रीय प्रवृत्ति के माप: परिभाषा एवं उदाहरण
केंद्रीय प्रवृत्ति का माप एक एकल मान है जो डेटा सेट के केंद्रीय बिंदु का प्रतिनिधित्व करता है। इस मान को डेटा सेट का “केंद्रीय स्थान” भी कहा जा सकता है।
सांख्यिकी में, केंद्रीय प्रवृत्ति के तीन सामान्य उपाय हैं:
- औसत
- मध्यस्थ
- वह रीति
इनमें से प्रत्येक उपाय विभिन्न तरीकों का उपयोग करके डेटा सेट के केंद्रीय स्थान का पता लगाता है। आप जिस प्रकार के डेटा का विश्लेषण कर रहे हैं उसके आधार पर, अन्य दो के बजाय इन तीन मैट्रिक्स में से एक का उपयोग करना बेहतर हो सकता है।
इस लेख में, हम देखेंगे कि केंद्रीय प्रवृत्ति के तीन मापों में से प्रत्येक की गणना कैसे करें और साथ ही यह कैसे निर्धारित करें कि आपके डेटा के आधार पर कौन सा माप उपयोग करना सबसे अच्छा है।
केन्द्रीय प्रवृत्ति के माप उपयोगी क्यों हैं?
इससे पहले कि हम देखें कि माध्य, माध्यिका और बहुलक की गणना कैसे करें, यह समझना उपयोगी है कि ये माप वास्तव में उपयोगी क्यों हैं।
निम्नलिखित परिदृश्य पर विचार करें:
एक युवा जोड़ा यह तय करने की कोशिश कर रहा है कि नए शहर में अपना पहला घर कहां खरीदा जाए और वे अधिकतम 150,000 डॉलर खर्च कर सकते हैं। शहर के कुछ क्षेत्रों में महंगे घर हैं, कुछ में सस्ते घर हैं, और कुछ में मध्यम कीमत के घर हैं। वे अपनी खोज को आसानी से उन विशिष्ट पड़ोसों तक सीमित करना चाहते हैं जो उनके बजट में फिट हों।
यदि दम्पति केवल प्रत्येक पड़ोस में एकल-परिवार के घरों की कीमतों को देखें, तो उन्हें यह निर्धारित करने में कठिनाई हो सकती है कि कौन सा पड़ोस उनके बजट के लिए सबसे उपयुक्त है, क्योंकि उन्हें कुछ इस तरह दिखाई दे सकता है:
पड़ोस में एक घर की कीमतें: $140,000, $190,000, $265,000, $115,000, $270,000, $240,000, $250,000, $180,000, $160,000, $200,000, $240,000, $280,000,…
पड़ोस बी घर की कीमतें: $140,000, $290,000, $155,000, $165,000, $280,000, $220,000, $155,000, $185,000, $160,000, $200,000, $190,000, $140,000, $145.0 0 0,…
पड़ोस सी घर की कीमतें: $140,000, $130,000, $165,000, $115,000, $170,000, $100,000, $150,000, $180,000, $190,000, $120,000, $110,000, $130,000, $120,0 0 0,…
हालाँकि, यदि उन्हें प्रत्येक पड़ोस में घरों की औसत कीमत (उदाहरण के लिए केंद्रीय प्रवृत्ति का एक माप) पता होती, तो वे अपनी खोज को और अधिक तेज़ी से परिष्कृत कर सकते थे क्योंकि वे अधिक आसानी से पहचान सकते थे कि किस पड़ोस में घर की कीमतें उनके बजट से मेल खाती हैं:
पड़ोस A में एक घर की औसत कीमत: $220,000
पड़ोस बी में एक घर की औसत कीमत: $190,000
पड़ोस C में एक घर की औसत कीमत: $140,000
प्रत्येक पड़ोस में घर की औसत कीमत जानकर, वे तुरंत देख सकते हैं कि पड़ोस सी में उनके बजट के भीतर सबसे अधिक घर उपलब्ध होने की संभावना है।
केंद्रीय प्रवृत्ति के माप का उपयोग करने का यह लाभ है: यह आपको डेटा सेट के केंद्रीय मूल्य को समझने में मदद करता है, जो यह वर्णन करता है कि डेटा मान आम तौर पर कहां स्थित हैं। इस विशेष उदाहरण में, यह युवा जोड़े को प्रत्येक पड़ोस में एक घर की विशिष्ट कीमत को समझने में मदद करता है।
टेकअवे: केंद्रीय प्रवृत्ति का माप उपयोगी है क्योंकि यह हमें एक एकल मान प्रदान करता है जो डेटा सेट के “केंद्र” का वर्णन करता है। यह हमें डेटा सेट में सभी व्यक्तिगत मूल्यों को देखने की तुलना में डेटा सेट को बहुत तेजी से समझने में मदद करता है।
अर्थ
केंद्रीय प्रवृत्ति का सबसे अधिक उपयोग किया जाने वाला माप माध्य है। किसी डेटा सेट के औसत की गणना करने के लिए, बस सभी व्यक्तिगत मानों को जोड़ें और मानों की कुल संख्या से विभाजित करें।
औसत = (सभी मानों का योग) / (मानों की कुल संख्या)
उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित डेटा सेट है जो एक सीज़न के दौरान एक ही टीम के 10 बेसबॉल खिलाड़ियों द्वारा मारे गए घरेलू रनों की संख्या दिखाता है:
| खिलाड़ी | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #दस |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
प्रति खिलाड़ी हिट होम रन की औसत संख्या की गणना निम्नानुसार की जा सकती है:
औसत = (8+15+22+21+12+9+11+27+14+13) / 10 = 15.2 सर्किट ।
मंझला
माध्यिका डेटा सेट का मध्य मान है। आप डेटा सेट में सभी व्यक्तिगत मानों को सबसे छोटे से सबसे बड़े तक क्रमबद्ध करके और माध्य मान ज्ञात करके माध्यिका ज्ञात कर सकते हैं। यदि मानों की संख्या विषम है, तो माध्यिका मध्य मान है। यदि मानों की संख्या सम है, तो माध्यिका दो मध्य मानों का औसत है।
उदाहरण के लिए, पिछले उदाहरण में 10 बेसबॉल खिलाड़ियों द्वारा मारे गए घरेलू रनों की औसत संख्या का पता लगाने के लिए, हम खिलाड़ियों को हिट किए गए घरेलू रनों की संख्या के अवरोही क्रम में रैंक कर सकते हैं:
| खिलाड़ी | #1 | #6 | #7 | #5 | #दस | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
चूँकि हमारे पास मानों की संख्या सम है, माध्यिका केवल दो मध्य मानों का औसत है: 13.5 ।
इसके बजाय, विचार करें कि क्या हमारे पास नौ खिलाड़ी थे:
| खिलाड़ी | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
इस मामले में, चूँकि हमारे पास विषम संख्या में मान हैं, माध्यिका केवल मध्य मान है: 14 ।
वह रीति
मोड वह मान है जो डेटा सेट में सबसे अधिक बार दिखाई देता है। एक डेटा सेट में कोई मोड नहीं हो सकता है (यदि कोई मान दोहराता नहीं है), एक मोड, या एकाधिक मोड।
उदाहरण के लिए, निम्नलिखित डेटासेट में कोई मोड नहीं है:
| खिलाड़ी | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #दस |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
निम्नलिखित डेटासेट में एक मोड है: 15 । यह वह मान है जो सबसे अधिक बार दिखाई देता है.
| खिलाड़ी | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #दस |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
निम्नलिखित डेटासेट में तीन मोड हैं: 8, 15, 19 । ये वे मान हैं जो सबसे अधिक बार दिखाई देते हैं।
| खिलाड़ी | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #दस |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
श्रेणीबद्ध डेटा के साथ काम करते समय मोड केंद्रीय प्रवृत्ति का एक विशेष रूप से उपयोगी माप हो सकता है, क्योंकि यह हमें बताता है कि कौन सी श्रेणी सबसे अधिक बार दिखाई देती है। उदाहरण के लिए, निम्नलिखित बार चार्ट पर विचार करें जो लोगों के पसंदीदा रंग के बारे में सर्वेक्षण के परिणाम दिखाता है:
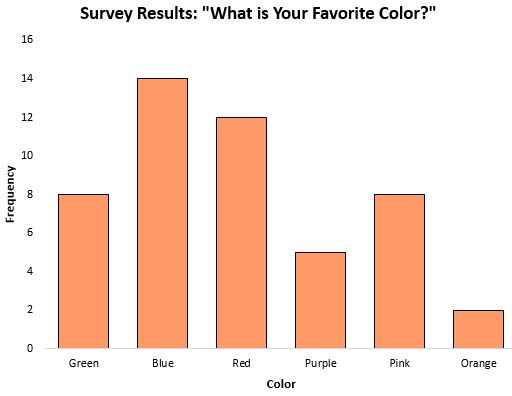
मोड , या प्रतिक्रिया जो सबसे अधिक बार हुई, नीला था।
ऐसे परिदृश्यों में जहां डेटा श्रेणीबद्ध है (जैसा कि ऊपर दिया गया है), माध्यिका या माध्य की गणना करना भी संभव नहीं है, इसलिए मोड केंद्रीय प्रवृत्ति का एकमात्र माप है जिसका हम उपयोग कर सकते हैं।
मोड का उपयोग संख्यात्मक डेटा के लिए भी किया जा सकता है, जैसा कि हमने बेसबॉल खिलाड़ियों के साथ उपरोक्त उदाहरण में देखा था। हालाँकि, “इस डेटा सेट के लिए एक विशिष्ट मान क्या है?” प्रश्न का उत्तर देने के लिए मोड कम उपयोगी होता है। »
उदाहरण के लिए, मान लीजिए कि हम इस टीम के किसी बेसबॉल खिलाड़ी द्वारा मारे गए घरेलू रनों की सामान्य संख्या जानना चाहते हैं:
| खिलाड़ी | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #दस |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
इस डेटासेट का मोड 8, 15, और 19 है क्योंकि ये सबसे अधिक बार आने वाले मान हैं। हालाँकि, ये टीम में किसी खिलाड़ी द्वारा मारे गए घरेलू रनों की सामान्य संख्या को समझने में बहुत मददगार नहीं हैं। इस मामले में केंद्रीय प्रवृत्ति का बेहतर माप माध्यिका (15) या माध्य (15 भी) होगा।
जब यह एक ऐसी संख्या होती है जो शेष मानों से बहुत दूर होती है तो यह बहुलक केंद्रीय प्रवृत्ति का भी एक खराब माप है। उदाहरण के लिए, निम्नलिखित डेटा सेट का मोड 30 है, लेकिन यह वास्तव में टीम में प्रति खिलाड़ी होम रन की “सामान्य” संख्या का प्रतिनिधित्व नहीं करता है:
| खिलाड़ी | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #दस |
|---|---|---|---|---|---|---|---|---|---|---|
| होम रन | 5 | 6 | 7 | दस | 11 | 12 | 13 | 15 | 30 | 30 |
फिर, माध्य या माध्यिका इस डेटा सेट के केंद्रीय स्थान का वर्णन करने का बेहतर काम करेगी।
माध्य, माध्यिका और मोड का उपयोग कब करें
हमने देखा है कि माध्य, माध्यिका और मोड सभी डेटा सेट के केंद्रीय स्थान, या “विशिष्ट मान” को बहुत अलग तरीकों से मापते हैं:
औसत: डेटा सेट में औसत मान ढूँढता है।
माध्यिका: डेटा सेट में माध्यिका मान ढूँढता है।
मोड: डेटा सेट में सबसे लगातार मान ढूँढता है।
यहां ऐसे परिदृश्य हैं जिनमें केंद्रीय प्रवृत्ति के कुछ उपायों का उपयोग दूसरों की तुलना में बेहतर है:
औसत का उपयोग कब करें
जब डेटा वितरण काफी सममित हो और कोई आउटलेयर न हो तो औसत का उपयोग करना सबसे अच्छा होता है।
उदाहरण के लिए, मान लीजिए कि हमारे पास निम्नलिखित वितरण है जो एक निश्चित शहर में व्यक्तियों के वेतन को दर्शाता है:

चूंकि यह वितरण काफी सममित है (यानी यदि आप इसे आधे में विभाजित करते हैं, तो प्रत्येक आधा लगभग बराबर दिखेगा) और इसमें कोई आउटलेयर नहीं है (यानी (बहुत अधिक वेतन नहीं), औसत इस डेटा सेट का वर्णन करने का अच्छा काम करेगा।
औसत $63,000 निकलता है, जो मोटे तौर पर वितरण के केंद्र में है:

माध्यिका का उपयोग कब करें
जब डेटा वितरण विषम हो या आउटलेयर हों तो माध्यिका का उपयोग करना सबसे अच्छा होता है।
पक्षपातपूर्ण डेटा:
जब वितरण विषम होता है, तब भी माध्यिका केंद्रीय स्थान पर कब्जा करने में सफल रहती है। उदाहरण के लिए, एक निश्चित शहर में व्यक्तियों के वेतन के निम्नलिखित वितरण पर विचार करें:

माध्य औसत की तुलना में किसी व्यक्ति के “सामान्य” वेतन को बेहतर ढंग से दर्शाता है। ऐसा इसलिए है क्योंकि वितरण के अंत में बड़े मान माध्य को केंद्र से दूर और लंबी पूंछ की ओर ले जाते हैं।
इस विशेष उदाहरण में, औसत हमें बताता है कि इस शहर में एक सामान्य व्यक्ति प्रति वर्ष लगभग $47,000 कमाता है, जबकि औसत हमें बताता है कि सामान्य व्यक्ति प्रति वर्ष केवल लगभग $32,000 कमाता है, जो कि सामान्य व्यक्ति का कहीं अधिक प्रतिनिधि है।
आउटलाइर्स:
जब डेटा में आउटलेयर होते हैं तो माध्यिका वितरण के केंद्रीय स्थान को बेहतर ढंग से पकड़ने में मदद करती है। उदाहरण के लिए, निम्नलिखित ग्राफ़ पर विचार करें जो एक निश्चित सड़क पर घरों के वर्ग फ़ुटेज को दर्शाता है:

औसत कुछ बेहद बड़े घरों से काफी प्रभावित होता है, जबकि औसत नहीं होता है। इस प्रकार, औसत की तुलना में माध्य उस सड़क पर एक घर के “सामान्य” वर्ग फुटेज को कैप्चर करने का बेहतर काम करता है।
मोड का उपयोग कब करें
इस मोड का सबसे अच्छा उपयोग तब किया जाता है जब आप श्रेणीबद्ध डेटा के साथ काम कर रहे हों और जानना चाहते हों कि कौन सी श्रेणी सबसे अधिक बार दिखाई देती है। यहां कुछ उदाहरण दिए गए हैं:
- आप लोगों के पसंदीदा रंगों पर एक सर्वेक्षण कर रहे हैं और जानना चाहते हैं कि प्रतिक्रियाओं में कौन सा रंग सबसे अधिक बार दिखाई देता है।
- आप वेबसाइट डिज़ाइन के लिए तीन विकल्पों में से लोगों की प्राथमिकताओं का सर्वेक्षण कर रहे हैं और जानना चाहते हैं कि लोग कौन सा डिज़ाइन सबसे अधिक पसंद करते हैं।
जैसा कि पहले उल्लेख किया गया है, यदि आप श्रेणीबद्ध डेटा के साथ काम कर रहे हैं, तो मध्यिका या माध्य की गणना करना भी संभव नहीं है, जो मोड को केंद्रीय प्रवृत्ति के एकमात्र माप के रूप में छोड़ देता है।
सामान्य तौर पर, यदि आप संख्यात्मक डेटा जैसे कि घरों के वर्ग फुटेज, प्रति खिलाड़ी हिट होम रन की संख्या, प्रति व्यक्ति वेतन आदि के साथ काम कर रहे हैं, तो आमतौर पर “सामान्य” मूल्य का वर्णन करने के लिए माध्यिका या औसत का उपयोग करना सबसे अच्छा होता है। डेटासेट.
नोट: यह ध्यान रखना महत्वपूर्ण है कि यदि कोई डेटा सेट पूरी तरह से सामान्य रूप से वितरित किया जाता है, तो माध्य, माध्यिका और मोड सभी का मान समान होता है।