खुला वितरण क्या है?

आंकड़ों में, एक खुला वितरण एक आवृत्ति वितरण है जिसमें एक या अधिक वर्ग (या “डिब्बे”) खुले होते हैं।

उदाहरण के लिए, निम्नलिखित आवृत्ति वितरण एक खुले वितरण का प्रतिनिधित्व करता है जिसमें सबसे छोटा वर्ग खुला है:

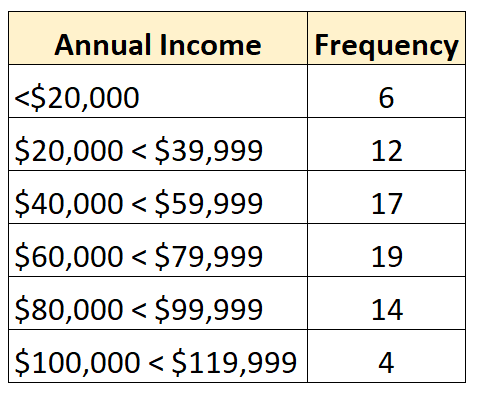
और निम्नलिखित आवृत्ति वितरण एक खुला वितरण दिखाता है जिसमें सबसे बड़ा वर्ग खुला है:

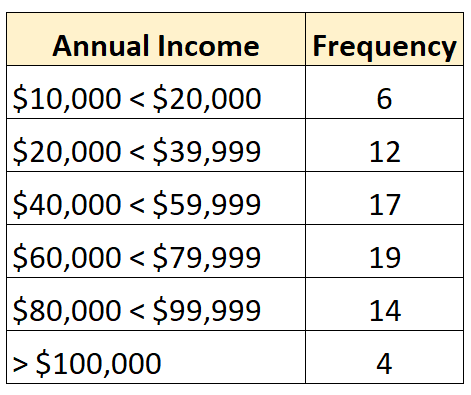
इसके विपरीत, एक बंद वितरण वह होता है जिसमें आवृत्ति वितरण के प्रत्येक वर्ग की एक ऊपरी और निचली सीमा होती है, जैसे कि निम्नलिखित:

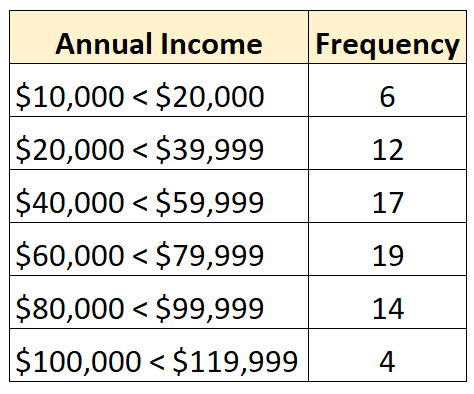
खुले वितरण का क्या कारण है?

खुला वितरण अक्सर शोधकर्ताओं द्वारा इस तरह से डेटा एकत्र करने का परिणाम होता है कि कक्षाओं में से एक खुला हो जाता है।

उदाहरण के लिए, मान लीजिए कि एक शोधकर्ता एक निश्चित शहर के निवासियों का सर्वेक्षण करता है और उनसे उनकी वार्षिक घरेलू आय के बारे में पूछता है।

शोधकर्ता “>$100,000” का व्यापक संभव उत्तर देना चुन सकते हैं क्योंकि वे जानते हैं कि उच्च आय वाले निवासी यह साझा करने में सहज नहीं होंगे कि वे कितना कमाते हैं यदि यह $100,000 से काफी अधिक है।

इसके विपरीत, शोधकर्ता यथासंभव संक्षिप्त उत्तर देने का विकल्प चुन सकता है क्योंकि वह जानता है कि जो निवासी बहुत कम कमाते हैं, वे जो कम कमाते हैं उसे साझा करने में भी सहज नहीं होंगे।

संक्षेप में, शोधकर्ता अक्सर अपने सर्वेक्षणों में खुले पाठ्यक्रम शामिल करते हैं क्योंकि वे उन लोगों की संख्या को अधिकतम करना चाहते हैं जो सर्वेक्षण प्रश्नों का उत्तर देने में सहज महसूस करते हैं।

खुले वितरण की समस्या

खुले वितरण के साथ समस्या यह है कि वास्तविक डेटा सेंसर किया जाता है। दूसरे शब्दों में, हम एक निश्चित शहर में $100,000 से अधिक कमाने वाले लोगों की संख्या जान सकते हैं, लेकिन वास्तव में हम उनकी सटीक वार्षिक आय नहीं जानते हैं।

यह संभव है कि कुछ लोग $150,000, $250,000, $500,000 या इससे भी अधिक कमाते हैं, लेकिन हमें कोई अंदाज़ा नहीं है क्योंकि इनमें से प्रत्येक व्यक्ति जांच में यह संकेत नहीं दे सकता है कि वे “>$100,000” कमाते हैं।

चूंकि डेटा को खुले वितरण में सेंसर किया गया है, हम डेटासेट में मूल्यों के सटीक माध्य और मानक विचलन की गणना करने में भी असमर्थ हैं क्योंकि हमारे पास कच्चे डेटा में सभी मूल्यों तक पहुंच नहीं है।

खुले वितरण का विश्लेषण कैसे करें

चूँकि हम खुले वितरण के सटीक माध्य की गणना नहीं कर सकते हैं, हम अक्सर डेटा सेट के “केंद्र” के माप के रूप में माध्यिका का उपयोग करते हैं।

याद रखें कि माध्यिका डेटा सेट के मध्य मान का प्रतिनिधित्व करती है।

खुले वितरण के साथ काम करते समय, हम माध्यिका का सर्वोत्तम अनुमान खोजने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:

माध्यिका का सर्वोत्तम अनुमान: L + ((n/2 – F) / f) * w

सोना:

• एल: मध्य समूह की निचली सीमा
• n: अवलोकनों की कुल संख्या
• एफ: मध्य समूह तक संचयी आवृत्ति
• एफ: मध्य समूह की आवृत्ति
• w: मध्य समूह की चौड़ाई

उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित खुला वितरण है:

डेटासेट में कुल 72 मान हैं। तो, हम जानते हैं कि औसत मान डेटासेट में 36वें और 37वें सबसे बड़े मानों के बीच होगा। इनमें से प्रत्येक मान “$60,000 – $79,999” वर्ग में आता है, इसलिए हम जानते हैं कि औसत आय उस सीमा में है।

माध्यिका का हमारा सर्वोत्तम अनुमान होगा:

औसत: 60,000 + ((72/2 – 25) / 19) * 19,999 = $71,578

यह मान इस डेटासेट में व्यक्तियों की औसत वार्षिक आय के हमारे सर्वोत्तम अनुमान का प्रतिनिधित्व करता है।