गामा वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि गामा वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इस प्रकार, आपको गामा वितरण की परिभाषा, इसके गुण और इसका ग्राफिक प्रतिनिधित्व कैसा दिखता है, यह पता चलेगा।

गामा वितरण क्या है?

गामा वितरण एक सतत संभाव्यता वितरण है जो दो विशिष्ट मापदंडों, α और λ द्वारा परिभाषित है। दूसरे शब्दों में, गामा वितरण इसके दो मापदंडों के मूल्य पर निर्भर करता है: α आकार पैरामीटर है और λ स्केल पैरामीटर है।

गामा वितरण का प्रतीक बड़ा ग्रीक अक्षर Γ है। इसलिए, यदि कोई यादृच्छिक चर गामा वितरण का अनुसरण करता है, तो इसे इस प्रकार लिखा जाता है:

$X\sim \Gamma(\alpha,\lambda)$

गामा वितरण को आकार पैरामीटर k = α और व्युत्क्रम स्केल पैरामीटर θ = 1/λ का उपयोग करके भी मानकीकृत किया जा सकता है। सभी मामलों में, गामा वितरण को परिभाषित करने वाले दो पैरामीटर सकारात्मक वास्तविक संख्याएं हैं।

आमतौर पर, गामा वितरण का उपयोग दाएं-तिरछे डेटा सेट को मॉडल करने के लिए किया जाता है, ताकि ग्राफ़ के बाईं ओर डेटा की अधिक सांद्रता हो। उदाहरण के लिए, गामा वितरण का उपयोग विद्युत घटकों की विश्वसनीयता को मॉडल करने के लिए किया जाता है।

गामा वितरण आरेख

गामा वितरण का ग्राफ उसके विशिष्ट मापदंडों के मूल्यों पर निर्भर करता है। नीचे आप देख सकते हैं कि गामा वितरण का घनत्व कार्य आकार पैरामीटर और स्केल पैरामीटर के आधार पर कैसे भिन्न होता है।

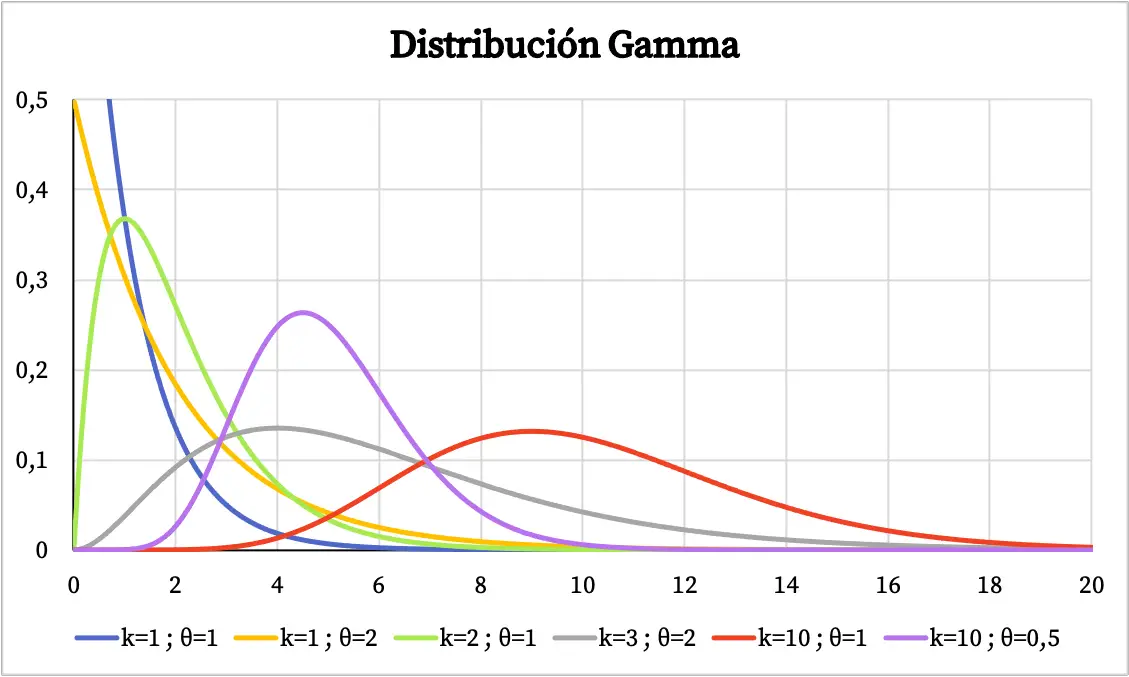
दूसरी ओर, आप गामा वितरण के संचयी संभाव्यता फ़ंक्शन का ग्राफ़ नीचे देख सकते हैं:

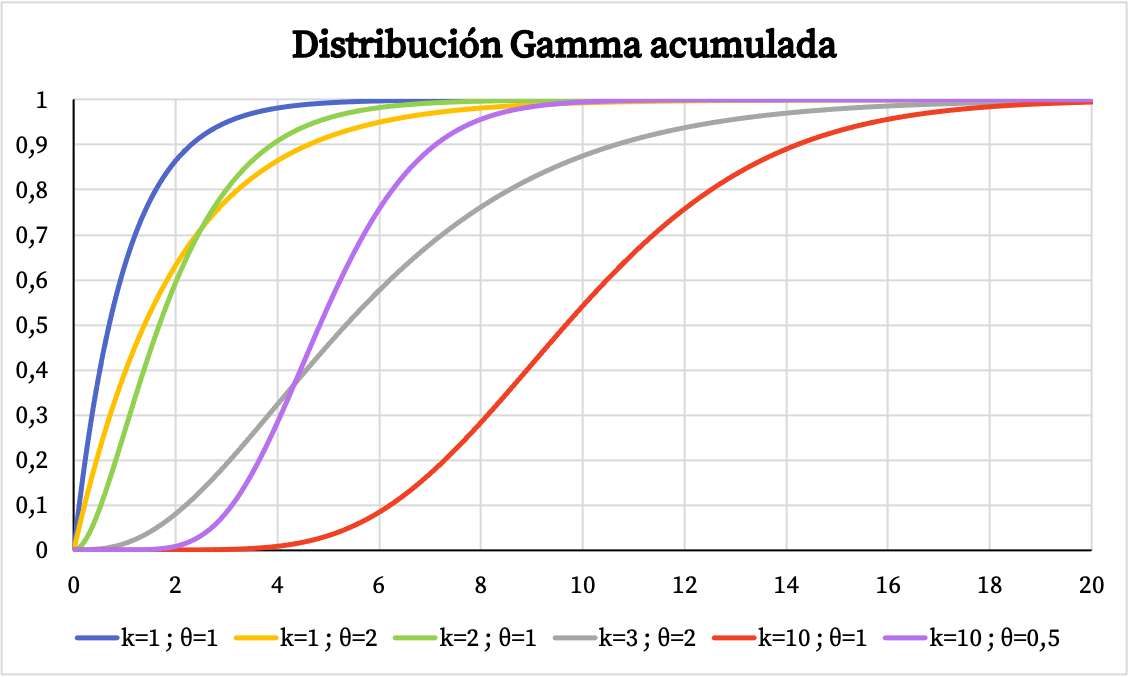
गैम वितरण के संचयी संभाव्यता फ़ंक्शन का ग्राफ़

गामा वितरण के लक्षण

फिर हम देखेंगे कि गामा वितरण की विशेषताएँ क्या हैं।

गामा वितरण का ग्राफ पूरी तरह से इसके दो विशिष्ट मापदंडों द्वारा परिभाषित किया गया है: α आकार पैरामीटर है और λ स्केल पैरामीटर है।

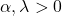
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li> गामा वितरण का क्षेत्र केवल सकारात्मक संख्याओं से बना है।</li> </ul> <p class=$ $x\in (0,+\infty)$

गामा वितरण का माध्य आकार पैरामीटर और स्केल पैरामीटर, यानी α/λ के बीच के अनुपात के बराबर है।

$E[X]=\cfrac{\alpha}{\lambda}$

गामा वितरण का विचरण स्केल पैरामीटर के वर्ग द्वारा विभाजित आकार पैरामीटर के बराबर है।

$Var(X)=\cfrac{\alpha}{\lambda^2}$

1 से कम α के मान के लिए, मोड 0 है। लेकिन यदि α 1 के बराबर या उससे अधिक है, तो गामा वितरण के मोड की गणना निम्न सूत्र से की जा सकती है:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

गामा वितरण के घनत्व फलन का सूत्र है:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

जहां Γ गामा फ़ंक्शन है, जिसे इस प्रकार परिभाषित किया गया है:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

गामा वितरण द्वारा परिभाषित यादृच्छिक चर के संचयी वितरण का सूत्र इस प्रकार है:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

यदि आकार पैरामीटर α 1 के बराबर है, तो गामा वितरण समान स्केल पैरामीटर λ के साथ एक घातीय वितरण के बराबर है।

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

जब स्केल पैरामीटर λ एक औसत है, तो गामा वितरण ची-स्क्वायर वितरण का एक विशेष मामला है।

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

गामा वितरण क्या है?

गामा वितरण आरेख

गामा वितरण के लक्षण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने