Google शीट्स में टी-टेस्ट कैसे करें

सामान्यतया, टी-परीक्षण तीन प्रकार के होते हैं:

• एक नमूना टी परीक्षण
• दो-नमूना टी-परीक्षण
• युग्मित नमूने टी-परीक्षण

यह ट्यूटोरियल Google शीट्स में इनमें से प्रत्येक परीक्षण को निष्पादित करने के उदाहरण प्रदान करता है।

उदाहरण: एक-नमूना टी-परीक्षण

परिभाषा: एक-नमूना टी-परीक्षण का उपयोग यह जांचने के लिए किया जाता है कि किसी जनसंख्या का माध्य एक निश्चित मूल्य के बराबर है या नहीं।

उदाहरण: एक वनस्पतिशास्त्री जानना चाहता है कि क्या एक निश्चित पौधे की प्रजाति की औसत ऊंचाई 15 इंच के बराबर है। वह 12 पौधों का एक यादृच्छिक नमूना लेती है और उनमें से प्रत्येक की ऊंचाई इंच में दर्ज करती है।

निम्नलिखित स्क्रीनशॉट दिखाता है कि यह निर्धारित करने के लिए एक-नमूना टी-परीक्षण कैसे करें कि वास्तविक औसत जनसंख्या ऊंचाई 15 इंच के बराबर है या नहीं:

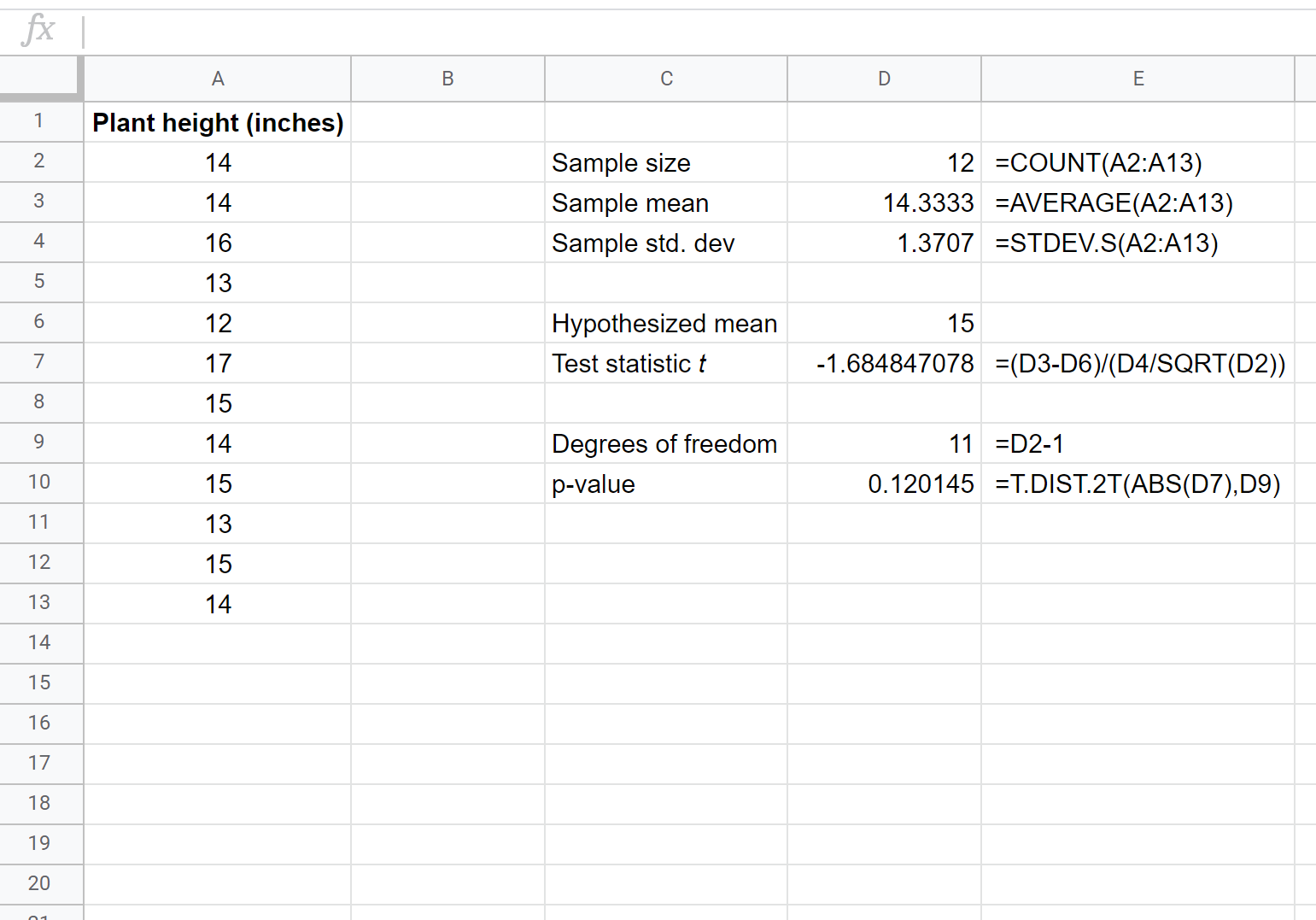
किसी विशेष नमूने पर इस टी-परीक्षण के लिए दो परिकल्पनाएँ इस प्रकार हैं:

एच ₀ : µ = 15 (इस पौधे की प्रजाति की औसत ऊंचाई 15 इंच है)

एच _ए : µ ≠15 (औसत ऊंचाई 15 इंच नहीं है )

हमारे परीक्षण का पी-मान (0.120145) अल्फा = 0.05 से अधिक होने के कारण, हम परीक्षण की शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि इस विशेष प्रजाति के पौधे की औसत ऊंचाई 15 इंच के अलावा कुछ और है।

उदाहरण: दो-नमूना टी-परीक्षण

परिभाषा: दो-नमूना टी-परीक्षण का उपयोग यह जांचने के लिए किया जाता है कि दो आबादी के साधन बराबर हैं या नहीं।

उदाहरण: शोधकर्ता यह जानना चाहते हैं कि क्या किसी देश में दो अलग-अलग पौधों की प्रजातियों की औसत ऊंचाई समान है। वे प्रत्येक प्रजाति से 20 पौधों का एक यादृच्छिक नमूना एकत्र करते हैं और प्रत्येक पौधे की ऊंचाई इंच में दर्ज करते हैं।

निम्नलिखित स्क्रीनशॉट दिखाता है कि दो आबादी की औसत ऊंचाई बराबर है या नहीं यह निर्धारित करने के लिए T.TEST() फ़ंक्शन का उपयोग करके दो-नमूना टी-परीक्षण कैसे करें:

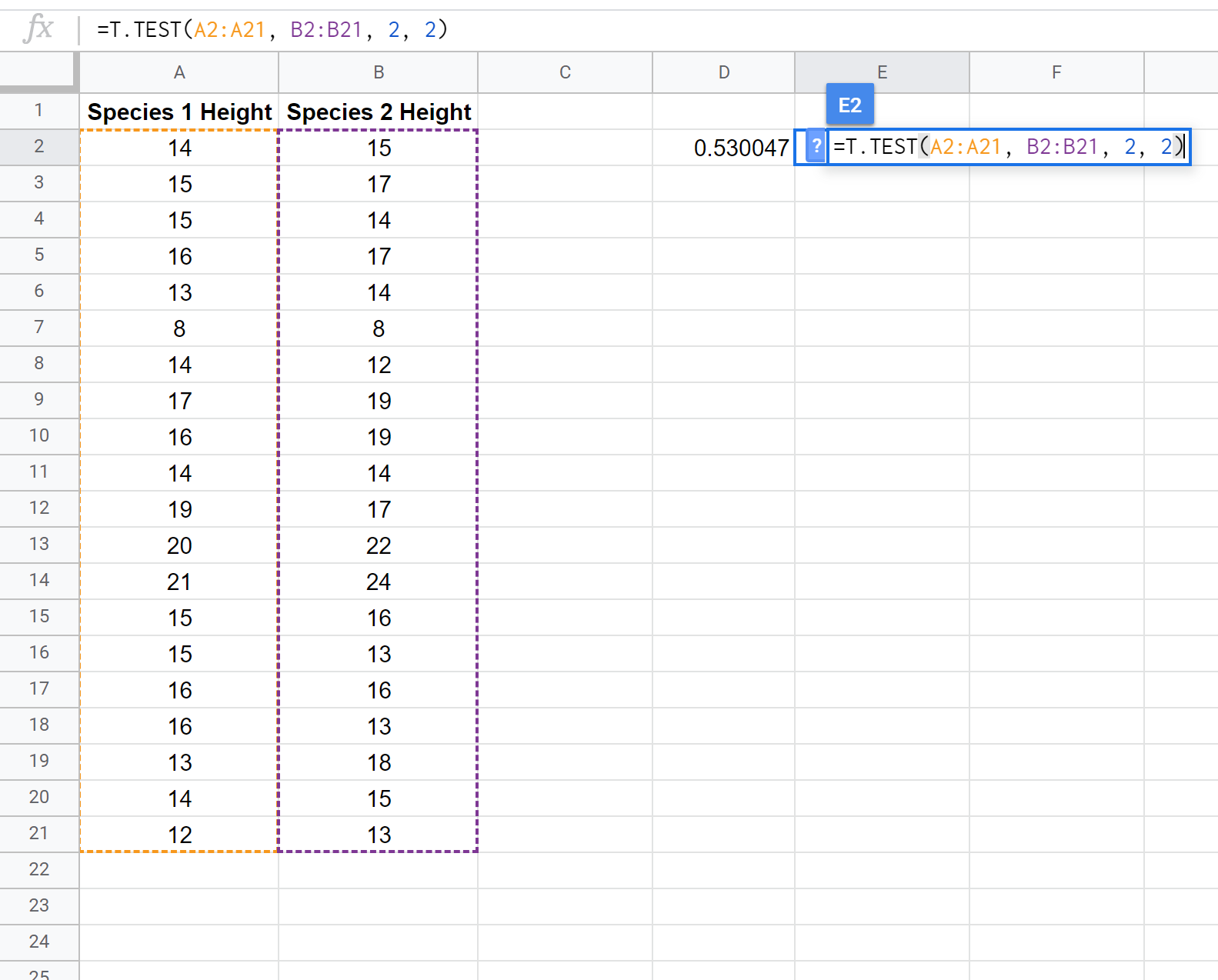
ध्यान दें: इस धारणा के साथ या उसके बिना कि दोनों नमूनों में समान भिन्नता है, एक-पुच्छीय दो-नमूना टी-परीक्षण करना भी संभव है। परीक्षण मान्यताओं को कैसे समायोजित करें यह देखने के लिए T.TEST दस्तावेज़ देखें।

इस दो-नमूना टी-परीक्षण के लिए दो परिकल्पनाएँ हैं:

एच ₀ : μ ₁ = μ ₂ (दोनों जनसंख्या माध्य बराबर हैं)

एच ₁ : μ ₁ ≠ μ ₂ (दोनों जनसंख्या माध्य बराबर नहीं हैं)

क्योंकि हमारे परीक्षण का पी-मान (0.530047) अल्फा = 0.05 से अधिक है, हम परीक्षण की शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि इस विशेष प्रजाति के पौधे की औसत ऊंचाई 15 इंच के अलावा कुछ और है।

उदाहरण: युग्मित नमूने टी-परीक्षण

परिभाषा: एक युग्मित नमूने टी-परीक्षण का उपयोग दो नमूनों के माध्यों की तुलना करने के लिए किया जाता है जब एक नमूने से प्रत्येक अवलोकन को दूसरे नमूने से एक अवलोकन के साथ जोड़ा जा सकता है।

उदाहरण: हम जानना चाहते हैं कि क्या किसी पाठ्यक्रम का किसी विशेष परीक्षा में छात्रों के प्रदर्शन पर महत्वपूर्ण प्रभाव पड़ता है। इसका परीक्षण करने के लिए, हम एक कक्षा में 20 छात्रों को प्री-टेस्ट लेने के लिए कहते हैं। फिर हमने प्रत्येक छात्र को दो सप्ताह के लिए पाठ्यक्रम में भाग लेने के लिए कहा। फिर, छात्र समान कठिनाई की परीक्षा दोबारा देते हैं।

निम्नलिखित स्क्रीनशॉट दिखाता है कि पहले और दूसरे परीक्षण के औसत अंकों के बीच अंतर की तुलना करने के लिए युग्मित नमूना टी-परीक्षण कैसे करें:

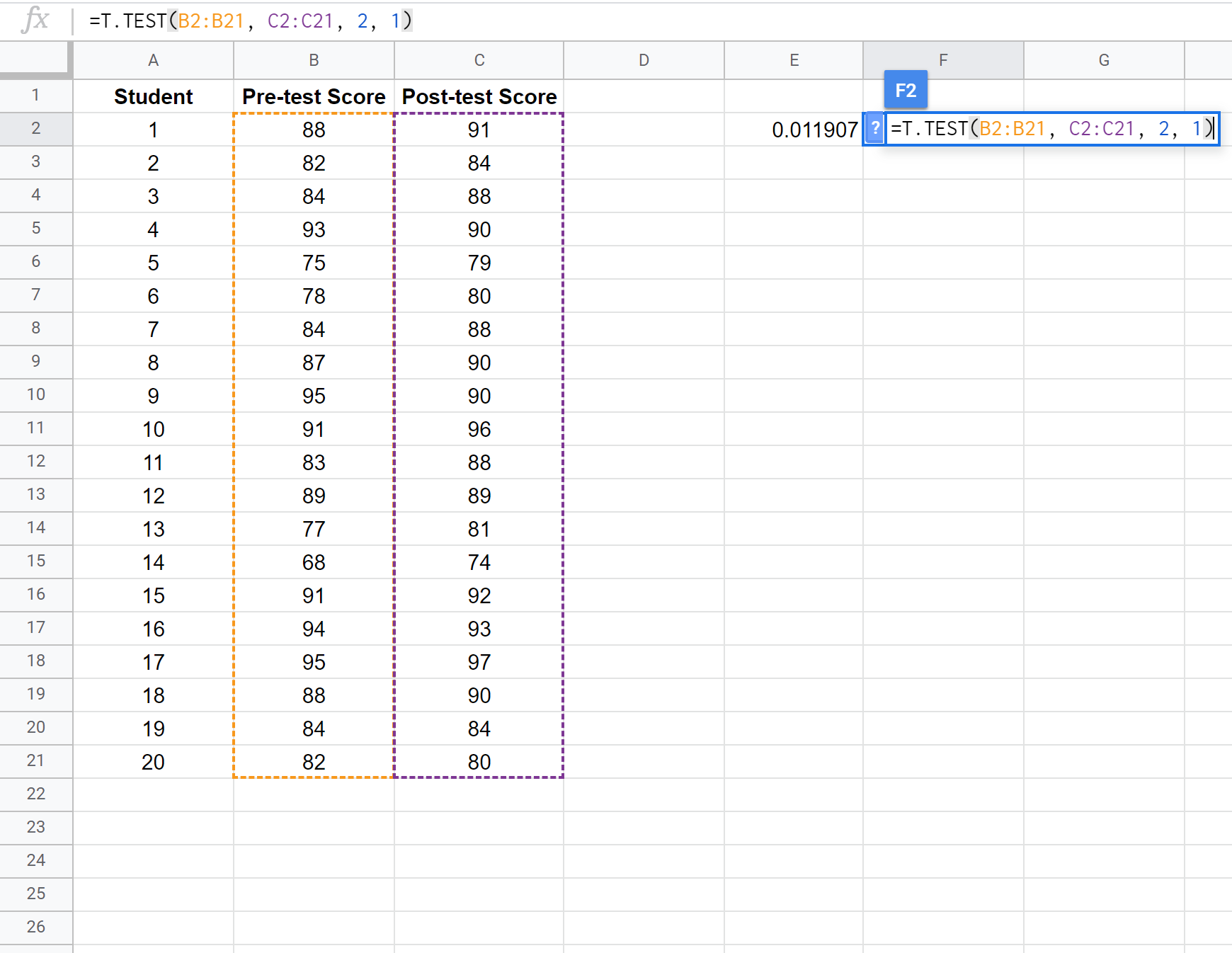
ध्यान दें: इस धारणा के साथ या उसके बिना कि दोनों नमूनों में समान भिन्नता है, एक-पुच्छीय दो-नमूना टी-परीक्षण करना भी संभव है। परीक्षण मान्यताओं को कैसे समायोजित करें यह देखने के लिए T.TEST दस्तावेज़ देखें।

इस युग्मित नमूने टी-परीक्षण के लिए दो धारणाएँ हैं:

एच ₀ : μ ₁ = μ ₂ (दोनों जनसंख्या माध्य बराबर हैं)

एच ₁ : μ ₁ ≠ μ ₂ (दोनों जनसंख्या माध्य बराबर नहीं हैं)

चूँकि हमारे परीक्षण का पी-मान (0.011907) अल्फा = 0.05 से कम है, हम परीक्षण की शून्य परिकल्पना को अस्वीकार करते हैं। हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि प्री-टेस्ट और पोस्ट-टेस्ट माध्य स्कोर के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है।