घातांकी रूप से वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में घातीय वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसी तरह, आप पाएंगे कि घातीय वितरण के गुण क्या हैं, साथ ही इसके सूत्र, इसका ग्राफ और एक हल किया गया अभ्यास भी। इसके अतिरिक्त, आप ऑनलाइन घातीय वितरण कैलकुलेटर के साथ किसी भी संभावना की गणना करने में सक्षम होंगे।

घातीय वितरण क्या है?

घातीय वितरण एक सतत संभाव्यता वितरण है जिसका उपयोग किसी यादृच्छिक घटना के घटित होने के प्रतीक्षा समय को मॉडल करने के लिए किया जाता है।

अधिक सटीक रूप से, घातीय वितरण हमें पॉइसन वितरण के बाद होने वाली दो घटनाओं के बीच प्रतीक्षा समय का वर्णन करने की अनुमति देता है। इसलिए, घातीय वितरण पॉइसन वितरण से निकटता से संबंधित है।

➤ देखें: पॉइसन वितरण क्या है?

घातीय वितरण में एक विशिष्ट पैरामीटर होता है, जिसे ग्रीक अक्षर λ द्वारा दर्शाया जाता है और यह इंगित करता है कि किसी निश्चित अवधि के दौरान अध्ययन की गई घटना कितनी बार घटित होने की उम्मीद है।

$X\sim \text{Exp}(\lambda)$

इसी प्रकार, घातीय वितरण का उपयोग विफलता होने तक के समय को मॉडल करने के लिए भी किया जाता है। इसलिए घातांकीय वितरण की विश्वसनीयता और उत्तरजीविता सिद्धांत में कई अनुप्रयोग हैं।

घातीय वितरण के उदाहरण

अब जब हम घातीय वितरण की परिभाषा जानते हैं, तो आइए अवधारणा को बेहतर ढंग से समझने के लिए इस प्रकार के वितरण के कई उदाहरण देखें।

घातीय वितरण के उदाहरण:

एक कॉल सेंटर में दो कॉलों के बीच बीता हुआ समय.
वह समय जब किसी व्यक्ति को किसी विशिष्ट सड़क पर निःशुल्क टैक्सी गुजरने तक प्रतीक्षा करनी पड़ती है।
किसी नए ग्राहक के स्टोर में प्रवेश करने तक का प्रतीक्षा समय।
किसी वेब पेज में प्रवेश करने वाले दो अलग-अलग उपयोगकर्ताओं के बीच का समय।
एक हवाई अड्डे पर एक विमान के उड़ान भरने और दूसरे के प्रस्थान के बीच का समय समाप्त हो गया।

घातीय वितरण सूत्र

घनत्व फ़ंक्शन सूत्र जो एक घातांकीय वितरण संभावना की गणना को परिभाषित करता है, वह λ को संख्या e से गुणा करके ऋणात्मक λ गुणा x की घात के बराबर होता है।

दूसरे शब्दों में, घातीय वितरण संभावना की गणना करने का सूत्र इस प्रकार है:

👉 आप घातीय वितरण का अनुसरण करने वाले एक चर की संभावना की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

दूसरी ओर, घातीय वितरण की संचयी संभावना की गणना करने का सूत्र इस प्रकार है:

$P[X\leq x]=1-e^{-\lambda x}$

घातांकीय वितरण ग्राफ

इस अनुभाग में आप घनत्व फ़ंक्शन और घातीय वितरण के वितरण फ़ंक्शन का ग्राफिकल प्रतिनिधित्व देख सकते हैं।

नीचे आप देख सकते हैं कि घातीय वितरण के घनत्व फ़ंक्शन का ग्राफ़ पैरामीटर λ के मान के आधार पर कैसे भिन्न होता है।

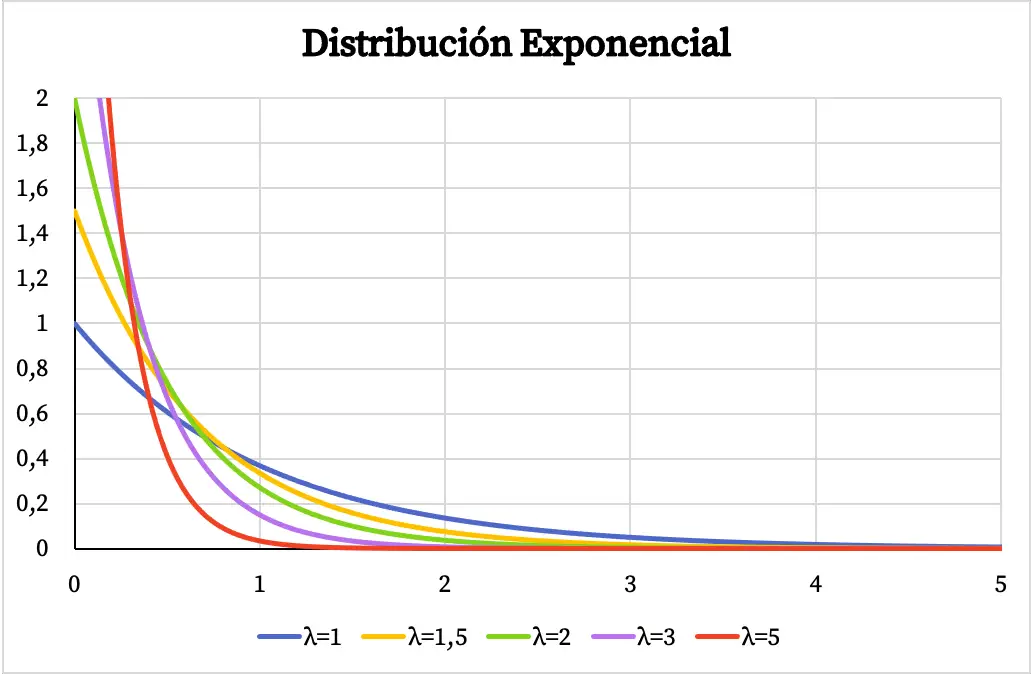
इसी तरह, घातीय वितरण का संचयी संभाव्यता फ़ंक्शन भी पैरामीटर λ के मान पर निर्भर करता है, जैसा कि आप निम्नलिखित ग्राफ़ में देख सकते हैं:

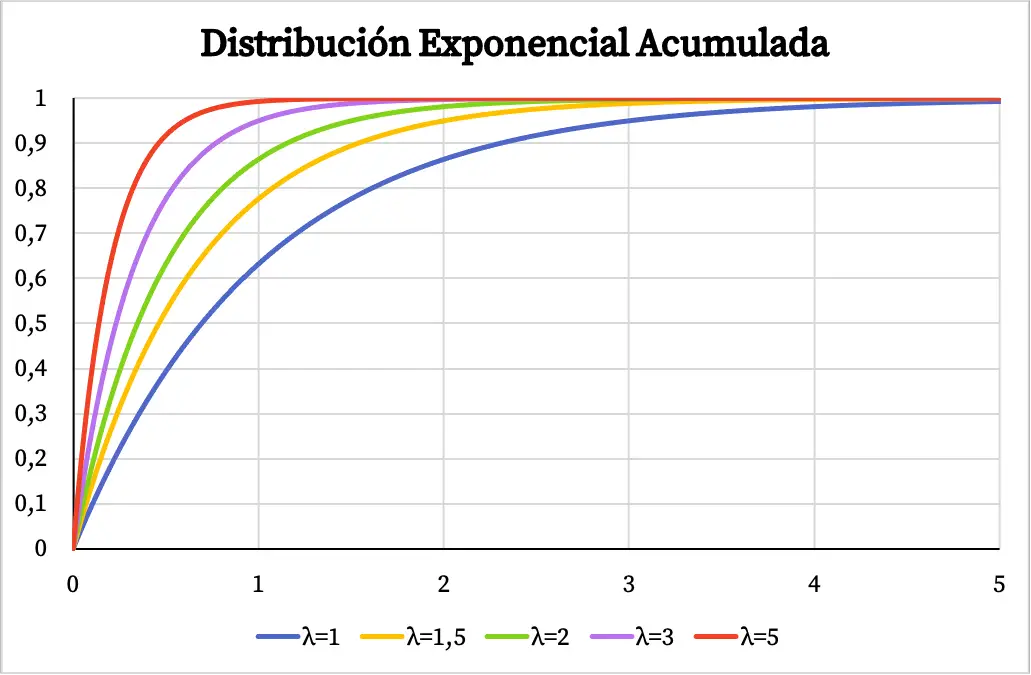
घातीय वितरण पर हल किया गया अभ्यास

औसतन, λ=1 उपयोगकर्ता/मिनट एक विशिष्ट वेब पेज तक पहुंचते हैं। इसकी क्या प्रायिकता है कि दो उपयोगकर्ताओं के प्रवेश के बीच का समय 3 मिनट है? और इसकी प्रायिकता कि यह 2 मिनट के बराबर या उससे कम है?

वितरण जो इस समस्या के यादृच्छिक चर को परिभाषित करता है वह एक घातीय वितरण है, क्योंकि हम उस समय का अध्ययन करते हैं जो किसी घटना के घटित होने के क्षण (वेब पेज पर उपयोगकर्ता की प्रविष्टि) से लेकर उसी घटना के दोबारा घटित होने तक बीतता है।

$X\sim \text{Exp}(1)$

इसलिए, इस संभावना की गणना करने के लिए कि दो अलग-अलग उपयोगकर्ताओं के प्रवेश के बीच का समय तीन मिनट है, हमें घनत्व फ़ंक्शन सूत्र लागू करने की आवश्यकता है (ऊपर देखें):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

दूसरी ओर, संचयी संभाव्यता निर्धारित करने के लिए, हमें घातीय वितरण के वितरण फ़ंक्शन सूत्र का उपयोग करना चाहिए:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

घातीय वितरण के लक्षण

घातीय वितरण में निम्नलिखित विशेषताएं हैं:

घातीय वितरण में एक विशिष्ट पैरामीटर, λ होता है, जो इंगित करता है कि किसी निश्चित अवधि के दौरान अध्ययन की गई घटना कितनी बार घटित होने की उम्मीद है।

$X\sim \text{Exp}(\lambda)$

घातांकीय वितरण ऋणात्मक मान नहीं ले सकता, इसलिए घातांकीय वितरण के क्षेत्र में शून्य से अधिक या उसके बराबर सभी वास्तविक संख्याएँ शामिल होती हैं।

$x\in [0,+\infty)$

घातीय वितरण का माध्य विशेषता पैरामीटर λ द्वारा विभाजित एक के बराबर है।

$E[X]=\cfrac{1}{\lambda}$

घातांकीय वितरण का प्रसरण इसके माध्य का वर्ग है, इसलिए घातांकीय वितरण का प्रसरण गुणांक λ वर्ग के एक के बराबर है।

$Var(X)=\cfrac{1}{\lambda^2 }$

λ का मान जो भी हो, घातीय वितरण का असममिति गुणांक हमेशा 2 के बराबर होता है।

$A=2$

इसी प्रकार, किसी भी घातीय वितरण का कर्टोसिस गुणांक हमेशा 9 के बराबर होता है।

$C=9$

घातांकीय वितरण के घनत्व फलन का सूत्र है:

$P[X=x]=\lambda e^{-\lambda x}$

जबकि घातीय वितरण के संचयी संभाव्यता फ़ंक्शन का सूत्र इस प्रकार है:

$P[X\leq x]=1-e^{-\lambda x}$

घातीय वितरण आउट-ऑफ़-मेमोरी संपत्ति वाले कुछ संभाव्यता वितरणों में से एक है। इस गुण का अर्थ है कि पिछली घटना के घटित होने से भविष्य में उस घटना के घटित होने की संभावना प्रभावित नहीं होती है। उदाहरण के लिए, एक घातीय वितरण में, एक नए उपयोगकर्ता द्वारा एक मिनट से भी कम समय में वेब पेज तक पहुंचने की संभावना इस बात पर निर्भर नहीं करती है कि उपयोगकर्ता ने अभी प्रवेश किया है या उसके बाद से किसी उपयोगकर्ता ने प्रवेश नहीं किया है। दस मिनट से अधिक.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ घातीय वितरण कैलकुलेटर

संभाव्यता की गणना करने के लिए निम्नलिखित कैलकुलेटर में पैरामीटर λ का मान और x का मान दर्ज करें। आपको उस संभावना का चयन करना होगा जिसकी आप गणना करना चाहते हैं और दशमलव विभाजक के रूप में बिंदु का उपयोग करके संख्याएं दर्ज करें, उदाहरण के लिए 0.50।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने