घुमावदार अवशिष्ट कथानक की व्याख्या कैसे करें (उदाहरण के साथ)

अवशिष्ट भूखंडों का उपयोग यह आकलन करने के लिए किया जाता है कि क्या प्रतिगमन मॉडल के अवशेष सामान्य रूप से वितरित किए जाते हैं और क्या वे विषमलैंगिकता प्रदर्शित करते हैं या नहीं।

आदर्श रूप से, आप चाहेंगे कि अवशिष्ट प्लॉट में बिंदु बिना किसी स्पष्ट पैटर्न के, शून्य के मान के आसपास बेतरतीब ढंग से बिखरे हुए हों।

यदि आपको एक अवशिष्ट प्लॉट मिलता है जिसमें प्लॉट बिंदुओं पर एक घुमावदार पैटर्न होता है, तो संभवतः इसका मतलब है कि डेटा के लिए आपके द्वारा निर्दिष्ट प्रतिगमन मॉडल सही नहीं है।

ज्यादातर मामलों में, इसका मतलब यह है कि आपने एक रैखिक प्रतिगमन मॉडल को एक डेटा सेट में फिट करने का प्रयास किया है जो इसके बजाय एक द्विघात प्रवृत्ति का अनुसरण करता है।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में घुमावदार अवशिष्ट कथानक की व्याख्या (और सही) कैसे की जाए।

उदाहरण: एक घुमावदार अवशिष्ट कथानक की व्याख्या करना

मान लीजिए कि हम एक कार्यालय में 11 अलग-अलग लोगों के लिए प्रति सप्ताह काम किए गए घंटों की संख्या और खुशी के रिपोर्ट किए गए स्तर (0 से 100 के पैमाने पर) पर निम्नलिखित डेटा एकत्र करते हैं:

यदि हमने खुशी के स्तर बनाम काम किए गए घंटों का एक सरल स्कैटरप्लॉट बनाया, तो यह इस तरह दिखेगा:

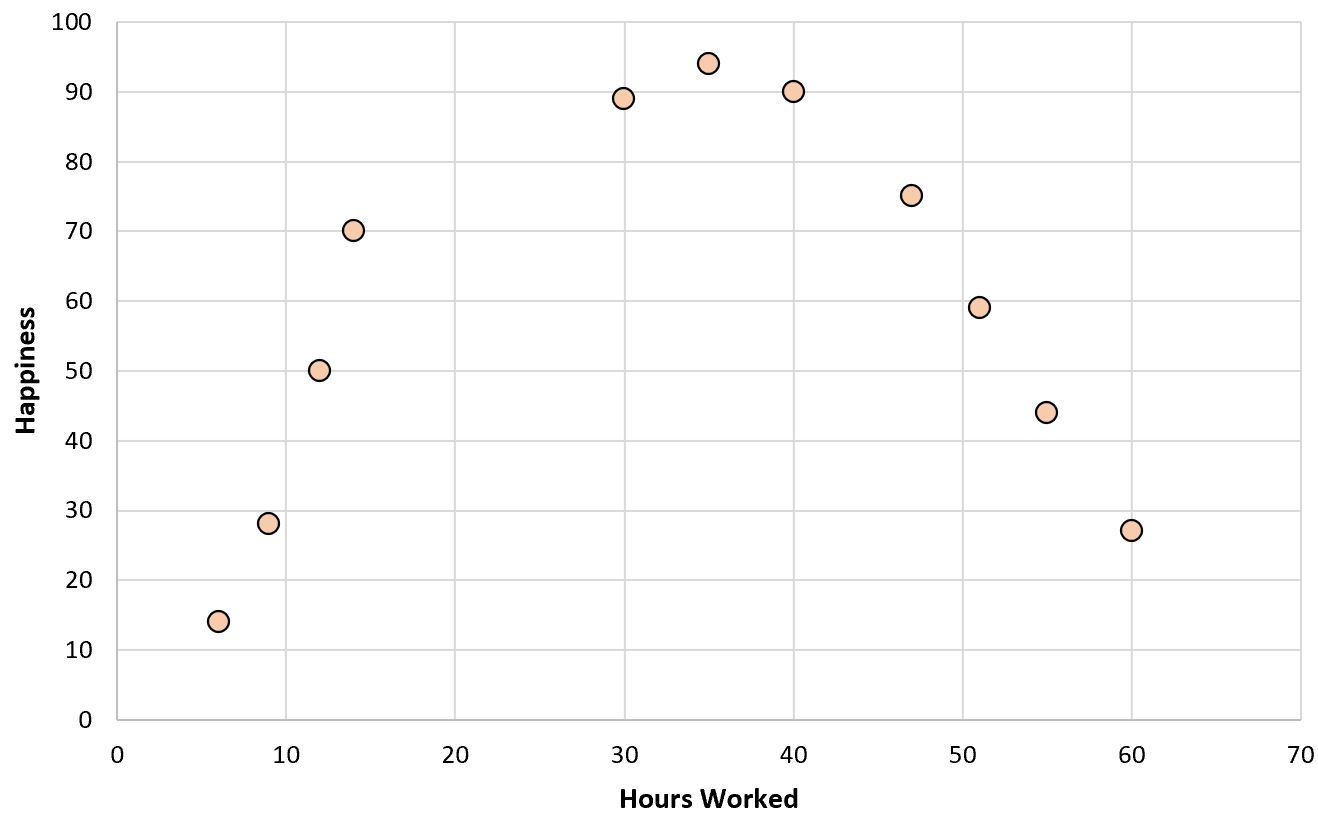
अब मान लीजिए कि हम खुशी के स्तर की भविष्यवाणी करने के लिए काम किए गए घंटों का उपयोग करके एक प्रतिगमन मॉडल फिट करना चाहते हैं।

निम्नलिखित कोड दिखाता है कि इस डेटासेट में एक सरल रैखिक प्रतिगमन मॉडल को कैसे फिट किया जाए और आर में एक अवशिष्ट प्लॉट तैयार किया जाए:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

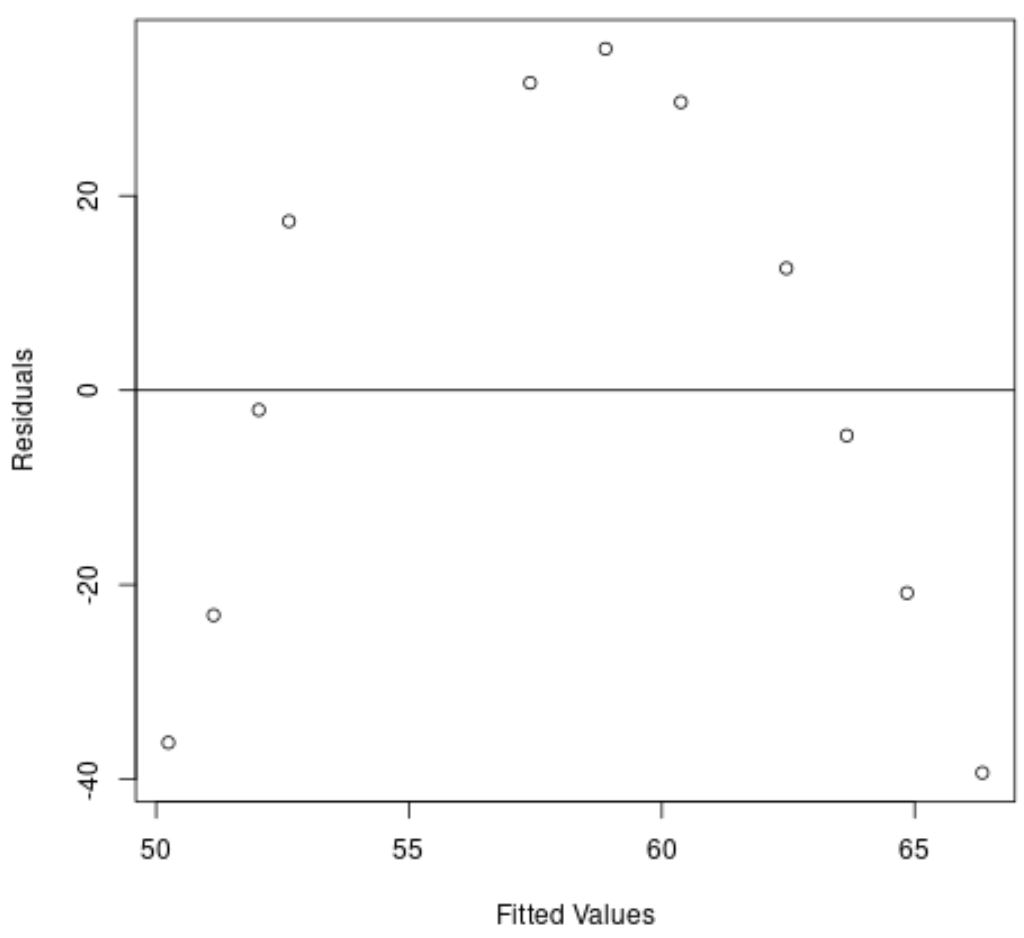
x-अक्ष फिट किए गए मान प्रदर्शित करता है और y-अक्ष अवशिष्ट प्रदर्शित करता है।

ग्राफ़ से, हम देख सकते हैं कि अवशेषों में एक घुमावदार पैटर्न है, जो दर्शाता है कि एक रैखिक प्रतिगमन मॉडल इस डेटा सेट के लिए उपयुक्त फिट प्रदान नहीं करता है।

निम्नलिखित कोड दिखाता है कि इस डेटा सेट में एक द्विघात प्रतिगमन मॉडल को कैसे फिट किया जाए और आर में एक अवशिष्ट प्लॉट तैयार किया जाए:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

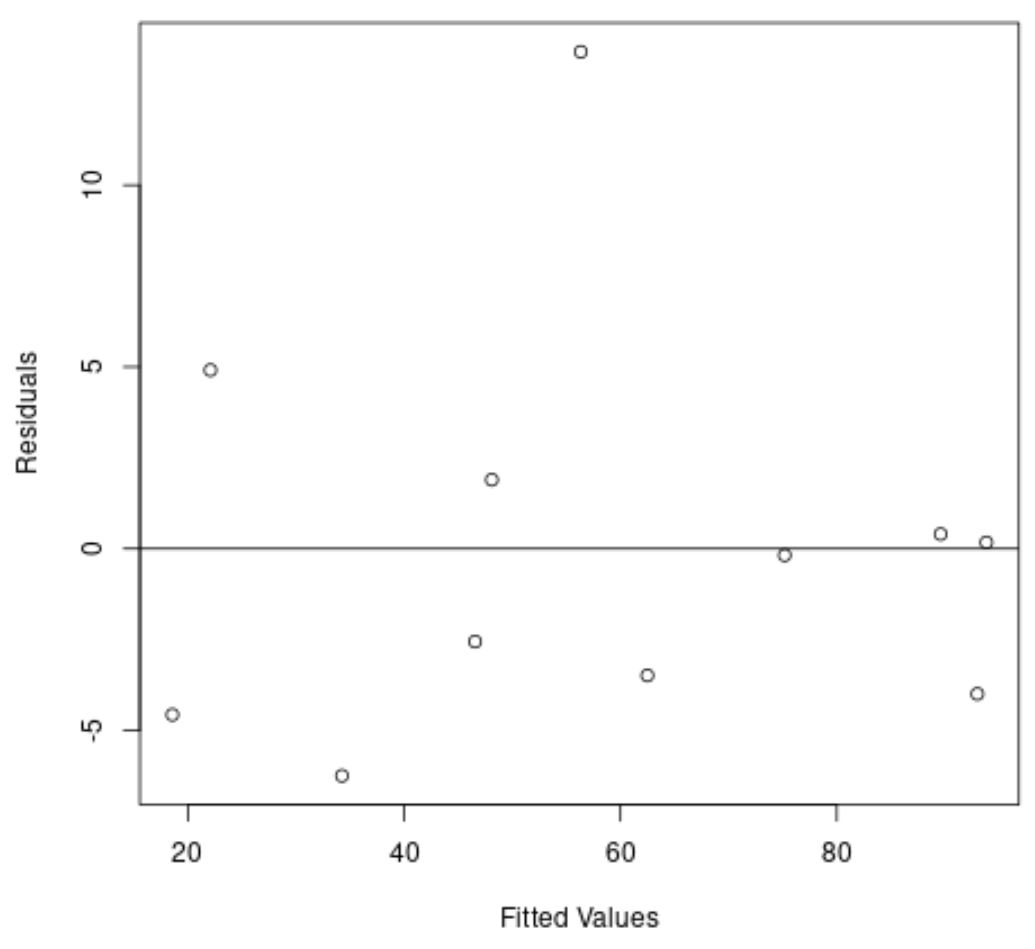
एक बार फिर, x-अक्ष फिट किए गए मान दिखाता है और y-अक्ष अवशिष्ट दिखाता है।

कथानक से हम देख सकते हैं कि अवशेष शून्य के आसपास बेतरतीब ढंग से बिखरे हुए हैं और अवशेषों में कोई स्पष्ट प्रवृत्ति नहीं है।

यह हमें बताता है कि एक द्विघात प्रतिगमन मॉडल एक रैखिक प्रतिगमन मॉडल की तुलना में इस डेटा सेट को फिट करने का बेहतर काम करता है।

इसका मतलब यह होना चाहिए कि हमने देखा कि काम के घंटे और खुशी के स्तर के बीच वास्तविक संबंध रैखिक के बजाय द्विघात प्रतीत होता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके अवशिष्ट प्लॉट कैसे बनाएं:

हाथ से एक अवशिष्ट पथ कैसे बनाएं
आर में अवशिष्ट प्लॉट कैसे बनाएं
एक्सेल में एक अवशिष्ट प्लॉट कैसे बनाएं
पायथन में एक अवशिष्ट प्लॉट कैसे बनाएं