एसएएस में आरओसी कर्व कैसे बनाएं

लॉजिस्टिक रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम रिग्रेशन मॉडल को फिट करने के लिए कर सकते हैं जब प्रतिक्रिया चर द्विआधारी होता है।

यह मूल्यांकन करने के लिए कि लॉजिस्टिक रिग्रेशन मॉडल डेटा सेट में कितनी अच्छी तरह फिट बैठता है, हम निम्नलिखित दो मैट्रिक्स देख सकते हैं:

• संवेदनशीलता: संभावना है कि मॉडल किसी अवलोकन के लिए सकारात्मक परिणाम की भविष्यवाणी करता है जब परिणाम वास्तव में सकारात्मक होता है। इसे “सच्ची सकारात्मक दर” भी कहा जाता है।
• विशिष्टता: संभावना है कि मॉडल किसी अवलोकन के लिए नकारात्मक परिणाम की भविष्यवाणी करता है जब परिणाम वास्तव में नकारात्मक होता है। इसे “सच्ची नकारात्मक दर” भी कहा जाता है।

इन दो मापों को देखने का एक तरीका एक आरओसी वक्र बनाना है, जो “रिसीवर ऑपरेटिंग विशेषता” वक्र के लिए है। यह एक ग्राफ़ है जो लॉजिस्टिक रिग्रेशन मॉडल की संवेदनशीलता और विशिष्टता को प्रदर्शित करता है।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि एसएएस में आरओसी वक्र कैसे बनाएं और व्याख्या करें।

चरण 1: डेटासेट बनाएं

सबसे पहले, हम 18 छात्रों के लिए निम्नलिखित चर पर जानकारी युक्त एक डेटासेट बनाएंगे:

• एक निश्चित कॉलेज में स्वीकृति (1 = हाँ, 0 = नहीं)
• जीपीए (1 से 4 का पैमाना)
• ACT स्कोर (1 से 36 का पैमाना)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

चरण 2: लॉजिस्टिक रिग्रेशन मॉडल को फिट करें और एक आरओसी वक्र बनाएं

इसके बाद, हम लॉजिस्टिक रिग्रेशन मॉडल को फिट करने के लिए प्रोक लॉजिस्टिक्स का उपयोग करेंगे, प्रतिक्रिया चर के रूप में “स्वीकृति” और भविष्यवक्ता चर के रूप में “जीपीए” और “एक्ट” का उपयोग करेंगे।

हम घटते हुए को निर्दिष्ट करेंगे ताकि एसएएस को पता चले कि इस संभावना की भविष्यवाणी कैसे की जाए कि प्रतिक्रिया चर मान 1 लेता है।

हम मॉडल के लिए आरओसी वक्र बनाने के लिए प्लॉट्स (केवल) = रॉक का भी उपयोग करेंगे:

 /*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
  model acceptance = gpa act;
run ;

चरण 3: आरओसी वक्र की व्याख्या करें

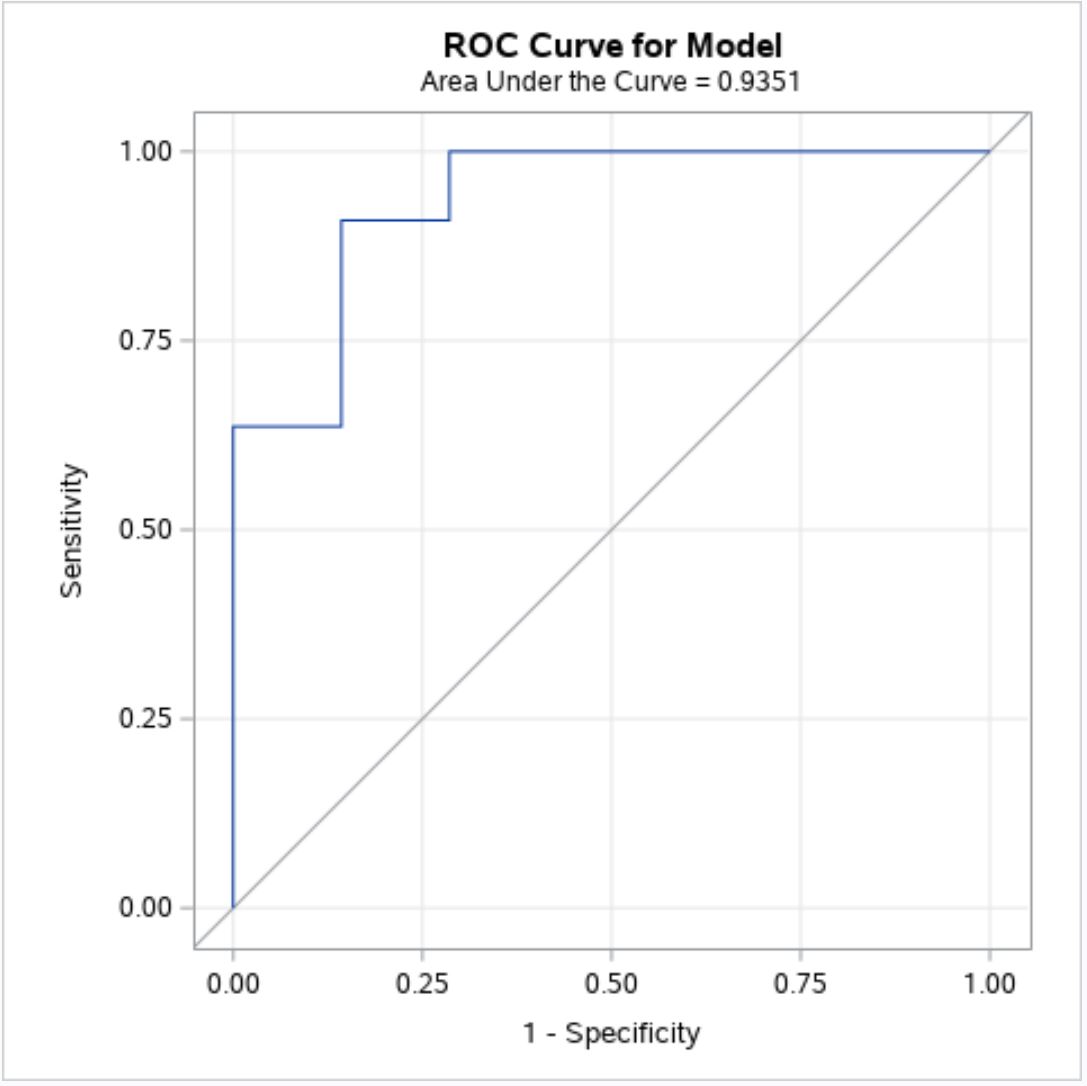
आरओसी वक्र प्लॉट के ऊपरी बाएँ कोने के जितना करीब फिट होता है, मॉडल उतना ही बेहतर डेटा सेट में प्रतिक्रिया मूल्यों के मूल्य की भविष्यवाणी करता है।

ऊपर दिए गए ग्राफ़ से, हम देख सकते हैं कि नीला आरओसी वक्र ऊपरी बाएँ कोने को घेरता है, यह दर्शाता है कि लॉजिस्टिक रिग्रेशन मॉडल प्रतिक्रिया मूल्यों के मूल्य की भविष्यवाणी करने का अच्छा काम कर रहा है।

यह निर्धारित करने के लिए कि लॉजिस्टिक रिग्रेशन मॉडल डेटा में कितनी अच्छी तरह फिट बैठता है, हम एयूसी – वक्र के नीचे का क्षेत्र – की गणना कर सकते हैं – जो हमें बताता है कि प्लॉट का कितना हिस्सा वक्र के नीचे है।

AUC 1 के जितना करीब होगा, मॉडल उतना ही बेहतर होगा। 0.5 के बराबर एयूसी वाला मॉडल यादृच्छिक वर्गीकरण करने वाले मॉडल से बेहतर नहीं है।

उपरोक्त चार्ट शीर्षक के तहत, हम देख सकते हैं कि इस मॉडल का AUC 0.9351 है।

चूँकि यह मान एक के करीब है, यह पुष्टि करता है कि मॉडल प्रतिक्रिया मूल्यों के मूल्य की अच्छी तरह से भविष्यवाणी करता है।

हम विभिन्न लॉजिस्टिक रिग्रेशन मॉडल के फिट की तुलना करने के लिए एयूसी मान का भी उपयोग कर सकते हैं।

उदाहरण के लिए, मान लीजिए कि हम दो अलग-अलग लॉजिस्टिक रिग्रेशन मॉडल फिट करते हैं और प्रत्येक के लिए एयूसी मूल्यों की गणना करते हैं:

• मॉडल 1 का एयूसी: 0.9351
• मॉडल 2 का एयूसी: 0.8140

चूँकि मॉडल 1 का AUC बड़ा है, यह हमें बताता है कि मॉडल 1 मॉडल 2 की तुलना में डेटा को फिट करने का बेहतर काम करता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य सामान्य ऑपरेशन कैसे करें:

एसएएस में सरल रैखिक प्रतिगमन कैसे करें
एसएएस में मल्टीपल लीनियर रिग्रेशन कैसे करें
एसएएस में लॉजिस्टिक रिग्रेशन कैसे करें