एसएएस में चरणबद्ध प्रतिगमन कैसे करें (उदाहरण के साथ)

चरणबद्ध प्रतिगमन एक ऐसी प्रक्रिया है जिसका उपयोग हम मॉडल में चरण-दर-चरण तरीके से भविष्यवक्ताओं को दर्ज करने और हटाने के द्वारा भविष्यवक्ता चर के एक सेट से एक प्रतिगमन मॉडल बनाने के लिए कर सकते हैं जब तक कि इसमें प्रवेश करने या करने के लिए कोई सांख्यिकीय रूप से मान्य कारण न हो। अधिक हटाएं.

चरणबद्ध प्रतिगमन का लक्ष्य एक प्रतिगमन मॉडल बनाना है जिसमें सभी भविष्यवक्ता चर शामिल हैं जो सांख्यिकीय रूप से प्रतिक्रिया चर से महत्वपूर्ण रूप से संबंधित हैं।

एसएएस में चरणबद्ध प्रतिगमन करने के लिए, आप चयन कथन के साथ PROC REG का उपयोग कर सकते हैं।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में एसएएस में चरणबद्ध प्रतिगमन कैसे करें।

उदाहरण: एसएएस में चरण-दर-चरण प्रतिगमन करना

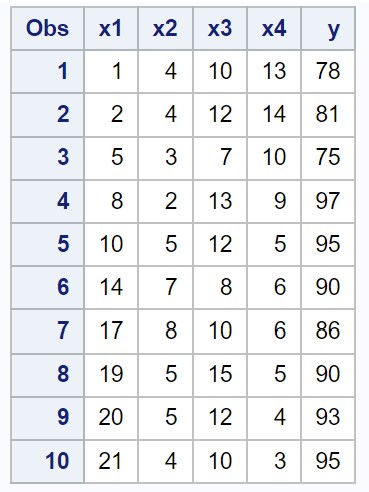
मान लीजिए कि हमारे पास एसएएस में निम्नलिखित डेटासेट है जिसमें चार भविष्यवक्ता चर (x1, x2, x3, x4) और एक प्रतिक्रिया चर (y) शामिल हैं:

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

अब मान लीजिए कि हम यह निर्धारित करना चाहते हैं कि भविष्यवक्ता चर का कौन सा संयोजन सर्वोत्तम एकाधिक रैखिक प्रतिगमन मॉडल का उत्पादन करेगा।

जब हम “सर्वोत्तम” प्रतिगमन मॉडल के बारे में बात करते हैं, तो हमारा मतलब उस मॉडल से है जो कुछ उपायों को अधिकतम या न्यूनतम करता है।

संभावित मॉडलों के समूह में कौन सा प्रतिगमन मॉडल सबसे अच्छा है, इसका मूल्यांकन करने के लिए हम आमतौर पर दो मैट्रिक्स का उपयोग करते हैं:

1. समायोजित आर-वर्ग : समायोजित आर-वर्ग मान हमें एक मॉडल की उपयोगिता बताता है, जिसे एक मॉडल में भविष्यवक्ताओं की संख्या के आधार पर समायोजित किया जाता है। उच्चतम समायोजित आर-वर्ग मान वाला मॉडल सबसे अच्छा माना जाता है।

2. एआईसी : अकाइक सूचना मानदंड (एआईसी) एक मीट्रिक है जिसका उपयोग विभिन्न प्रतिगमन मॉडल के फिट की तुलना करने के लिए किया जाता है। सबसे कम AIC वैल्यू वाला मॉडल सबसे अच्छा माना जाता है।

सौभाग्य से, हम चयन कथन के साथ PROC REG का उपयोग करके एसएएस में प्रतिगमन मॉडल के लिए फिट किए गए आर-स्क्वायर और एआईसी दोनों मूल्यों की गणना कर सकते हैं।

निम्नलिखित कोड दिखाता है कि यह कैसे करना है:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

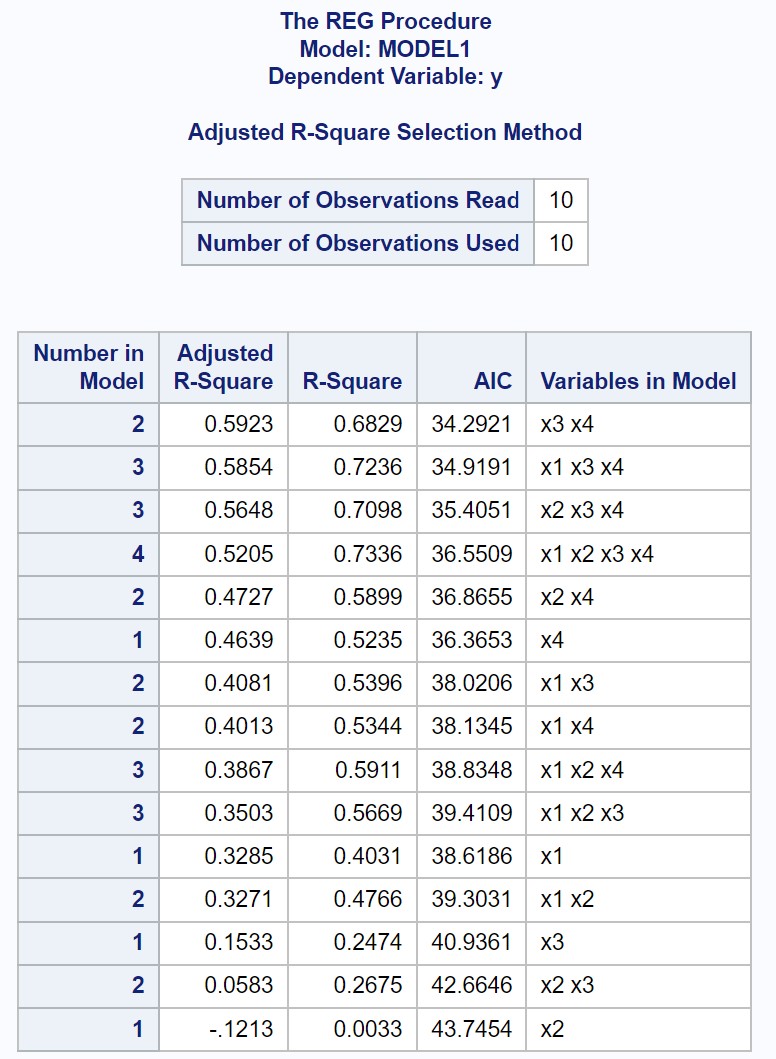
आउटपुट प्रत्येक संभावित एकाधिक रैखिक प्रतिगमन मॉडल के लिए फिट किए गए आर-स्क्वायर और एआईसी मान प्रदर्शित करता है।

परिणाम से, हम देख सकते हैं कि उच्चतम समायोजित आर वर्ग मान और न्यूनतम एआईसी मान वाला मान प्रतिगमन मॉडल है जो केवल x3 और x4 को भविष्यवक्ता चर के रूप में उपयोग करता है।

इस प्रकार, हम घोषणा करते हैं कि निम्नलिखित मॉडल सभी संभावित मॉडलों में “सर्वश्रेष्ठ” है:

y = b ₀ + b ₁ (x3) + b ₂ (x4)

इस विशेष प्रतिगमन मॉडल में निम्नलिखित मैट्रिक्स हैं:

• समायोजित आर-वर्ग मान: 0.5923
• एआईसी: 34.2921

“सर्वोत्तम” प्रतिगमन मॉडल के चयन पर नोट्स

ध्यान दें कि कभी-कभी उच्चतम समायोजित आर-वर्ग मान वाले मॉडल में हमेशा सबसे कम एआईसी मान नहीं होता है।

जब यह तय करने की बात आती है कि कौन सा प्रतिगमन मॉडल सबसे अच्छा है, तो समायोजित आर-स्क्वायर और एआईसी सुझाव के रूप में काम करते हैं, लेकिन वास्तविक दुनिया में आपको यह निर्धारित करने के लिए डोमेन विशेषज्ञता का उपयोग करने की आवश्यकता हो सकती है कि कौन सा मॉडल सबसे अच्छा है।

एक मितव्ययी मॉडल चुनना भी बुद्धिमानी हो सकता है, अर्थात, एक ऐसा मॉडल जो यथासंभव कम भविष्यवक्ता चर का उपयोग करके वांछित स्तर को प्राप्त करता है।

इस प्रकार के मॉडल के पीछे का तर्क ओकाम के रेजर (कभी-कभी “पारसीमोनी सिद्धांत” कहा जाता है) के विचार से उत्पन्न होता है जो कहता है कि सबसे सरल स्पष्टीकरण संभवतः सही है।

आँकड़ों पर लागू करें, एक मॉडल जिसमें कुछ पैरामीटर हैं लेकिन फिट का एक संतोषजनक स्तर प्राप्त होता है उसे उस मॉडल की तुलना में प्राथमिकता दी जानी चाहिए जिसमें बहुत सारे पैरामीटर हैं और केवल थोड़ा उच्च स्तर का फिट प्राप्त होता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य सामान्य कार्य कैसे करें:

एसएएस में सरल रैखिक प्रतिगमन कैसे करें
एसएएस में मल्टीपल लीनियर रिग्रेशन कैसे करें
एसएएस में बहुपद प्रतिगमन कैसे करें
एसएएस में लॉजिस्टिक रिग्रेशन कैसे करें