ची-स्क्वायर वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 4, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि ची-स्क्वायर वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसके अतिरिक्त, आपको ची-स्क्वायर वितरण ग्राफ़ और उसके गुण मिलेंगे।

ची-स्क्वायर वितरण क्या है?

ची-स्क्वायर वितरण एक संभाव्यता वितरण है जिसका प्रतीक χ² है। अधिक सटीक रूप से, ची-स्क्वायर वितरण सामान्य वितरण के साथ k स्वतंत्र यादृच्छिक चर के वर्ग का योग है।

इस प्रकार, ची-स्क्वायर वितरण में स्वतंत्रता की k डिग्री है। इसलिए, एक ची-स्क्वायर वितरण में स्वतंत्रता की उतनी ही डिग्री होती है जितनी सामान्य रूप से वितरित चर के वर्गों का योग इसका प्रतिनिधित्व करता है।

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

ची-स्क्वायर वितरण को पियर्सन वितरण के रूप में भी जाना जाता है।

यह ध्यान दिया जाना चाहिए कि ची-स्क्वायर वितरण गामा वितरण का एक विशेष मामला है।

ची-स्क्वायर वितरण का व्यापक रूप से सांख्यिकीय अनुमान में उपयोग किया जाता है, उदाहरण के लिए परिकल्पना परीक्षण और आत्मविश्वास अंतराल में। हम नीचे देखेंगे कि इस प्रकार के संभाव्यता वितरण के अनुप्रयोग क्या हैं।

ची-स्क्वायर वितरण ग्राफ़

एक बार जब हम ची-स्क्वायर वितरण की परिभाषा देखते हैं, तो हम ग्राफिक रूप से दर्शाए गए इस प्रकार के वितरण के कई उदाहरण देखेंगे। तो नीचे आप देख सकते हैं कि ची-स्क्वायर वितरण की संभाव्यता प्लॉट स्वतंत्रता की डिग्री के आधार पर कैसे भिन्न होती है।

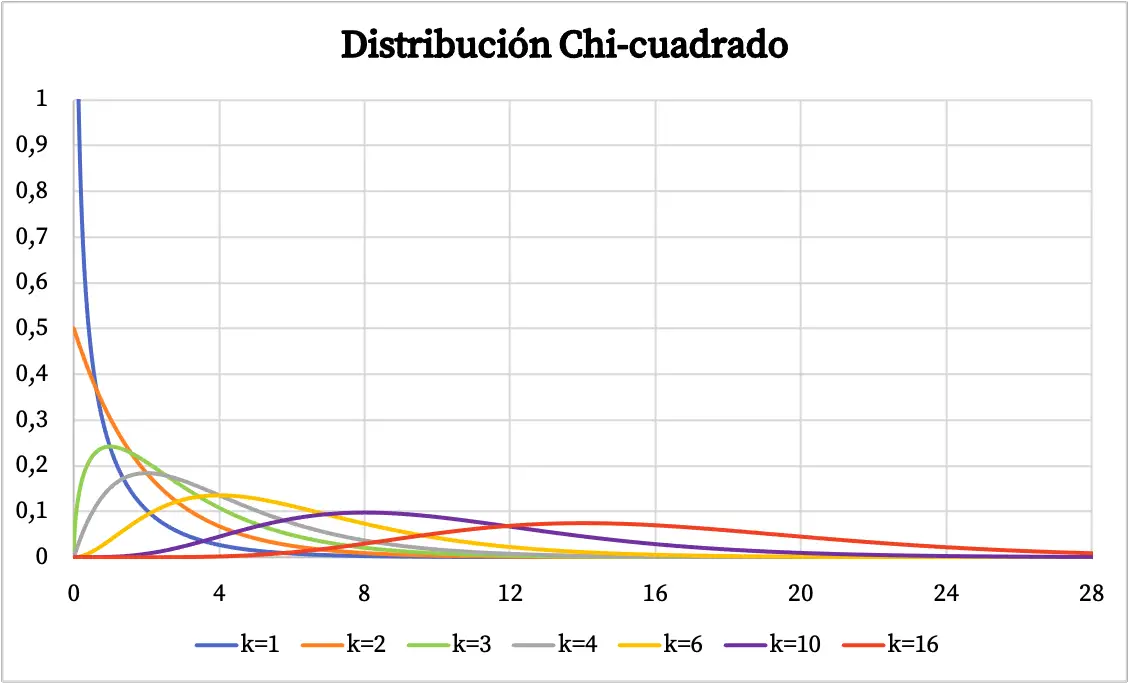
ची-स्क्वायर वितरण के घनत्व फ़ंक्शन को ऊपर दिए गए ग्राफ़ में दर्शाया गया है। दूसरी ओर, ची-स्क्वायर संचयी संभाव्यता वितरण फ़ंक्शन का ग्राफ इस प्रकार है:

➤ देखें: ची-स्क्वायर वितरण तालिका

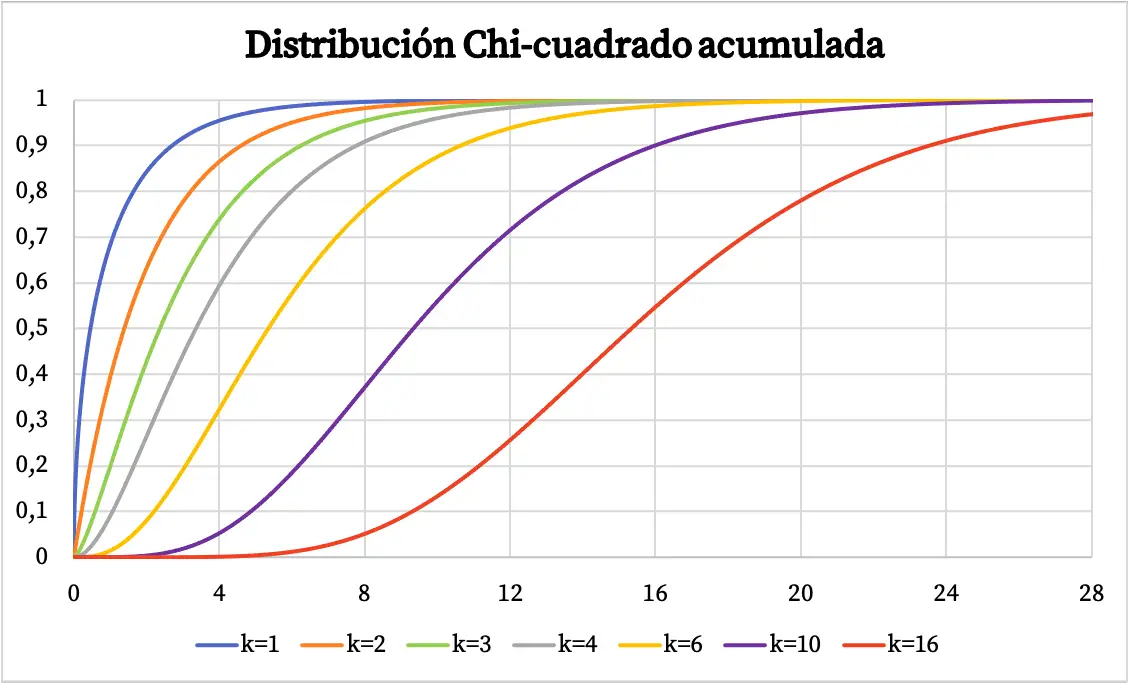
ची-वर्ग वितरण की विशेषताएँ

इस खंड में हम संभाव्यता सिद्धांत और सांख्यिकी से संबंधित ची-स्क्वायर वितरण के सबसे महत्वपूर्ण गुण देखेंगे।

ची-स्क्वायर वितरण का माध्य इसकी स्वतंत्रता की डिग्री के बराबर है।

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

ची-स्क्वायर वितरण का विचरण वितरण की स्वतंत्रता की डिग्री के दोगुने के बराबर है।

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

ची-स्क्वायर वितरण का मोड उसकी स्वतंत्रता की डिग्री से दो इकाइयाँ कम है, जब तक कि वितरण में स्वतंत्रता की एक डिग्री से अधिक हो।

$Mo=k-2 \qquad \text{si } k\geq 2$

यदि x=0 है तो ची-वर्ग वितरण का घनत्व फलन शून्य है। हालाँकि, 0 से अधिक x के मानों के लिए, ची-स्क्वायर वितरण का घनत्व फ़ंक्शन निम्नलिखित सूत्र द्वारा परिभाषित किया गया है:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

ची-स्क्वायर वितरण का संचयी वितरण फ़ंक्शन निम्नलिखित सूत्र द्वारा नियंत्रित होता है:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

ची-स्क्वायर वितरण का तिरछापन गुणांक आठ के भागफल के वर्गमूल को वितरण की स्वतंत्रता की डिग्री की संख्या से विभाजित किया जाता है।

$\displaystyle A=\sqrt{\frac{8}{k}}$

ची-स्क्वायर वितरण की कुर्टोसिस की गणना निम्नलिखित अभिव्यक्ति का उपयोग करके की जाती है:

$C=3+\cfrac{12}{k}$

केंद्रीय सीमा प्रमेय के कारण, यदि k पर्याप्त बड़ा है तो ची-स्क्वायर वितरण को सामान्य वितरण द्वारा अनुमानित किया जा सकता है।

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

ची-स्क्वायर वितरण के अनुप्रयोग

ची-स्क्वायर वितरण के सांख्यिकी में कई अलग-अलग अनुप्रयोग हैं। वास्तव में, यहां तक कि ची-स्क्वायर परीक्षण भी है जिसका उपयोग चर के बीच स्वतंत्रता और सैद्धांतिक वितरण के लिए फिट की अच्छाई की जांच करने के लिए किया जाता है। उदाहरण के लिए, ची-स्क्वायर परीक्षण का उपयोग यह निर्धारित करने के लिए किया जा सकता है कि नमूने का डेटा पॉइसन वितरण के अनुरूप है या नहीं।

रैखिक प्रतिगमन विश्लेषण में, ची-स्क्वायर वितरण का उपयोग सामान्य रूप से वितरित जनसंख्या के माध्य का अनुमान लगाने और रैखिक प्रतिगमन अध्ययन रेखा के ढलान का अनुमान लगाने के लिए भी किया जाता है।

अंत में, ची वर्ग वितरण भी स्नेडेकोर एफ वितरण के साथ अपने संबंधों के माध्यम से, विचरण के विश्लेषण में भाग लेता है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने