चेबीशेव का प्रमेय

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 संभावना शून्य टिप्पणियां

यह लेख बताता है कि चेबीशेव का प्रमेय क्या है। यहां आपको चेबीशेव प्रमेय सूत्र, एक हल किया गया अभ्यास और, इसके अलावा, एक ऑनलाइन चेबीशेव प्रमेय कैलकुलेटर मिलेगा। अंत में, यह चेबीशेव के प्रमेय और अनुभवजन्य नियम के बीच अंतर दिखाता है।

चेबीशेव का प्रमेय क्या है?

चेबीशेव का प्रमेय , जिसे चेबीशेव की असमानता के रूप में भी जाना जाता है, एक सांख्यिकीय नियम है जिसका उपयोग इस संभावना की गणना करने के लिए किया जाता है कि एक यादृच्छिक चर का मान उसके माध्य से एक निश्चित दूरी के भीतर होता है।

दूसरे शब्दों में, आंकड़ों में, चेबीशेव के प्रमेय का उपयोग इस संभावना को निर्धारित करने के लिए किया जाता है कि कोई मान एक आत्मविश्वास अंतराल के भीतर है।

इसके अतिरिक्त, चेबीशेव के प्रमेय का उपयोग अन्य सांख्यिकीय प्रमेयों, जैसे बड़ी संख्या के नियम, को सिद्ध करने के लिए भी किया जाता है।

हालाँकि चेबीशेव का प्रमेय पहली बार फ्रांसीसी इरेनी-जूल्स बिएनेमे द्वारा तैयार किया गया था, प्रमेय का नाम इसलिए रखा गया क्योंकि इसकी उत्पत्ति 1867 में रूसी पफ़नुटी चेबुशेव द्वारा की गई थी।

चेबीशेव प्रमेय का सूत्र

चेबीशेव का प्रमेय कहता है कि किसी मान के माध्य से k मानक विचलन के बराबर होने की संभावना k वर्ग से विभाजित अनुपात के एक ऋण से अधिक या उसके बराबर है।

इसलिए, चेबीशेव के प्रमेय का सूत्र इस प्रकार है:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\geq 1 -\frac{1}{k^2}$

सोना

$X$

यादृच्छिक चर का मान है,

$\mu$

चर का अंकगणितीय माध्य ,

$\sigma$

इसका मानक विचलन और

$k$

माध्य से मानक विचलन की संख्या जिस पर संभाव्यता की गणना की जानी है।

ध्यान दें कि इस सूत्र का उपयोग केवल तभी किया जा सकता है जब मानक विचलन की संख्या जिस पर गणना की जाती है वह 1 से अधिक है, या दूसरे शब्दों में, यदि k 1 से अधिक है।

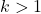$k>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”41″ style=”vertical-align: -2px;”></p> </p> <p> 👉 <u style=$ संभाव्यता की गणना करने के लिए आप नीचे दिए गए ऑनलाइन चेबीशेव प्रमेय कैलकुलेटर का उपयोग कर सकते हैं।

चेबीशेव के प्रमेय का उदाहरण

एक बार जब हमने चेबीशेव के प्रमेय की परिभाषा देख ली और इसका सूत्र क्या है, तो अवधारणा को बेहतर ढंग से समझने के लिए इस सांख्यिकीय प्रमेय का एक हल किया हुआ उदाहरण यहां दिया गया है।

यदि किसी विश्वविद्यालय के पाठ्यक्रम आँकड़ों में अर्जित ग्रेड को 65 के औसत और 10 के मानक विचलन के साथ वितरण द्वारा परिभाषित किया जाता है, तो कितने प्रतिशत छात्रों ने 50 और 80 के बीच ग्रेड अर्जित किया?

इस समस्या को हल करने के लिए, हमें चेबीशेव प्रमेय के सूत्र को लागू करने की आवश्यकता है। हालाँकि, हमें पहले यह निर्धारित करना होगा कि चर के माध्य से 50 और 80 मान कितने मानक विचलन हैं, ऐसा करने के लिए, हमें बस निम्नलिखित गणना करने की आवश्यकता है:

$k=\cfrac{\text{valor}-\text{media}}{\text{desviaci\'on t\'ipica}}$

$k=\cfrac{50-65}{10}=-1,5$

$k=\cfrac{80-65}{10}=1,5$

इसलिए, मान 50 और 80 क्रमशः निचले और ऊपरी माध्य से 1.5 मानक विचलन के अनुरूप हैं। इसलिए हम k=1.5 के साथ चेबीशेवा के प्रमेय के सूत्र का उपयोग करते हैं:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\leq 1 -\frac{1}{k^2}$

$\displaystyle P(\mu-1,5\sigma\leq X \leq \mu+1,5\sigma)\leq 1 -\frac{1}{1,5^2}$

$\displaystyle P(50\leq X \leq 80)\leq 0,5556$

इस प्रकार, कम से कम 55.56% छात्रों ने 50 और 80 के बीच ग्रेड प्राप्त किया।

चेबीशेव का प्रमेय कैलकुलेटर

प्रश्नगत मानों और माध्य (k) के बीच मानक विचलन की संख्या दर्ज करें, फिर “गणना करें” पर क्लिक करें। फिर कैलकुलेटर विश्वास अंतराल की न्यूनतम संभावना लौटाएगा।

आपको दशमलव विभाजक के रूप में बिंदु का उपयोग करके मानक विचलन की संख्या दर्ज करनी होगी।

चेबीशेव का प्रमेय और अंगूठे का नियम

सांख्यिकी में दो निकट से संबंधित अवधारणाएँ चेबीशेव का प्रमेय और अनुभवजन्य नियम हैं, क्योंकि दोनों का उपयोग आत्मविश्वास अंतराल की संभावना की गणना करने के लिए किया जाता है।

चेबीशेव के प्रमेय और अनुभवजन्य नियम के बीच अंतर यह है कि चेबीशेव के प्रमेय का उपयोग किसी भी प्रकार के वितरण पर किया जा सकता है, जबकि अनुभवजन्य नियम केवल सामान्य वितरण के लिए मान्य है।

चेबीशेव के प्रमेय का उपयोग इसलिए व्यापक है, लेकिन अनुभवजन्य नियम सामान्य वितरण के लिए अधिक सटीक परिणाम प्रदान करता है।

यह देखने के लिए यहां क्लिक करें कि वास्तव में अंगूठे का नियम क्या है:

➤ देखें: सामान्य नियम

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने