एक्सेल में चेबीशेव के प्रमेय को कैसे लागू करें

चेबीशेव के प्रमेय में कहा गया है कि 1 से अधिक किसी भी संख्या k के लिए, किसी भी प्रशिक्षित वितरण में डेटा मानों का कम से कम 1 – 1/k ² माध्य से k मानक विचलन के भीतर होता है।

उदाहरण के लिए, किसी भी आकार के वितरण के लिए, वितरण में कम से कम 1 – 1/3 ² = 88.89% मान माध्य के 3 मानक विचलन के भीतर आएंगे।

यह ट्यूटोरियल एक्सेल में चेबीशेव के प्रमेय को लागू करने के कई उदाहरण प्रदर्शित करता है।

उदाहरण 1: यह निर्धारित करने के लिए चेबीशेव के प्रमेय का उपयोग करें कि 50 के माध्य और 10 के मानक विचलन वाले डेटा सेट के लिए मानों का कितना प्रतिशत 30 और 70 के बीच आएगा।

सबसे पहले, k का मान ज्ञात करें। हम यह निर्धारित करके ऐसा कर सकते हैं कि माध्य से 30 और 70 के बीच कितने मानक विचलन हैं:

(30 – माध्य) / मानक विचलन = (30 – 50) / 10 = -20 / 10 = -2

(70 – माध्य) / मानक विचलन = (70 – 50) / 10 = 20 / 10 = 2

मान 30 और 70 क्रमशः माध्य से नीचे और ऊपर 2 मानक विचलन हैं। तो, k = 2 ।

फिर हम इस डेटा सेट के माध्य के 2 मानक विचलन के भीतर आने वाले मानों का न्यूनतम प्रतिशत खोजने के लिए एक्सेल में निम्नलिखित सूत्र का उपयोग कर सकते हैं:

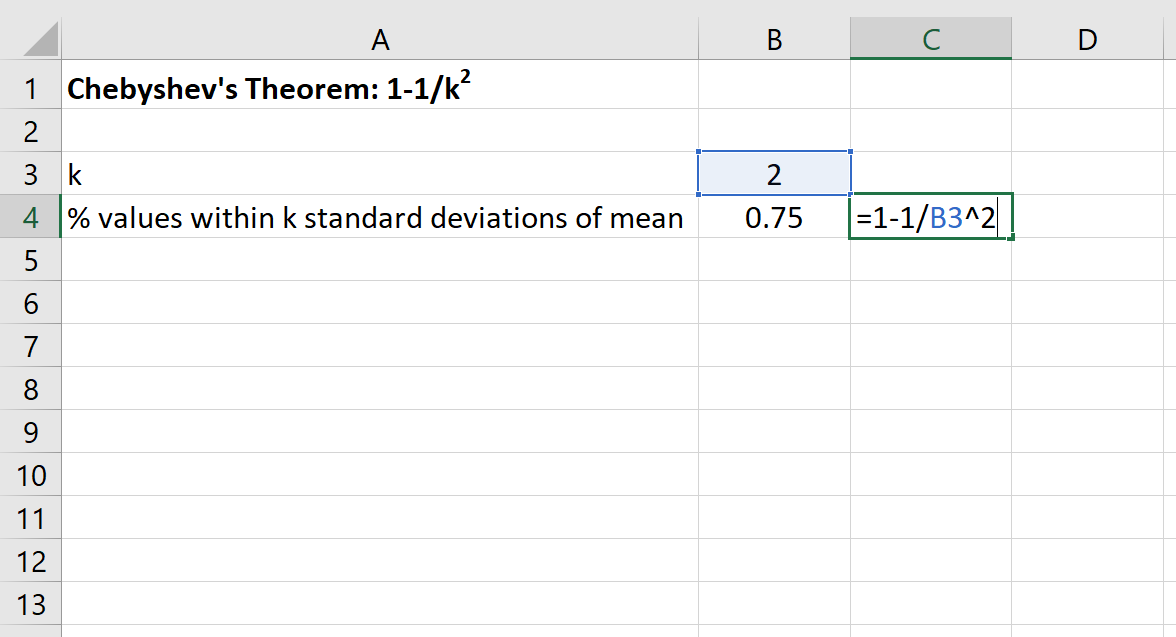
इस डेटासेट के लिए 30 और 70 के बीच मानों का प्रतिशत कम से कम 75% होगा।

उदाहरण 2: 35 के माध्य और 5 के मानक विचलन वाले डेटा सेट के लिए 20 और 50 के बीच कितने प्रतिशत मान गिरेंगे, यह निर्धारित करने के लिए चेबीशेव के प्रमेय का उपयोग करें।

सबसे पहले, k का मान ज्ञात करें। हम यह निर्धारित करके ऐसा कर सकते हैं कि माध्य से 20 और 50 के बीच कितने मानक विचलन हैं:

(20 – माध्य) / मानक विचलन = (20 – 35) / 5 = -15 / 5 = -3

(50 – माध्य) / मानक विचलन = (50 – 35) / 5 = 15 / 5 = 3

मान 20 और 50 क्रमशः माध्य से नीचे और ऊपर 3 मानक विचलन हैं। तो, k = 3 ।

फिर हम इस डेटा सेट के माध्य के 3 मानक विचलन के भीतर आने वाले मानों का न्यूनतम प्रतिशत ज्ञात करने के लिए एक्सेल में निम्नलिखित सूत्र का उपयोग कर सकते हैं:

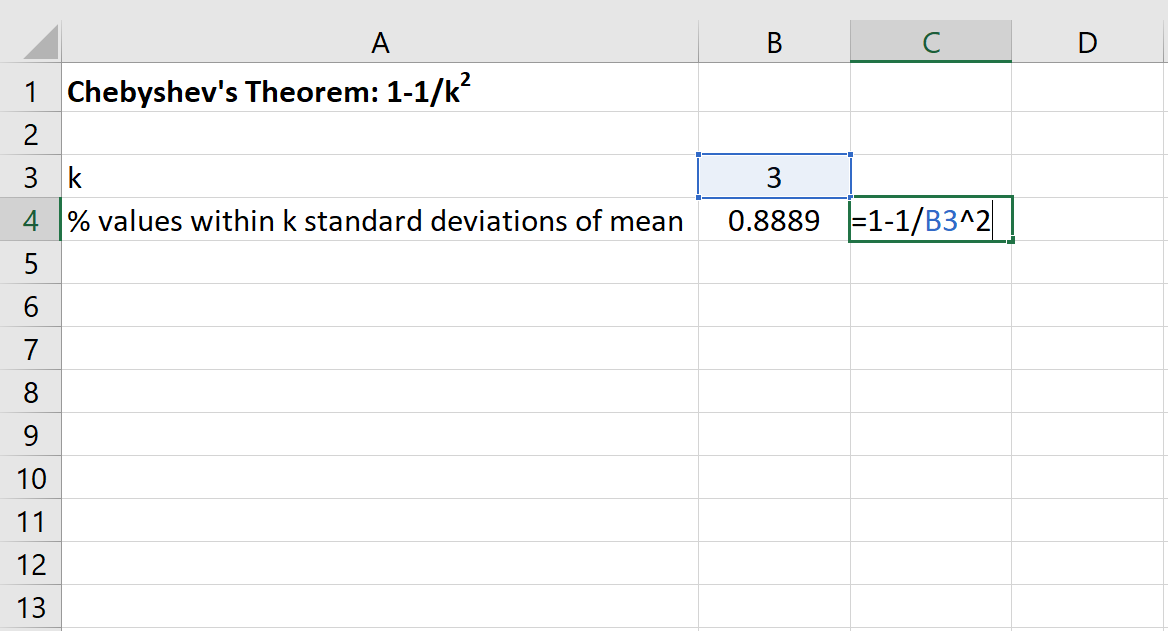
इस डेटासेट के लिए 20 और 50 के बीच मानों का प्रतिशत कम से कम 88.89% होगा।

उदाहरण 3: 100 के माध्य और 5 के मानक विचलन वाले डेटा सेट के लिए 80 और 120 के बीच कितने प्रतिशत मान गिरेंगे, यह निर्धारित करने के लिए चेबीशेव के प्रमेय का उपयोग करें।

सबसे पहले, k का मान ज्ञात करें। हम यह निर्धारित करके यह कर सकते हैं कि माध्य से 80 और 120 के बीच कितने मानक विचलन हैं:

(80 – माध्य) / मानक विचलन = (80 – 100) / 5 = -20 / 5 = -4

(120 – माध्य) / मानक विचलन = (120 – 100) / 5 = 20 / 5 = 4

80 और 120 मान क्रमशः माध्य से नीचे और ऊपर 4 मानक विचलन हैं। तो, k = 4 ।

फिर हम इस डेटा सेट के माध्य के 4 मानक विचलन के भीतर आने वाले मानों का न्यूनतम प्रतिशत ज्ञात करने के लिए एक्सेल में निम्नलिखित सूत्र का उपयोग कर सकते हैं:

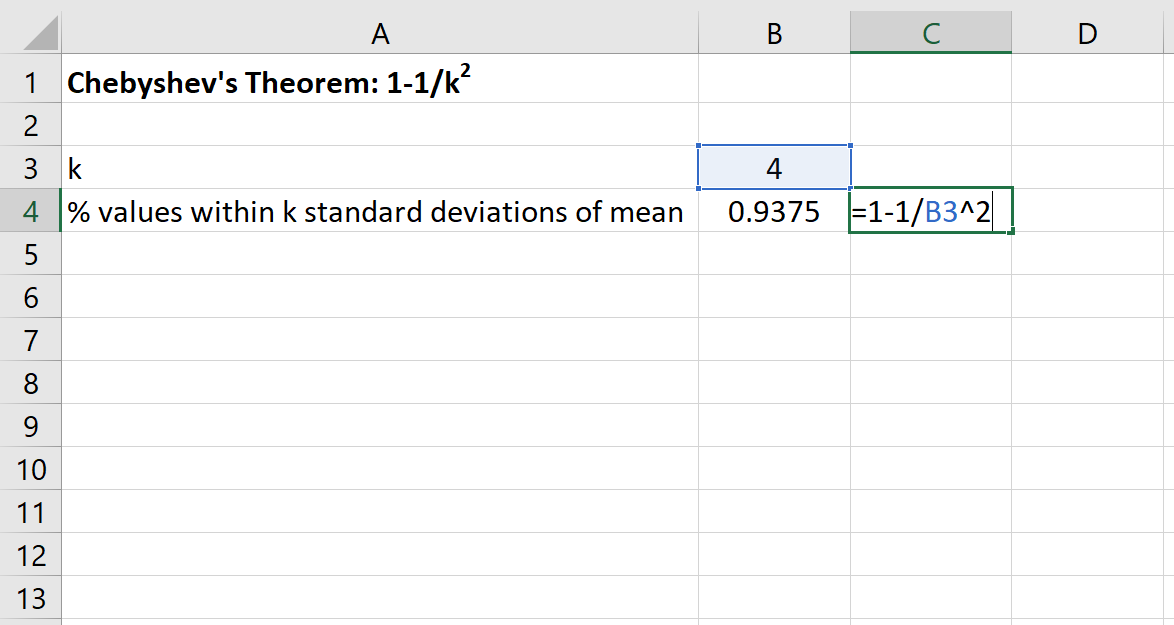
इस डेटासेट के लिए 80 और 120 के बीच मानों का प्रतिशत कम से कम 93.75% होगा।