ज्यामितीय वितरण का परिचय

ज्यामितीय वितरण बर्नौली परीक्षणों की श्रृंखला में पहली सफलता का अनुभव करने से पहले एक निश्चित संख्या में विफलताओं का अनुभव करने की संभावना का वर्णन करता है।

बर्नौली परीक्षण केवल दो संभावित परिणामों वाला एक प्रयोग है – “सफलता” या “असफलता” – और हर बार प्रयोग आयोजित होने पर सफलता की संभावना समान होती है।

बर्नौली निबंध का एक उदाहरण सिक्का उछालना है। सिक्का केवल दो चित पर गिर सकता है (हम चित को “हिट” और पट को “विफलता” कह सकते हैं) और प्रत्येक फ्लिप पर सफलता की संभावना 0.5 है, यह मानते हुए कि सिक्का उचित है।

यदि एक यादृच्छिक चर X एक ज्यामितीय वितरण का अनुसरण करता है, तो पहली सफलता का अनुभव करने से पहले k विफलताओं का अनुभव करने की संभावना निम्नलिखित सूत्र द्वारा पाई जा सकती है:

पी(एक्स=के) = (1-पी) ^केपी

सोना:

• k: पहली सफलता से पहले विफलताओं की संख्या
• पी: प्रत्येक परीक्षण पर सफलता की संभावना

उदाहरण के लिए, मान लें कि हम जानना चाहते हैं कि एक सिक्के को हेड आने तक हमें कितनी बार उछालना होगा। हम 0, 1, 2, 3 विफलताओं आदि का अनुभव करने की संभावना निर्धारित करने के लिए उपरोक्त सूत्र का उपयोग कर सकते हैं। इससे पहले कि सिक्का सिर पर गिरे:

ध्यान दें: यदि सिक्का पहली बार उछालने पर शीर्ष पर आता है तो उसे 0 “विफलता” का अनुभव हो सकता है।

पी(एक्स=0) = (1-.5) ⁰ (.5) = 0.5

पी(एक्स=1) = (1-.5) ¹ (.5) = 0.25

पी(एक्स=2) = (1-.5) ² (.5) = 0.125

पी(एक्स=3) = (1-0.5) ³ (0.5) = 0.0625

हम अनंत तक किसी भी संख्या में सिक्के उछाले जाने की प्रायिकता की गणना कर सकते हैं। फिर हम इस संभाव्यता वितरण की कल्पना करने के लिए एक सरल हिस्टोग्राम बनाते हैं:

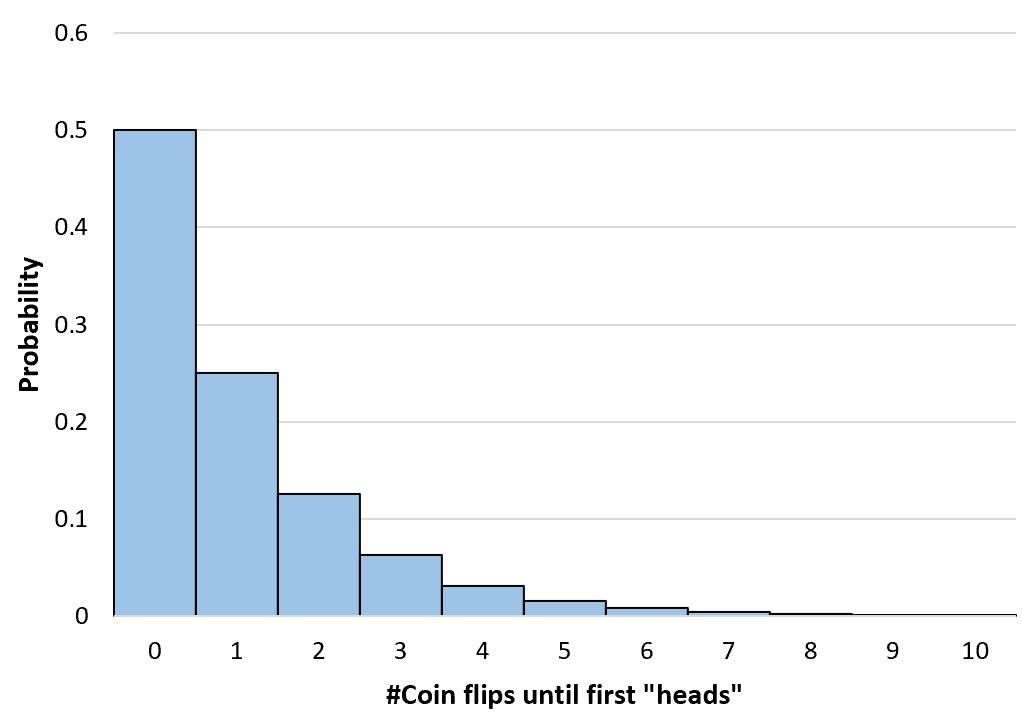
संचयी ज्यामितीय संभावनाओं की गणना

पहली सफलता तक हमें k या उससे कम विफलताओं का अनुभव होने की संचयी संभावना निम्नलिखित सूत्र द्वारा पाई जा सकती है:

P(X≤k) = 1 – (1-p) ^k+1

सोना:

• k: पहली सफलता से पहले विफलताओं की संख्या
• पी: प्रत्येक परीक्षण पर सफलता की संभावना

उदाहरण के लिए, मान लीजिए कि हम इस संभावना को जानना चाहते हैं कि सिक्का अंततः सिर पर आने से पहले तीन या उससे कम “मिस” करेगा। इस संभाव्यता की गणना के लिए हम निम्नलिखित सूत्र का उपयोग करेंगे:

पी(एक्स≤3) = 1 – (1-0.5) ³⁺¹ = 0.9375

हम समान सूत्र का उपयोग करके प्रत्येक संचयी संभावना की गणना कर सकते हैं:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0.5) ¹⁺¹ = 0.75

पी(एक्स≤2) = 1 – (1-0.5) ²⁺¹ = 0.875

हम अनंत तक सिक्के उछालने की किसी भी संख्या के लिए इन संचयी संभावनाओं की गणना कर सकते हैं। फिर हम इस संचयी संभाव्यता वितरण को देखने के लिए एक हिस्टोग्राम बना सकते हैं:

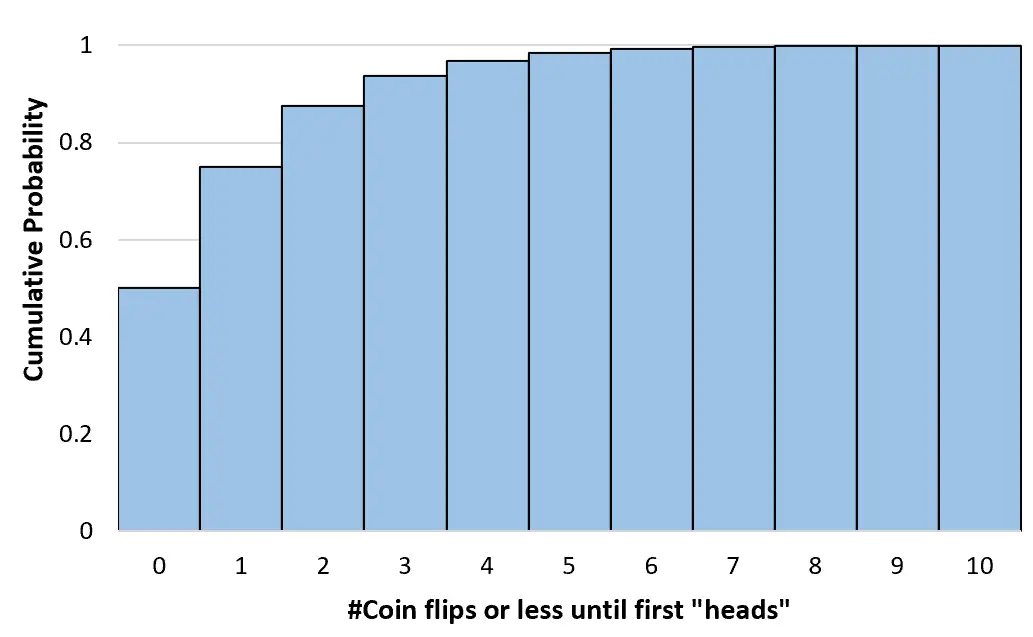
ज्यामितीय वितरण के गुण

ज्यामितीय वितरण में निम्नलिखित गुण हैं:

वितरण का माध्य (1-p)/p है।

वितरण का विचरण (1-पी)/पी ² है।

उदाहरण के लिए:

हम उम्मीद करते हैं कि किसी सिक्के के टेल में आने से पहले वह औसतन कितनी बार हेड पर आएगा (1-p) / p = (1-.5) / .5 = 1 ।

जब तक यह सिर पर नहीं गिरता तब तक उछालने की संख्या में अंतर (1-p)/ ^p2 =(1-.5)/ होगा। ⁵² = 2 .

ज्यामितीय वितरण अभ्यास समस्याएं

ज्यामितीय वितरण के अपने ज्ञान का परीक्षण करने के लिए निम्नलिखित अभ्यास समस्याओं का उपयोग करें।

नोट: हम इन प्रश्नों के उत्तर की गणना के लिए ज्यामितीय वितरण कैलकुलेटर का उपयोग करेंगे।

समस्या 1

प्रश्न: एक शोधकर्ता लोगों से यह पूछने के लिए पुस्तकालय के बाहर इंतजार कर रहा है कि क्या वे किसी निश्चित कानून का समर्थन करते हैं। किसी व्यक्ति द्वारा कानून का समर्थन करने की प्रायिकता p = 0.2 है। इसकी क्या संभावना है कि शोधकर्ता जिस चौथे व्यक्ति से बात करेगा वह कानून का समर्थन करने वाला पहला व्यक्ति होगा?

उत्तर: पहली सफलता तक “असफलताओं” की संख्या – यानी, ऐसे लोगों की संख्या जो कानून का समर्थन नहीं करते जब तक कि पहला व्यक्ति इसका समर्थन नहीं करता – 3 है। इसलिए, पी = 0.2 और एक्स के साथ ज्यामितीय वितरण कैलकुलेटर का उपयोग करने में = 3 विफलताएँ, हम पाते हैं कि P(X=3) = 0.10240 ।

समस्या 2

प्रश्न: एक शोधकर्ता लोगों से यह पूछने के लिए पुस्तकालय के बाहर इंतजार कर रहा है कि क्या वे किसी निश्चित कानून का समर्थन करते हैं। किसी व्यक्ति द्वारा कानून का समर्थन करने की प्रायिकता p = 0.2 है। इसकी क्या संभावना है कि कानून का समर्थन करने वाले किसी व्यक्ति को खोजने के लिए शोधकर्ता को चार से अधिक लोगों से बात करनी पड़ेगी?

उत्तर: p =0.2 और x = 4 विफलताओं के साथ ज्यामितीय वितरण कैलकुलेटर का उपयोग करते हुए, हम पाते हैं कि P(X>4) = 0.32768 ।

समस्या 3

प्रश्न: एक शोधकर्ता लोगों से यह पूछने के लिए पुस्तकालय के बाहर इंतजार कर रहा है कि क्या वे किसी निश्चित कानून का समर्थन करते हैं। किसी व्यक्ति द्वारा कानून का समर्थन करने की प्रायिकता p = 0.2 है। शोधकर्ता को तब तक कितने लोगों से बात करने की अपेक्षित संख्या की आवश्यकता होगी जब तक उसे कोई ऐसा व्यक्ति न मिल जाए जो कानून का समर्थन करता हो?

उत्तर: याद रखें कि ज्यामितीय वितरण का माध्य (1-पी)/पी है। इस स्थिति में, औसत (1-.2) / .2 = 4 होगा।