झगड़ा

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

इस लेख में हम बताते हैं कि विचरण, जिसे विचरण भी कहा जाता है, क्या है और इसकी गणना कैसे की जाती है। आपको विचरण सूत्र मिलेगा, विचरण गणना का एक ठोस उदाहरण और, इसके अलावा, आप ऑनलाइन कैलकुलेटर के साथ किसी भी डेटा सेट के विचरण की गणना करने में सक्षम होंगे।

हम आपको यह भी दिखाते हैं कि समूहीकृत डेटा का विचरण कैसे खोजा जाए, क्योंकि यह एक अलग तरीके से किया जाता है। अंत में, हम आपको जनसंख्या विचरण और नमूना विचरण के बीच अंतर, विचरण और मानक विचलन के बीच अंतर और इस सांख्यिकीय माप के गुण सिखाते हैं।

विचरण क्या है?

सांख्यिकी में, विचरण फैलाव का एक माप है जो एक यादृच्छिक चर की परिवर्तनशीलता को इंगित करता है। यह प्रसरण अवशिष्टों के वर्गों के योग को प्रेक्षणों की कुल संख्या से विभाजित करने के बराबर है।

ध्यान रखें कि अवशिष्ट को सांख्यिकीय डेटा बिंदु के मान और डेटा सेट के माध्य के बीच अंतर के रूप में समझा जाता है।

संभाव्यता सिद्धांत में, विचरण का प्रतीक ग्रीक अक्षर सिग्मा स्क्वायर (σ ² ) है। हालाँकि इसे आमतौर पर Var(X) के रूप में भी दर्शाया जाता है, X एक यादृच्छिक चर है जिससे विचरण की गणना की जाती है।

सामान्य तौर पर, यादृच्छिक चर के विचरण मान की व्याख्या करना सरल है। विचरण मान जितना बड़ा होगा, डेटा उतना अधिक बिखरा हुआ होगा। और इसके विपरीत, विचरण मान जितना छोटा होगा, डेटा श्रृंखला में फैलाव उतना ही कम होगा। हालाँकि, विचरण की व्याख्या करते समय, व्यक्ति को आउटलेर्स से सावधान रहना चाहिए, क्योंकि वे विचरण मान को विकृत कर सकते हैं।

विचरण, विचरण के अलावा जिन अन्य मापों पर विचार किया जाता है वे हैं सीमा, मानक विचलन, माध्य विचलन और भिन्नता का गुणांक।

अंतर की गणना कैसे करें

विचरण की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

डेटा सेट का अंकगणितीय माध्य ज्ञात करें।
डेटा सेट के मूल्यों और माध्य के बीच अंतर के रूप में परिभाषित अवशेषों की गणना करें।
प्रत्येक शेष का वर्ग करें।
पिछले चरण में गणना किए गए सभी परिणाम जोड़ें।
डेटा की कुल संख्या से विभाजित करें. प्राप्त परिणाम डेटा श्रृंखला का विचरण है।

अंत में, डेटा सेट के विचरण की गणना करने का सूत्र है:

सोना:

$X$

वह यादृच्छिक चर है जिसके लिए आप विचरण की गणना करना चाहते हैं।
$x_i$

डेटा मान है

$i$

.
$n$

प्रेक्षणों की कुल संख्या है.
$\overline{X}$

यादृच्छिक चर का माध्य है

$X$

.

👉 आप किसी भी डेटा सेट के विचरण की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

इसलिए, डेटा श्रृंखला से भिन्नता निकालने के लिए, यह आवश्यक है कि आप जानें कि अंकगणितीय माध्य की गणना कैसे की जाती है। यदि आपको यह याद नहीं है कि यह कैसे करना है, तो आप इसे ऊपर लिंक किए गए लेख में देख सकते हैं।

विचलन का उदाहरण

अब जब हम विचरण की परिभाषा जानते हैं, तो हम चरण दर चरण एक अभ्यास को हल करेंगे ताकि आप देख सकें कि डेटा श्रृंखला का विचरण कैसे प्राप्त किया जाता है।

एक बहुराष्ट्रीय कंपनी से, पिछले पांच वर्षों में उसके आर्थिक परिणाम ज्ञात हैं, अधिकांश में उसने लाभ प्राप्त किया लेकिन एक वर्ष में उसे काफी घाटा हुआ: 11.5, 2, -9, 7 मिलियन यूरो। इस डेटा सेट के विचरण की गणना करें।

जैसा कि हमने उपरोक्त स्पष्टीकरण में देखा, किसी डेटा श्रृंखला का विचरण ज्ञात करने के लिए सबसे पहली चीज़ जो हमें करने की ज़रूरत है वह है इसके अंकगणितीय माध्य की गणना करना:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

और एक बार जब हमें डेटा का औसत मूल्य पता चल जाता है, तो हम विचरण सूत्र का उपयोग कर सकते हैं:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

हम अभ्यास विवरण द्वारा प्रदान किए गए डेटा को सूत्र में प्रतिस्थापित करते हैं:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

अंत में, जो कुछ बचा है वह विचरण की गणना करने के लिए ऑपरेशन को हल करना है:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

ध्यान दें कि विचरण इकाइयाँ सांख्यिकीय डेटा की समान इकाइयाँ हैं लेकिन वर्गित हैं, इस कारण से इस डेटा समूह का विचरण 45.76 मिलियन यूरो ² है।

गैप कैलकुलेटर

इसके विचरण की गणना करने के लिए निम्नलिखित कैलकुलेटर में एक सांख्यिकीय डेटा सेट दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

समूहीकृत डेटा के लिए भिन्नता

अंतरालों में समूहीकृत डेटा के विचरण की गणना करने के लिए , निम्नलिखित चरणों का पालन किया जाना चाहिए:

समूहीकृत आँकड़ों का माध्य ज्ञात कीजिए।
समूहीकृत डेटा के अवशेषों की गणना करें।
प्रत्येक शेष का वर्ग करें।
प्रत्येक पिछले परिणाम को उसके अंतराल की आवृत्ति से गुणा करें।
पिछले चरण में प्राप्त सभी मानों का योग जोड़ें।
प्रेक्षणों की कुल संख्या से विभाजित करें. परिणामी संख्या समूहीकृत डेटा का विचरण है।

दूसरे शब्दों में, अंतरालों में समूहीकृत डेटा के विचरण की गणना करने का सूत्र इस प्रकार है:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

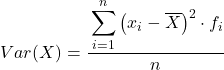
हालाँकि उपरोक्त सूत्र सामान्य रूप से उपयोग किया जाता है, नीचे दिए गए बीजगणितीय अभिव्यक्ति का भी उपयोग किया जा सकता है क्योंकि यह समतुल्य है:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

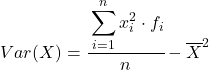
उदाहरण के तौर पर, हम निम्नलिखित समूहीकृत डेटा श्रृंखला का विचरण पाएंगे:

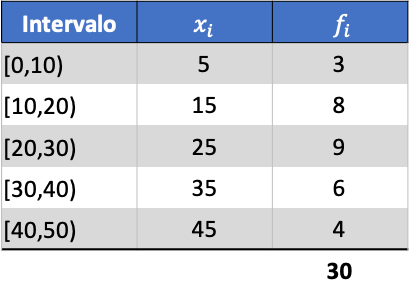
सबसे पहले, हमें समूहीकृत डेटा का औसत निर्धारित करने की आवश्यकता है। ऐसा करने के लिए, हम आवृत्ति तालिका में वर्ग चिह्न और आवृत्ति के उत्पाद के साथ एक कॉलम जोड़ते हैं:

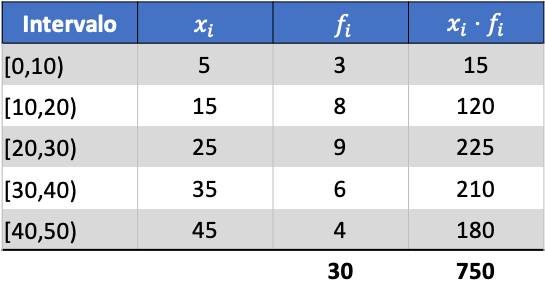
अब हम जोड़े गए कॉलम के योग को डेटा की कुल संख्या से विभाजित करके समूहीकृत डेटा के औसत की गणना करते हैं:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

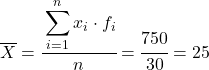
और परिकलित डेटा के औसत से, हम निम्नलिखित तीन कॉलम जोड़ सकते हैं:

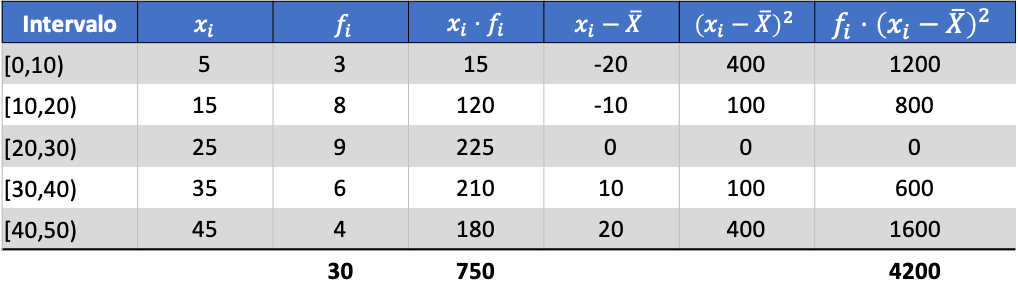
तो एकत्रित डेटा सेट का विचरण, देखे गए डेटा की कुल संख्या से विभाजित अंतिम कॉलम का योग है:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

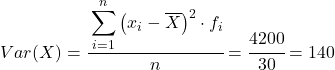
विचरण और मानक विचलन

भिन्नता और मानक विचलन (या मानक विचलन) फैलाव के दो उपाय हैं और इसलिए दोनों डेटा सेट के फैलाव की डिग्री का संकेत देते हैं। हालाँकि, विचरण और मानक विचलन के बीच अंतर यह है कि सामान्य रूप से विचरण का मान बड़ा होता है, क्योंकि यह मानक विचलन का वर्ग है।

मानक विचलन को आम तौर पर ग्रीक अक्षर सिग्मा (σ) द्वारा दर्शाया जाता है, और इस कारण से विचरण को अक्षर सिग्मा वर्ग (σ ² ) द्वारा दर्शाया जाता है, क्योंकि यह गणितीय संबंध है जो इन दो फैलाव मैट्रिक्स के बीच मौजूद है।

$Var(X)=\sigma^2$

इसलिए, एक बार जब आप डेटा के एक सेट के विचरण मान की गणना कर लेते हैं, तो आप केवल विचरण का वर्गमूल लेकर उसी सेट का मानक विचलन मान आसानी से पा सकते हैं।

$\sigma=\sqrt{\sigma^2}$

जनसंख्या भिन्नता और नमूना भिन्नता

तार्किक रूप से, जनसंख्या विचरण एक सांख्यिकीय जनसंख्या के विचरण की गणना को संदर्भित करता है और इसके बजाय, नमूना विचरण को एक नमूने के विचरण की गणना के लिए लागू किया जाता है। हालाँकि, ये दो अलग-अलग अवधारणाएँ हैं क्योंकि जनसंख्या विचरण सूत्र नमूना विचरण सूत्र से भिन्न है।

आम तौर पर विचरण अभ्यास में, यदि वे हमें अन्यथा नहीं बताते हैं, तो प्रदान किए गए डेटा सेट के विचरण को खोजने के लिए हमें जनसंख्या विचरण सूत्र का उपयोग करना होगा, जिसे हमने लेख की शुरुआत में समझाया था:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

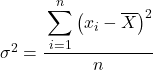
लेकिन शायद कुछ समस्याओं में आपसे सांख्यिकीय डेटा को एक नमूने के रूप में मानने के लिए कहा जाता है, ऐसी स्थिति में हमें नमूना विचरण सूत्र का उपयोग करने की आवश्यकता होती है:

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

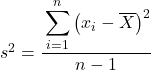
ध्यान दें कि यह इंगित करने के लिए कि जनसंख्या भिन्नता की गणना की जा रही है, इसे ग्रीक अक्षर σ द्वारा दर्शाया गया है, लेकिन जब नमूना भिन्नता की गणना की जा रही है, तो अक्षर s का उपयोग किया जाता है।

जैसा कि आप देख सकते हैं, दोनों सूत्रों के बीच एकमात्र अंतर यह है कि एक नमूने के भिन्नता में हमें कुल अवलोकनों की संख्या शून्य से 1 से विभाजित करने की आवश्यकता है, उदाहरण के लिए, यदि कुल 30 डेटा आइटम हैं, तो हम 29 से विभाजित करेंगे लेकिन अंश की गणना बिल्कुल उसी तरह से की जाती है।

विचरण गुण

विचरण में निम्नलिखित गुण हैं:

किसी भी यादृच्छिक चर का विचरण हमेशा शून्य से अधिक या उसके बराबर होगा। इसी तरह, यदि विचरण शून्य है, तो इसका मतलब है कि सभी सांख्यिकीय डेटा समान हैं।

$Var(x)\ge 0$

जाहिर है, एकल मान का प्रसरण शून्य है।

$Var(a)=0\qquad a\in \mathbb{R}$

एक चर द्वारा एक अदिश के गुणनफल का प्रसरण उस अदिश के चर के प्रसरण के वर्ग गुणा के बराबर होता है।

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

दो आश्रित चरों के योग का प्रसरण प्रत्येक चर के अलग-अलग प्रसरण के योग के साथ-साथ दोनों चरों के बीच सहप्रसरण के दोगुने के बराबर होता है।

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

नतीजतन, यदि दो चर स्वतंत्र हैं, तो उनके योग का प्रसरण निर्धारित करने के लिए उनके प्रसरणों को जोड़ना पर्याप्त है:

$Var(X+Y)=Var(X)+Var(Y)$

विचलन को निम्नलिखित सूत्र का उपयोग करके गणितीय अपेक्षा से भी परिभाषित किया जा सकता है:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने