डेटा को r (लॉग, स्क्वायर रूट, क्यूब रूट) में कैसे बदलें
कई सांख्यिकीय परीक्षण मानते हैं कि प्रतिक्रिया चर के अवशेष सामान्य रूप से वितरित होते हैं।
हालाँकि, अवशेष अक्सर सामान्य रूप से वितरित नहीं होते हैं। इस समस्या को हल करने का एक तरीका तीन परिवर्तनों में से एक का उपयोग करके प्रतिक्रिया चर को बदलना है:
1. लॉग परिवर्तन: प्रतिक्रिया चर को y से log(y) में बदलें।
2. वर्गमूल परिवर्तन: प्रतिक्रिया चर को y से √y में बदलें।
3. घनमूल परिवर्तन: प्रतिक्रिया चर को y से y 1/3 में बदलें।
इन परिवर्तनों को निष्पादित करके, प्रतिक्रिया चर आम तौर पर सामान्य वितरण का अनुमान लगाता है। निम्नलिखित उदाहरण दिखाते हैं कि आर में इन परिवर्तनों को कैसे निष्पादित किया जाए।
आर में लॉग परिवर्तन
निम्नलिखित कोड दिखाता है कि प्रतिक्रिया चर पर लॉग परिवर्तन कैसे करें:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform log transformation log_y <- log10(df$y)
निम्नलिखित कोड दिखाता है कि लॉग परिवर्तन करने से पहले और बाद में y के वितरण को प्रदर्शित करने के लिए हिस्टोग्राम कैसे बनाया जाए:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for log-transformed distribution hist(log_y, col='coral2', main='Log Transformed')
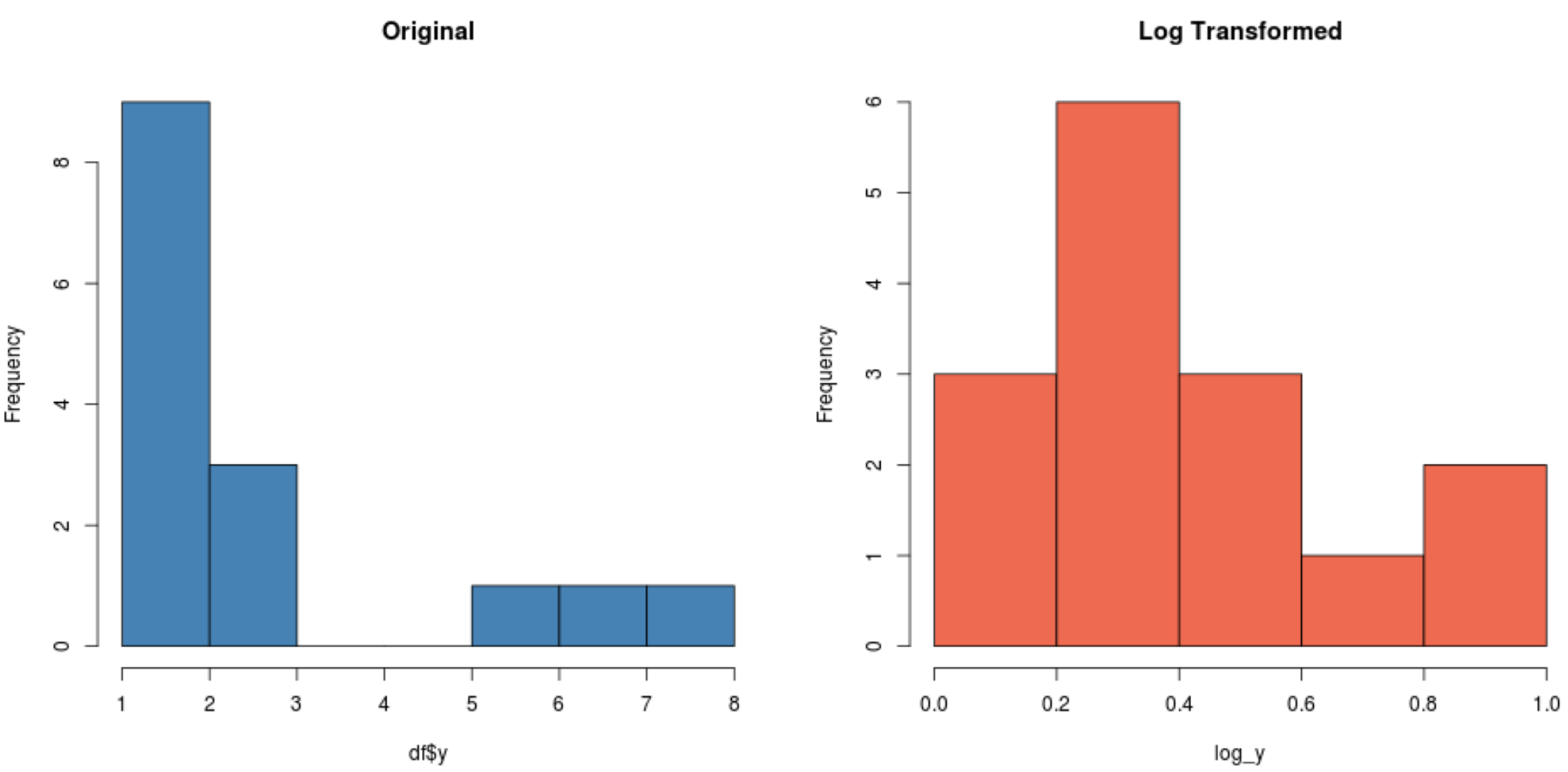
ध्यान दें कि कैसे लॉग-रूपांतरित वितरण मूल वितरण की तुलना में कहीं अधिक सामान्य है। यह अभी भी एक आदर्श “घंटी आकार” नहीं है, लेकिन यह मूल वितरण की तुलना में सामान्य वितरण के करीब है।
वास्तव में, यदि हम प्रत्येक वितरण पर शापिरो-विल्क परीक्षण करते हैं, तो हम पाएंगे कि मूल वितरण सामान्यता धारणा में विफल रहता है, जबकि लॉग-रूपांतरित वितरण (α = 0.05 पर) नहीं करता है:
#perform Shapiro-Wilk Test on original data shapiro.test(df$y) Shapiro-Wilk normality test data: df$y W = 0.77225, p-value = 0.001655 #perform Shapiro-Wilk Test on log-transformed data shapiro.test(log_y) Shapiro-Wilk normality test data:log_y W = 0.89089, p-value = 0.06917
आर में वर्गमूल परिवर्तन
निम्नलिखित कोड दिखाता है कि प्रतिक्रिया चर पर वर्गमूल परिवर्तन कैसे करें:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation sqrt_y <- sqrt(df$y)
निम्नलिखित कोड दिखाता है कि वर्गमूल परिवर्तन करने से पहले और बाद में y के वितरण को प्रदर्शित करने के लिए हिस्टोग्राम कैसे बनाया जाए:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(sqrt_y, col='coral2', main='Square Root Transformed')
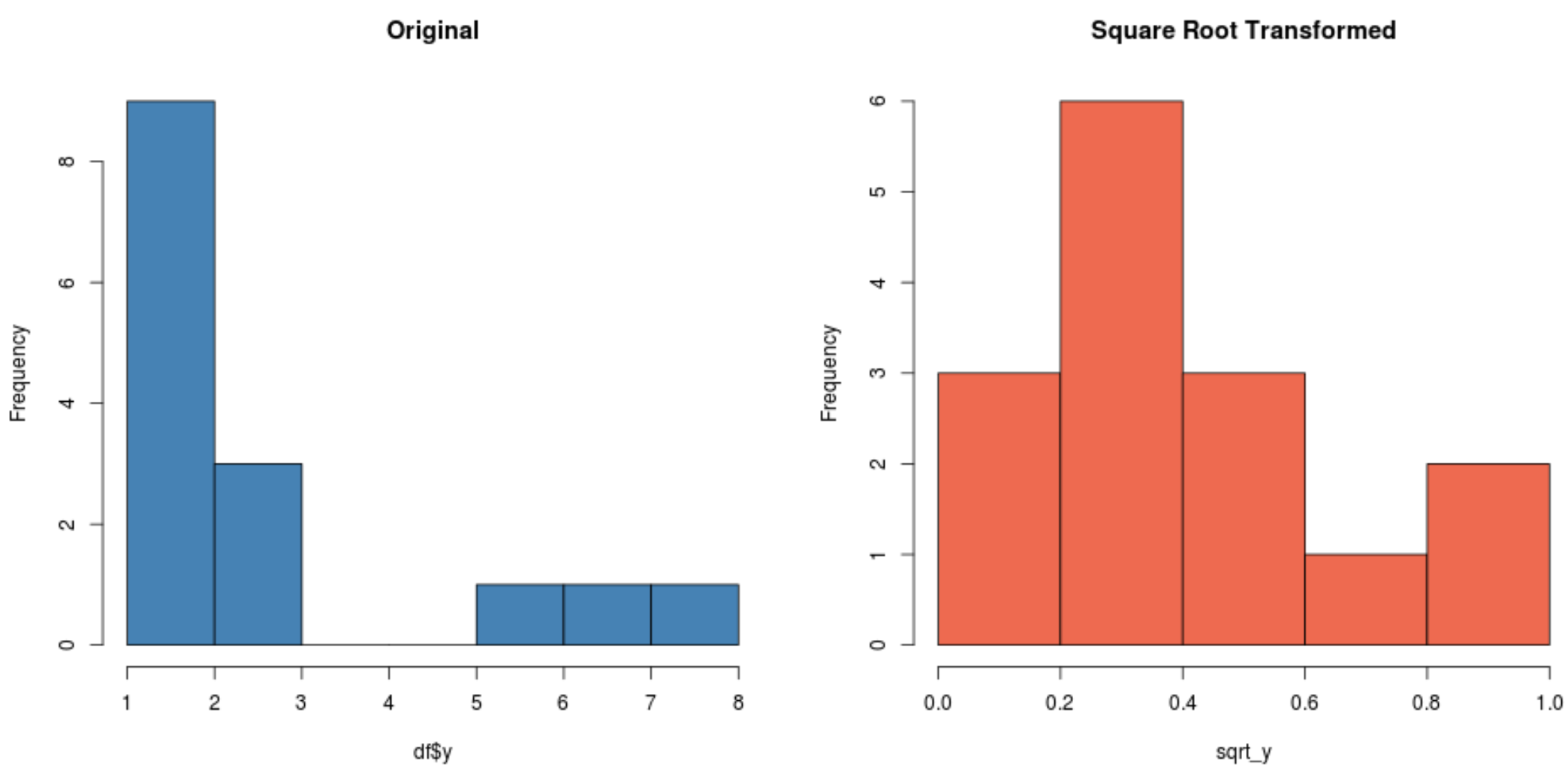
ध्यान दें कि कैसे वर्गमूल रूपांतरित वितरण मूल वितरण की तुलना में कहीं अधिक सामान्य रूप से वितरित होता है।
आर में घनमूल परिवर्तन
निम्नलिखित कोड दिखाता है कि प्रतिक्रिया चर पर क्यूब रूट परिवर्तन कैसे करें:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation cube_y <- df$y^(1/3)
निम्नलिखित कोड दिखाता है कि वर्गमूल परिवर्तन करने से पहले और बाद में y के वितरण को प्रदर्शित करने के लिए हिस्टोग्राम कैसे बनाया जाए:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(cube_y, col='coral2', main='Cube Root Transformed')
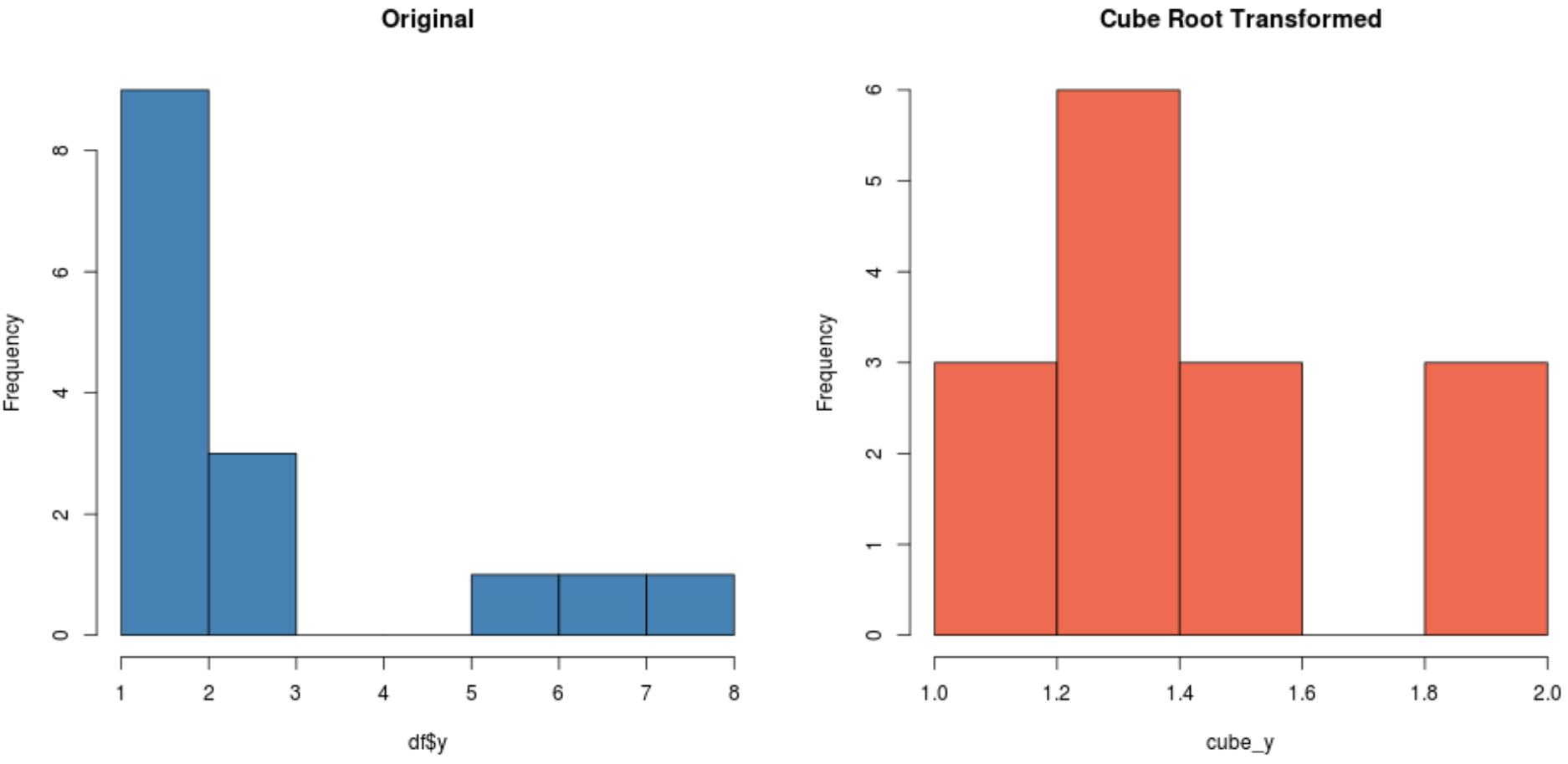
आपके डेटासेट के आधार पर, इनमें से एक परिवर्तन एक नया डेटासेट उत्पन्न कर सकता है जो अन्य की तुलना में अधिक सामान्य रूप से वितरित होता है।