थ्री-वे एनोवा: परिभाषा और उदाहरण

तीन-तरफा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन अलग-अलग कारक प्रतिक्रिया चर को कैसे प्रभावित करते हैं।

तीन-तरफ़ा एनोवा एक-तरफ़ा एनोवा (केवल एक कारक के साथ) या दो-तरफ़ा एनोवा (केवल दो कारकों के साथ) की तुलना में कम आम हैं, लेकिन वे अभी भी विभिन्न क्षेत्रों में उपयोग किए जाते हैं।

जब भी हम तीन-तरफ़ा एनोवा निष्पादित करते हैं, तो हम जानना चाहते हैं कि क्या प्रत्येक कारक और प्रतिक्रिया चर के बीच कोई सांख्यिकीय रूप से महत्वपूर्ण संबंध है, साथ ही क्या कारकों के बीच कोई अंतःक्रिया प्रभाव है।

यह ट्यूटोरियल कई परिदृश्य दिखाता है जिसमें आप तीन-तरफा एनोवा का उपयोग कर सकते हैं, साथ ही एक उदाहरण भी दिखा सकते हैं कि इसे कैसे निष्पादित किया जाए।

तीन-तरफ़ा एनोवा का उपयोग कब करें

यहां कुछ परिदृश्य दिए गए हैं जिनमें आप तीन-तरफा एनोवा का उपयोग कर सकते हैं:

परिदृश्य 1: वनस्पति विज्ञान

एक वनस्पतिशास्त्री यह निर्धारित करना चाह सकता है कि (1) सूर्य का संपर्क, (2) पानी देने की आवृत्ति, और (3) उर्वरक का प्रकार पौधों की वृद्धि को कैसे प्रभावित करता है।

इस परिदृश्य में, वह तीन-तरफा एनोवा का प्रदर्शन कर सकती है क्योंकि तीन कारक और एक प्रतिक्रिया चर हैं।

परिदृश्य 2: खुदरा

एक खुदरा स्टोर का प्रबंधक यह निर्धारित करना चाह सकता है कि (1) सप्ताह का दिन, (2) स्टोर स्थान, और (3) विज्ञापन अभियान कुल बिक्री को कैसे प्रभावित करते हैं।

इस परिदृश्य में, वह तीन-तरफा एनोवा का प्रदर्शन कर सकता है क्योंकि तीन कारक और एक प्रतिक्रिया चर हैं।

परिदृश्य 3: चिकित्सा

एक डॉक्टर यह निर्धारित करना चाह सकता है कि (1) लिंग, (2) आहार, और (3) व्यायाम की आदतें वजन को कैसे प्रभावित करती हैं।

इस परिदृश्य में, वह तीन-तरफा एनोवा का प्रदर्शन कर सकती है क्योंकि तीन कारक और एक प्रतिक्रिया चर हैं।

थ्री-वे एनोवा: उदाहरण

मान लीजिए कि एक शोधकर्ता यह निर्धारित करना चाहता है कि क्या प्रशिक्षण कार्यक्रम, लिंग और खेल विभाजन कूद की ऊँचाई को प्रभावित करते हैं।

इसका परीक्षण करने के लिए, वह निम्नलिखित कारकों के साथ तीन-तरफ़ा एनोवा का प्रदर्शन कर सकता है:

• 1. प्रशिक्षण कार्यक्रम (कार्यक्रम 1 बनाम कार्यक्रम 2)
• 2. लिंग (पुरुष या महिला)
• 3. खेल प्रभाग (डिवीजन I बनाम डिवीजन II)

एकमात्र प्रतिक्रिया चर छलांग की ऊँचाई होगी।

मान लीजिए कि वह 40 लोगों पर यह डेटा एकत्र करता है:

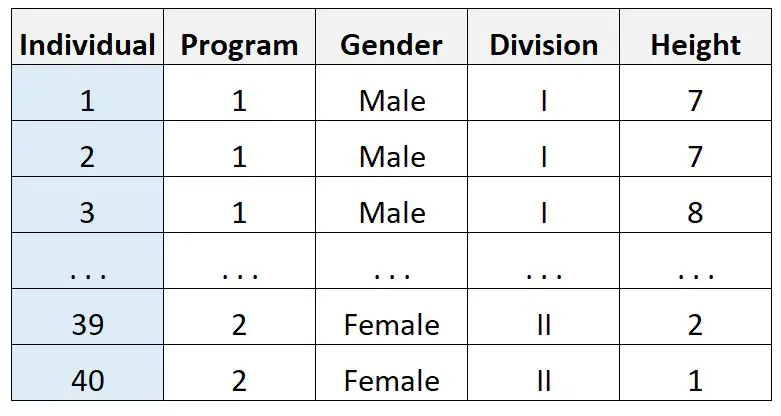
फिर वह तीन-तरफ़ा एनोवा निष्पादित करने के लिए सांख्यिकीय सॉफ़्टवेयर का उपयोग करता है और निम्नलिखित परिणाम प्राप्त करता है:

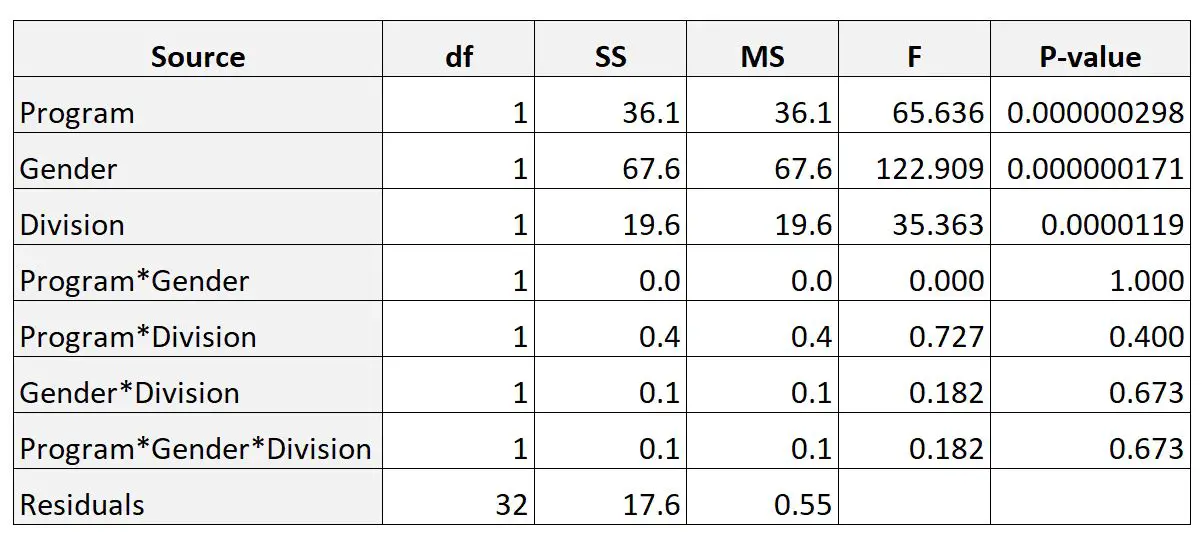
पी-वैल्यू कॉलम प्रत्येक व्यक्तिगत कारक के लिए पी-वैल्यू और कारकों के बीच बातचीत को प्रदर्शित करता है।

परिणामों से, हम देख सकते हैं कि तीन कारकों के बीच कोई भी इंटरैक्शन सांख्यिकीय रूप से महत्वपूर्ण नहीं था।

हम यह भी देख सकते हैं कि तीनों कारकों (कार्यक्रम, लिंग और प्रभाग) में से प्रत्येक सांख्यिकीय रूप से महत्वपूर्ण था।

अंत में, हम कहेंगे कि प्रशिक्षण कार्यक्रम, लिंग और विभाजन सभी खिलाड़ियों में बढ़ी हुई कूद ऊंचाई के महत्वपूर्ण संकेतक हैं।

हम यह भी कहेंगे कि इन तीन कारकों के बीच कोई महत्वपूर्ण परस्पर क्रिया प्रभाव नहीं है।

ध्यान दें : व्यवहार में, हम प्रत्येक कार्यक्रम, लिंग और प्रभाग के लिए औसत छलांग ऊंचाई की भी गणना करेंगे ताकि हम यह निर्धारित कर सकें कि प्रत्येक कारक का कौन सा स्तर कूद ऊंचाई में वृद्धि के साथ जुड़ा हुआ है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर और पायथन में तीन-तरफा एनोवा कैसे करें:

आर में तीन-तरफ़ा एनोवा कैसे निष्पादित करें
पायथन में थ्री-वे एनोवा कैसे निष्पादित करें