एक्सेल में त्रिकोणीय वितरण का उपयोग कैसे करें (उदाहरण के साथ)

त्रिकोणीय वितरण त्रिकोण के आकार के संभाव्यता घनत्व फ़ंक्शन के साथ एक सतत संभाव्यता वितरण है।

इसे तीन मानों द्वारा परिभाषित किया गया है:

• न्यूनतम मूल्य है
• अधिकतम मान बी
• अधिकतम मान सी

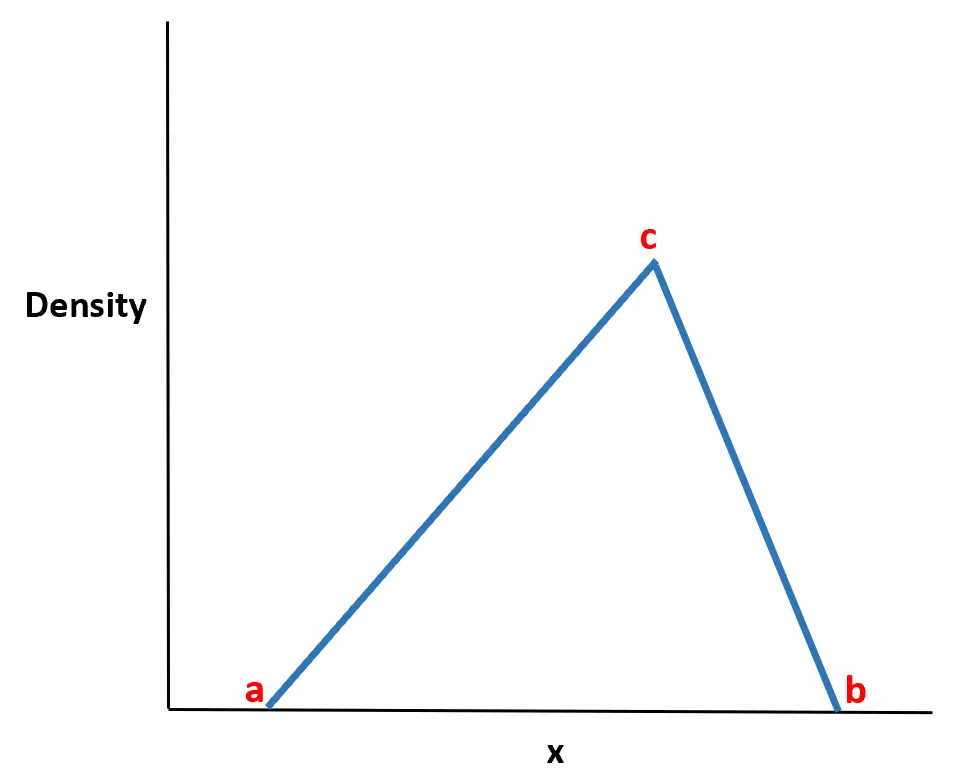
वितरण का नाम इस तथ्य से आता है कि संभाव्यता घनत्व फ़ंक्शन का आकार त्रिभुज जैसा होता है।

त्रिकोणीय वितरण में निम्नलिखित पीडीएफ और सीडीएफ हैं:

पीडीएफ:

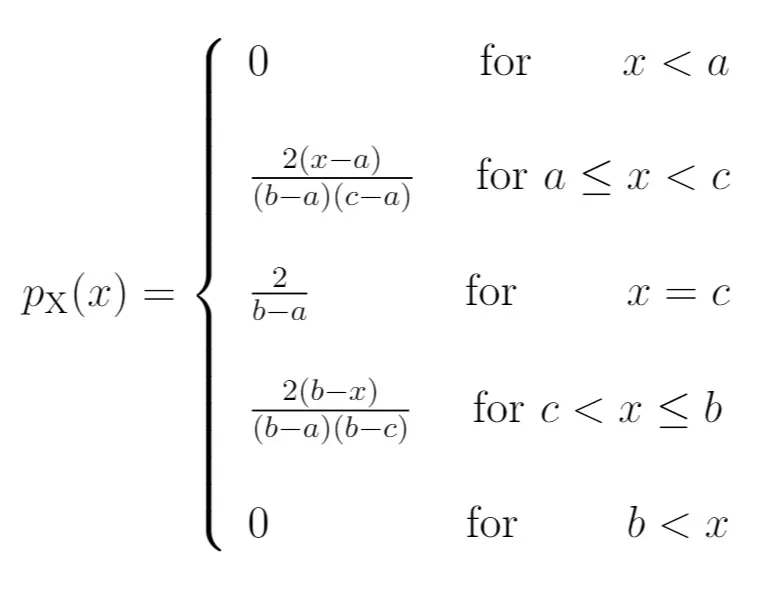
सीडीएफ:

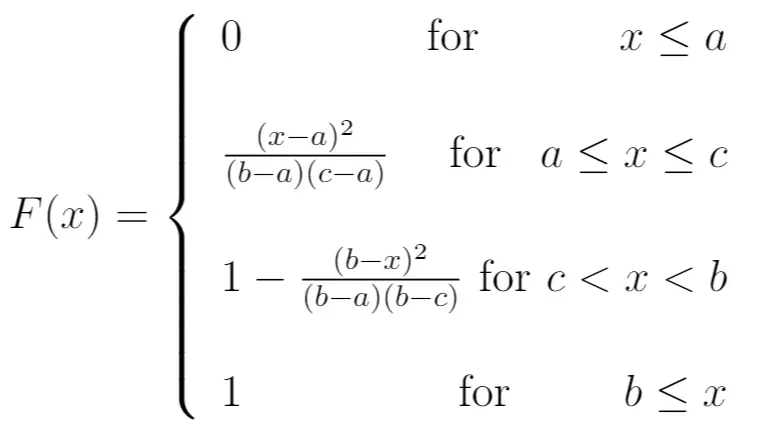
निम्नलिखित उदाहरण दिखाते हैं कि एक्सेल में संभावनाओं की गणना के लिए त्रिकोणीय वितरण का उपयोग कैसे करें।

उदाहरण 1: रेस्तरां बिक्री

मान लीजिए कि एक रेस्तरां का अनुमान है कि आने वाले सप्ताह के लिए उसकी कुल बिक्री न्यूनतम $10,000, अधिकतम $30,000 और संभवतः $25,000 होगी।

क्या संभावना है कि रेस्तरां की कुल बिक्री $20,000 से कम हो?

सीडीएफ के अनुसार, कुल बिक्री 20,000 डॉलर से कम होने की संभावना जानने के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

• पी(एक्स < एक्स) = (एक्सए) ² / ((बीए)(सीए))

एक्सेल में इस संभावना की गणना कैसे करें:

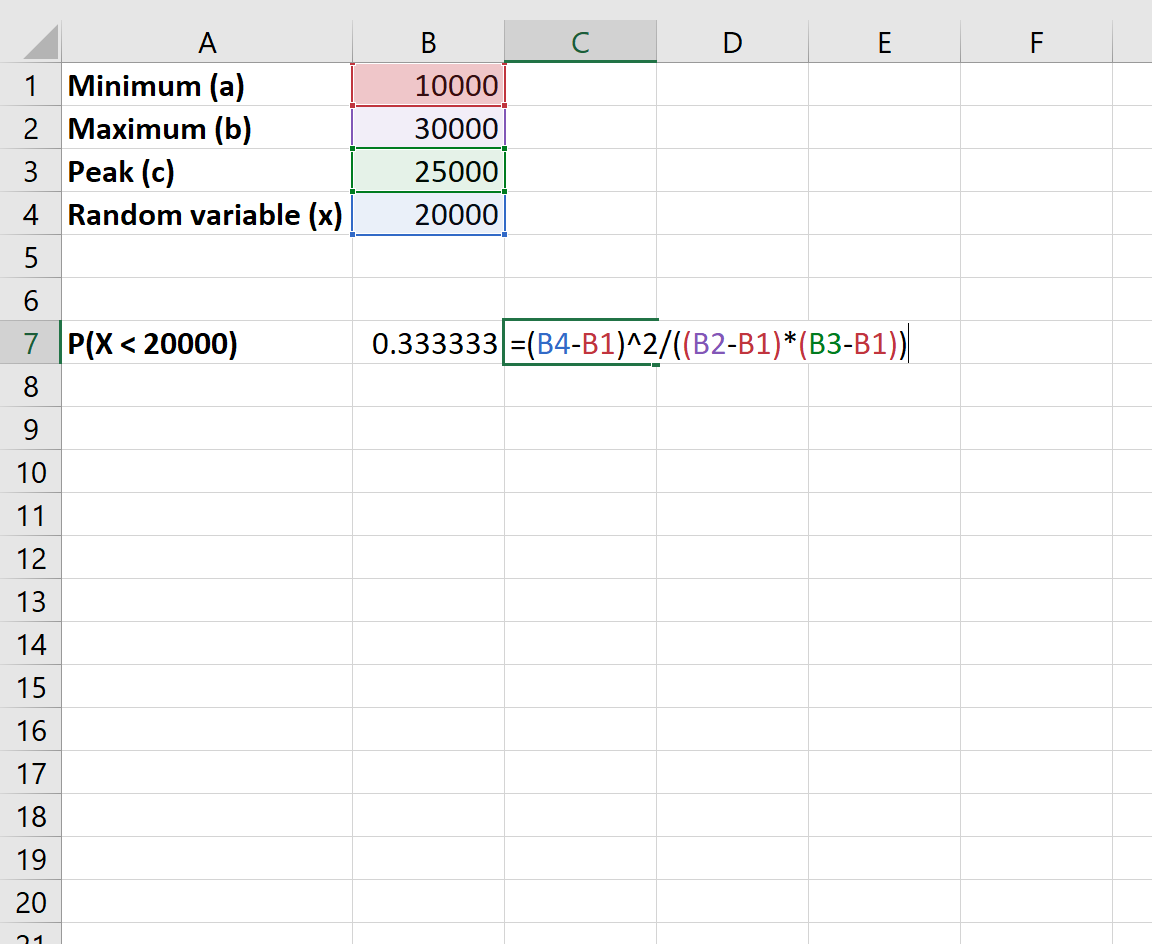
रेस्तरां की कुल बिक्री $20,000 से कम होने की संभावना 0.333 है।

उदाहरण 2: ग्राहकों की संख्या

मान लीजिए कि एक स्टोर का अनुमान है कि किसी दिए गए सप्ताह में आने वाले ग्राहकों की संख्या न्यूनतम 500, अधिकतम 2,000 और संभवतः 1,200 होगी।

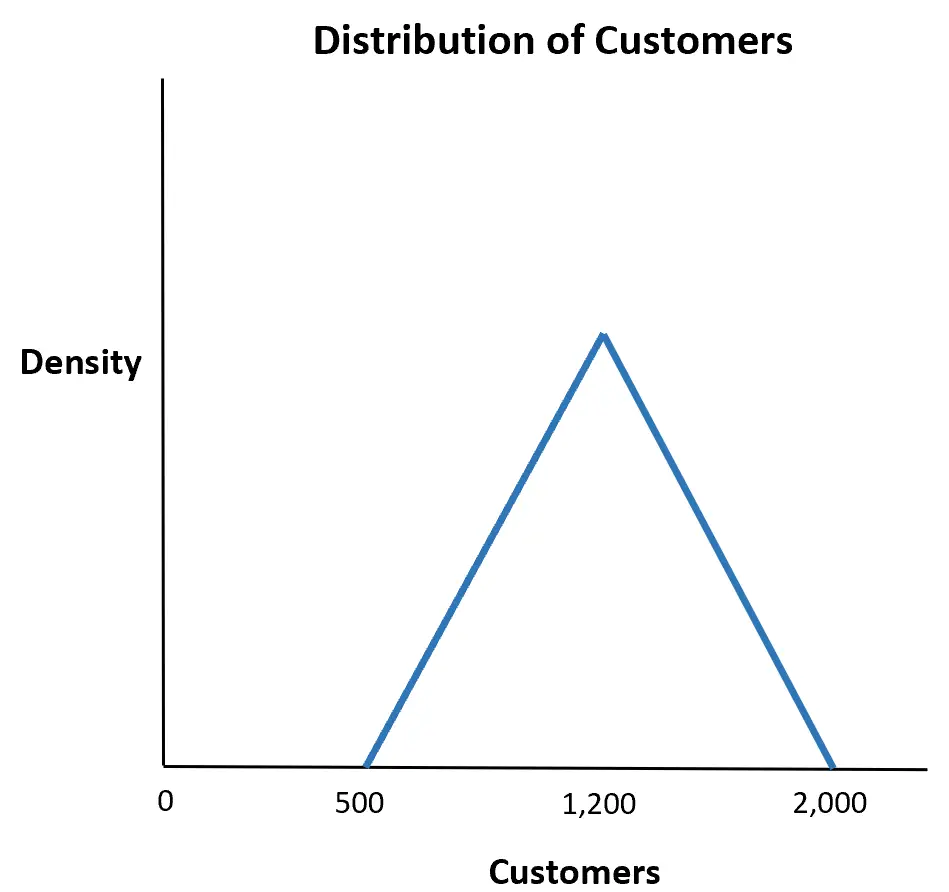
इसकी क्या संभावना है कि एक सप्ताह में 1,500 से अधिक ग्राहक स्टोर में प्रवेश करेंगे?

सीडीएफ के अनुसार, ग्राहकों की कुल संख्या 1,500 से अधिक होने की संभावना जानने के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

• पी(एक्स > एक्स) = 1 – [1 – (बीएक्स) ² / ((बीए)(बीसी))]

एक्सेल में इस संभावना की गणना कैसे करें:

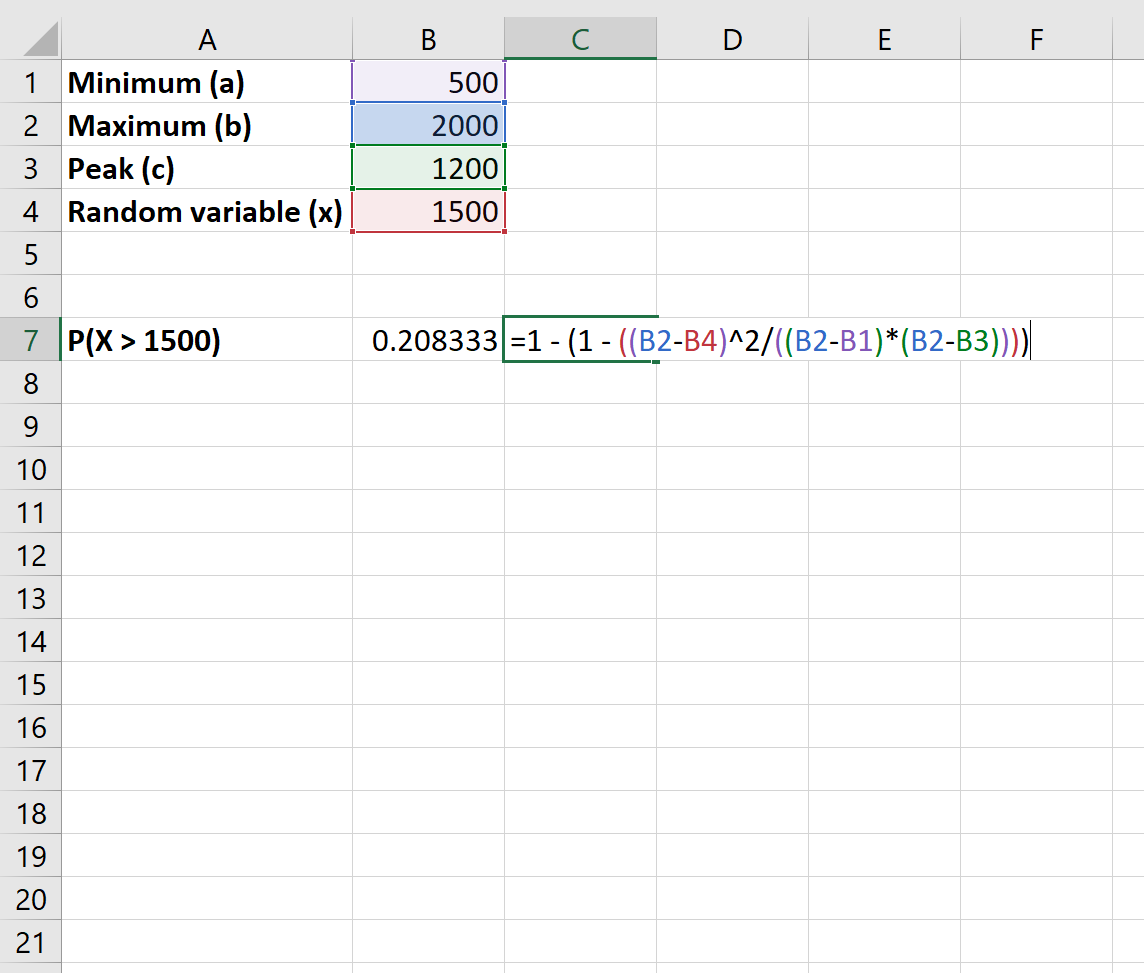
1,500 से अधिक ग्राहकों के स्टोर में प्रवेश करने की संभावना 0.208 है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल एक्सेल में अन्य संभाव्यता वितरणों का उपयोग करने का तरीका बताते हैं:

एक्सेल में द्विपद वितरण का उपयोग कैसे करें
एक्सेल में पॉइसन वितरण का उपयोग कैसे करें
Excel में समान वितरण का उपयोग कैसे करें