द्विपद वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में द्विपद वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसलिए आपको द्विपद वितरण की परिभाषा, द्विपद वितरण के उदाहरण और इस प्रकार के संभाव्यता वितरण के गुण मिलेंगे। इसके अतिरिक्त, आप ऑनलाइन कैलकुलेटर से द्विपद वितरण की किसी भी संभावना की गणना करने में सक्षम होंगे।

द्विपद वितरण क्या है?

द्विपद वितरण एक संभाव्यता वितरण है जो सफलता की निरंतर संभावना के साथ स्वतंत्र, द्विभाजित प्रयोगों की एक श्रृंखला निष्पादित करते समय सफलताओं की संख्या की गणना करता है।

दूसरे शब्दों में, द्विपद वितरण एक ऐसा वितरण है जो बर्नौली परीक्षणों के अनुक्रम के सफल परिणामों की संख्या का वर्णन करता है।

याद रखें कि बर्नौली परीक्षण एक ऐसा प्रयोग है जिसके दो संभावित परिणाम हैं: “सफलता” और “असफलता”। इसलिए, यदि “सफलता” की संभावना p है, तो “असफलता” की संभावना q=1-p है।

सामान्य तौर पर, किए गए प्रयोगों की कुल संख्या को पैरामीटर n से परिभाषित किया जाता है, जबकि p प्रत्येक प्रयोग की सफलता की संभावना है। इस प्रकार, एक यादृच्छिक चर जो द्विपद वितरण का अनुसरण करता है उसे इस प्रकार लिखा जाता है:

$X\sim\text{Bin}(n,p)$

ध्यान दें कि द्विपद वितरण में, एक ही प्रयोग को n बार दोहराया जाता है और प्रयोग एक दूसरे से स्वतंत्र होते हैं, इसलिए प्रत्येक प्रयोग की सफलता की संभावना समान होती है (पी) ।

द्विपद वितरण को द्विपद वितरण भी कहा जा सकता है।

द्विपद वितरण उदाहरण

एक बार जब हमने द्विपद वितरण की परिभाषा देख ली, तो हम अवधारणा को बेहतर ढंग से समझने के लिए इस प्रकार के वितरण का पालन करने वाले चर के कई उदाहरण देखेंगे।

एक सिक्के को 25 बार उछालने पर हेड आने की संख्या।
एक बास्केटबॉल खिलाड़ी द्वारा एक ही स्थान से टोकरी की ओर 60 बार शूट करने पर लिए गए शॉट्स की संख्या।
किसी पासे को 30 बार घुमाने पर हमें संख्या 6 प्राप्त होती है।
परीक्षा देने वाले कुल 50 छात्रों में से उत्तीर्ण होने वालों की संख्या।
100 उत्पादों के नमूने में दोषपूर्ण इकाइयों की संख्या.

द्विपद वितरण सूत्र

पैरामीटर x, n, p को देखते हुए, द्विपद वितरण की संभाव्यता फ़ंक्शन को x गुना p ^x गुना (1-p) ^nx में n की संयोजन संख्या के रूप में परिभाषित किया गया है।

इसलिए, द्विपद वितरण की संभावना की गणना करने का सूत्र है:

👉 आप द्विपद वितरण का अनुसरण करने वाले एक चर की संभावना की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

दूसरी ओर, द्विपद वितरण की संचयी संभावना की गणना प्रश्न में सफलता के मामलों की संख्या और पिछली सभी संभावनाओं को जोड़कर की जाती है। तो, द्विपद वितरण की संचयी संभावना की गणना करने का सूत्र है:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

द्विपद बंटन पर हल किया गया अभ्यास

हम एक सिक्के को 10 बार उछालते हैं, 6 चित आने की प्रायिकता क्या है?

इस समस्या में चर एक द्विपद वितरण का अनुसरण करता है क्योंकि सभी लॉन्च एक दूसरे से स्वतंत्र होते हैं और सफलता की संभावना भी समान होती है।

निस्संदेह, सफलता की संभावना 50% है, क्योंकि दो संभावित परिणामों में से केवल एक को ही सफलता माना जाता है।

$p=\cfrac{1}{2}=0,5$

इसलिए, इस अभ्यास का वितरण कुल 10 प्रयोगों और 0.5 की संभावना के साथ एक द्विपद है।

$X\sim\text{Bin}(10 ; 0,5)$

इसलिए, छह शीर्ष प्राप्त करने की संभावना निर्धारित करने के लिए, हमें द्विपद वितरण सूत्र को लागू करने की आवश्यकता है।

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

तो, एक सिक्के को दस बार उछालने पर ठीक छह चित आने की संभावना 20.51% है।

द्विपद बंटन की विशेषताएँ

द्विपद वितरण की निम्नलिखित विशेषताएं हैं:

द्विपद वितरण को दो मापदंडों के साथ परिभाषित किया गया है: n बर्नौली प्रयोगों की कुल संख्या है और दूसरी ओर, पी प्रत्येक बर्नौली प्रयोग की सफलता की संभावना है।

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

द्विपद वितरण का माध्य प्रत्येक प्रयोग की सफलता की संभावना से गुणा किए गए प्रयोगों की कुल संख्या के उत्पाद के बराबर है। इसलिए, द्विपद वितरण के माध्य की गणना करने के लिए, किसी को n को p से गुणा करना होगा।

$E[X]=n\cdot p$

द्विपद वितरण का विचरण सफलता की संभावना और विफलता की संभावना से गुणा किए गए परीक्षणों की कुल संख्या के बराबर होता है।

$Var(X)=n\cdot p\cdot (1-p)$

द्विपद वितरण के संभाव्यता फलन का सूत्र इस प्रकार है:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

इसी प्रकार, द्विपद वितरण के संचयी वितरण फलन का सूत्र है:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

समान प्रायिकता वाले दो स्वतंत्र द्विपद वितरणों का योग समान प्रायिकता मान p और n के साथ द्विपद वितरण के बराबर होता है, जो दोनों वितरणों के परीक्षणों की कुल संख्या का योग होता है।

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

बर्नौली वितरण द्विपद वितरण का एक विशेष मामला है जिसमें n=1 , यानी केवल एक प्रयोग किया जाता है।

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_यदि _X 1 , _X ₂ ,…, X _k ऐसे स्वतंत्र यादृच्छिक चर हैं

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

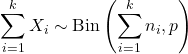
द्विपद वितरण कैलकुलेटर

संभाव्यता की गणना करने के लिए निम्नलिखित कैलकुलेटर में द्विपद वितरण के पैरामीटर पी, एन और एक्स के मान दर्ज करें। आपको उस संभावना का चयन करना होगा जिसकी आप गणना करना चाहते हैं और दशमलव विभाजक के रूप में बिंदु का उपयोग करके संख्याएं दर्ज करें, उदाहरण के लिए 0.1667।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने