पायथन में द्विपद वितरण का उपयोग कैसे करें

द्विपद वितरण सांख्यिकी में सबसे अधिक उपयोग किए जाने वाले वितरणों में से एक है। यह n द्विपद प्रयोगों में k सफलताएँ प्राप्त करने की संभावना का वर्णन करता है।

यदि एक यादृच्छिक चर X एक द्विपद वितरण का अनुसरण करता है, तो संभावना है कि X = k की सफलता निम्नलिखित सूत्र द्वारा पाई जा सकती है:

पी(एक्स=के) = _एन सी _के * पी ^के * (1-पी) ^एनके

सोना:

• n: परीक्षणों की संख्या
• k: सफलताओं की संख्या
• पी: किसी दिए गए परीक्षण पर सफलता की संभावना
• _n C _k : n परीक्षणों में k सफलताएँ प्राप्त करने के तरीकों की संख्या

यह ट्यूटोरियल बताता है कि पायथन में द्विपद वितरण का उपयोग कैसे करें।

द्विपद बंटन कैसे उत्पन्न करें

आप संख्यात्मक लाइब्रेरी के रैंडम.बिनोमियल फ़ंक्शन का उपयोग करके द्विपद वितरण का अनुसरण करने वाले मानों की एक सरणी उत्पन्न कर सकते हैं:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

परिणामी तालिका में प्रत्येक संख्या 10 परीक्षणों के दौरान मिली “सफलताओं” की संख्या को दर्शाती है, जहां किसी दिए गए परीक्षण में सफलता की संभावना 0.25 थी।

द्विपद वितरण का उपयोग करके संभावनाओं की गणना कैसे करें

आप scipy लाइब्रेरी के बिनोम फ़ंक्शन का उपयोग करके द्विपद संभाव्यता के बारे में प्रश्नों का उत्तर भी दे सकते हैं।

प्रश्न 1: नाथन अपने 60% फ़्री थ्रो प्रयास करता है। यदि वह 12 फ्री थ्रो करता है, तो इसकी क्या प्रायिकता है कि वह ठीक 10 बनाता है?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

नाथन द्वारा ठीक 10 फ्री थ्रो करने की प्रायिकता 0.0639 है।

प्रश्न 2: मार्टी एक सिक्के को 5 बार उछालता है। इसकी क्या प्रायिकता है कि सिक्का 2 बार या उससे कम बार शीर्ष पर आये?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

सिक्के के 2 बार या उससे कम बार शीर्ष पर आने की प्रायिकता 0.5 है।

प्रश्न 3: हम जानते हैं कि 70% व्यक्ति एक निश्चित कानून का समर्थन करते हैं। यदि 10 व्यक्तियों को यादृच्छिक रूप से चुना जाता है, तो क्या संभावना है कि उनमें से 4 और 6 के बीच कानून का समर्थन करते हैं?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

4 और 6 के बीच यादृच्छिक रूप से चुने गए व्यक्तियों के कानून का समर्थन करने की संभावना 0.3398 है।

द्विपद वितरण की कल्पना कैसे करें

आप सीबॉर्न और मैटप्लोटलिब लाइब्रेरी का उपयोग करके पायथन में एक द्विपद वितरण की कल्पना कर सकते हैं:

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

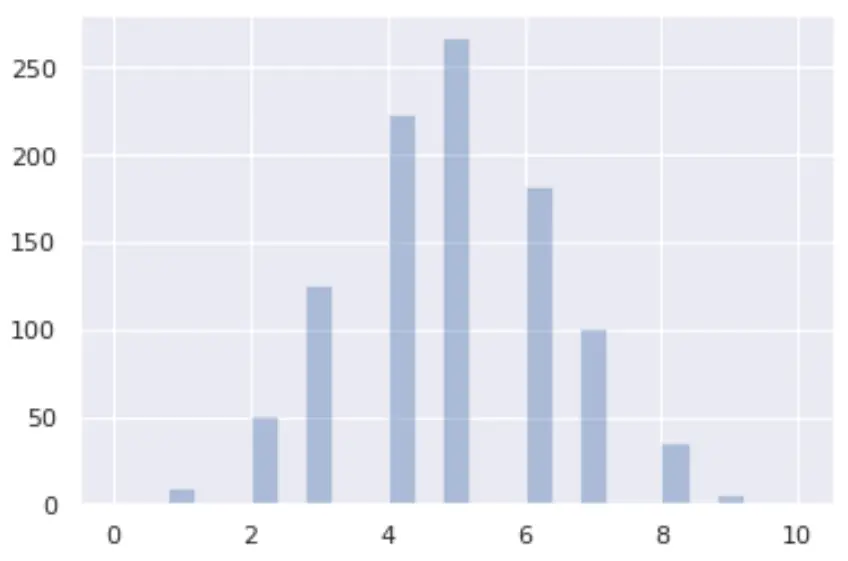
चाय