नमूने का वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में नमूनाकरण वितरण क्या है और इसका उपयोग किस लिए किया जाता है। तो आपको नमूना वितरण का अर्थ, नमूना वितरण का एक ठोस उदाहरण और, इसके अलावा, सबसे सामान्य प्रकार के नमूना वितरण के सूत्र मिलेंगे।

नमूना वितरण क्या है?

नमूना वितरण , या नमूना वितरण , वह वितरण है जो किसी जनसंख्या के सभी संभावित नमूनों पर विचार करने के परिणामस्वरूप होता है। दूसरे शब्दों में, नमूना वितरण एक जनसंख्या से सभी संभावित नमूनों के नमूना पैरामीटर की गणना करके प्राप्त वितरण है।

उदाहरण के लिए, यदि हम एक सांख्यिकीय आबादी से सभी संभावित नमूने निकालते हैं और प्रत्येक नमूने के माध्य की गणना करते हैं, तो नमूना साधनों का सेट एक नमूना वितरण बनाता है। अधिक सटीक रूप से, चूंकि परिकलित पैरामीटर अंकगणितीय माध्य है, यह माध्य का नमूना वितरण है।

आंकड़ों में, नमूना वितरण का उपयोग एकल नमूने का अध्ययन करते समय जनसंख्या पैरामीटर के मूल्य के करीब पहुंचने की संभावना की गणना करने के लिए किया जाता है। इसी प्रकार, नमूना वितरण हमें किसी दिए गए नमूना आकार के लिए नमूना त्रुटि का अनुमान लगाने की अनुमति देता है।

नमूना वितरण का उदाहरण

अब जब हम नमूना वितरण की परिभाषा जानते हैं, तो आइए अवधारणा को पूरी तरह से समझने के लिए एक सरल उदाहरण देखें।

एक बॉक्स में हमने तीन गेंदें रखीं और प्रत्येक पर एक से तीन तक एक नंबर लिखा था, ताकि एक गेंद पर नंबर 1 हो, दूसरी गेंद पर नंबर 2 हो और आखिरी गेंद पर नंबर 3 हो। आकार के नमूने के लिए n = 2, यदि प्रतिस्थापन वाले नमूने चुने जाते हैं तो माध्य के नमूना वितरण की संभावनाओं की गणना करता है।

नमूनों को प्रतिस्थापन के साथ चुना जाता है, अर्थात, नमूने के पहले तत्व का चयन करने के लिए उठाई गई गेंद बॉक्स में वापस आ जाती है और दूसरे निष्कर्षण के दौरान फिर से चुना जा सकता है। इसलिए, जनसंख्या से सभी संभावित नमूने हैं:

1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3

इस प्रकार, हम प्रत्येक संभावित नमूने के अंकगणितीय माध्य की गणना करते हैं:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

इसलिए, जनसंख्या से यादृच्छिक नमूना चुनते समय नमूना माध्य के प्रत्येक मान को प्राप्त करने की संभावनाएं इस प्रकार हैं:

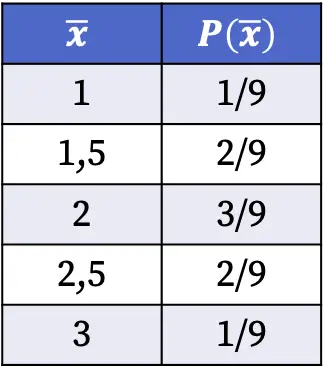
उपरोक्त तालिका में दिखाए गए नमूना वितरण की संभावनाओं की गणना संभावित मामलों की कुल संख्या से उक्त औसत मूल्य वाले नमूनों की संख्या को विभाजित करके की गई थी। उदाहरण के लिए: संभावित नौ में से दो मामलों में नमूना माध्य 1.5 है, इसलिए P(1.5)=2/9।

नमूनाकरण वितरण के प्रकार

नमूना वितरण (या नमूना वितरण) को नमूना पैरामीटर के आधार पर वर्गीकृत किया जा सकता है जिससे वे प्राप्त किए गए थे। तो, सबसे सामान्य प्रकार के वितरण इस प्रकार हैं:

माध्य का नमूना वितरण : यह नमूना वितरण है जो प्रत्येक नमूने के अंकगणितीय माध्य की गणना के परिणामस्वरूप होता है।
आनुपातिक नमूना वितरण : यह सभी नमूनों के अनुपात की गणना करके प्राप्त किया गया नमूना वितरण है।
प्रसरण का नमूना वितरण : यह नमूना वितरण है जो नमूने में सभी प्रसरणों का सेट बनाता है।
साधन नमूना वितरण का अंतर : वह नमूना वितरण है जो दो अलग-अलग आबादी के सभी संभावित नमूनों के साधनों के बीच अंतर की गणना के परिणामस्वरूप होता है।
अनुपात नमूना वितरण में अंतर : दो आबादी से सभी संभावित नमूना अनुपात घटाकर प्राप्त नमूना वितरण है।

प्रत्येक प्रकार के नमूना वितरण को नीचे अधिक विस्तार से समझाया गया है।

माध्य का नमूना वितरण

एक ऐसी जनसंख्या को देखते हुए जो माध्य के साथ सामान्य संभाव्यता वितरण का अनुसरण करती है

$\mu$

और मानक विचलन

$\sigma$

और आकार के नमूने निकाले जाते हैं

$n$

, माध्य का नमूना वितरण भी निम्नलिखित विशेषताओं वाले सामान्य वितरण द्वारा परिभाषित किया जाएगा:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

सोना

$\mu_{\overline{x}}$

माध्य के नमूना वितरण का माध्य है और

$\sigma_{\overline{x}}$

इसका मानक विचलन है. आगे,

$\cfrac{\sigma}{\sqrt{n}}$

नमूना वितरण की मानक त्रुटि है।

नोट: यदि जनसंख्या सामान्य वितरण का पालन नहीं करती है, लेकिन नमूना आकार बड़ा है (n>30), तो माध्य का नमूना वितरण भी केंद्रीय प्रमेय सीमा द्वारा उपरोक्त सामान्य वितरण के बराबर अनुमानित किया जा सकता है।

इसलिए, चूंकि माध्य का नमूना वितरण सामान्य वितरण का अनुसरण करता है, नमूना माध्य से संबंधित किसी भी संभावना की गणना करने का सूत्र है:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

सोना:

$\overline{x}$

नमूना साधन है.
$\mu$

यह जनसंख्या का औसत है.
$s$

जनसंख्या मानक विचलन है.
$n$

नमूना आकार है.
$Z$

मानक सामान्य वितरण N(0,1) द्वारा परिभाषित एक चर है।

➤ देखें: माध्य के नमूना वितरण पर हल किया गया अभ्यास

अनुपात का नमूना वितरण

वास्तव में, जब हम किसी नमूने के अनुपात का अध्ययन करते हैं, तो हम सफलता के मामलों का विश्लेषण करते हैं। इसलिए, अध्ययन में यादृच्छिक चर एक द्विपद संभाव्यता वितरण का अनुसरण करता है।

केंद्रीय सीमा प्रमेय के अनुसार, बड़े आकार (n>30) के लिए हम एक द्विपद वितरण को सामान्य वितरण के करीब ला सकते हैं। इसलिए, अनुपात का नमूना वितरण निम्नलिखित मापदंडों के साथ एक सामान्य वितरण का अनुमान लगाता है:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

सोना

$p$

सफलता की संभावना है और

$q$

विफलता की संभावना है

$q=1-p$

नोट: एक द्विपद वितरण को केवल सामान्य वितरण के समान ही अनुमानित किया जा सकता है यदि

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

और

$nq\ge 5$

इसलिए, चूंकि अनुपात के नमूना वितरण को सामान्य वितरण के बराबर अनुमानित किया जा सकता है, इसलिए नमूने के अनुपात से संबंधित किसी भी संभावना की गणना करने का सूत्र है:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

सोना:

$\widehat{p}$

नमूना अनुपात है.
$p$

जनसंख्या का अनुपात है.
$q$

जनसंख्या की विफलता की संभावना है,

$q=1-p$

.
$n$

नमूना आकार है.
$Z$

मानक सामान्य वितरण N(0,1) द्वारा परिभाषित एक चर है।

➤ देखें: अनुपात के नमूना वितरण पर हल किया गया अभ्यास

भिन्नता का नमूना वितरण

विचरण का नमूना वितरण ची-स्क्वायर संभाव्यता वितरण द्वारा परिभाषित किया गया है। इसलिए, विचरण के नमूना वितरण के आँकड़ों का सूत्र है:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

सोना:

$\chi^2$

विचरण के नमूना वितरण का आँकड़ा है, जो ची-स्क्वायर वितरण का अनुसरण करता है।
$n$

नमूना आकार है.
$s^2$

नमूना विचरण है.
$\sigma^2$

जनसंख्या विचरण है.

➤ देखें: विचरण के नमूना वितरण पर हल किया गया अभ्यास

साधनों के अंतर का नमूना वितरण

यदि नमूना आकार काफी बड़ा है (n ₁ ≥30 और n ₂ ≥30), तो माध्य अंतर का नमूना वितरण सामान्य वितरण का अनुसरण करता है। अधिक सटीक रूप से, उक्त वितरण के मापदंडों की गणना निम्नानुसार की जाती है:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

नोट: यदि दोनों आबादी सामान्य वितरण हैं, तो साधनों में अंतर का नमूना वितरण नमूना आकार की परवाह किए बिना सामान्य वितरण का अनुसरण करता है।

इसलिए, चूंकि साधनों में अंतर का नमूना वितरण सामान्य वितरण द्वारा परिभाषित किया गया है, इसलिए साधनों में अंतर के नमूना वितरण के आंकड़ों की गणना करने का सूत्र है:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

सोना:

$\overline{x_i}$

नमूना I का माध्य है.
$\mu_i$

जनसंख्या का माध्य है I
$\sigma_i$

जनसंख्या का मानक विचलन है I
$n_i$

नमूना आकार है I
$Z$

मानक सामान्य वितरण N(0,1) द्वारा परिभाषित एक चर है।

ध्यान दें कि अलग-अलग आबादी के नमूनों में अलग-अलग नमूना आकार हो सकते हैं।

➤ देखें: साधनों के अंतर के नमूना वितरण पर हल किया गया अभ्यास

अनुपातों में अंतर का नमूना वितरण

अनुपात नमूना वितरण में अंतर के लिए चुने गए नमूनों को द्विपद वितरण द्वारा परिभाषित किया गया है, क्योंकि व्यावहारिक उद्देश्यों के लिए अनुपात सफलता के मामलों का अवलोकनों की कुल संख्या का अनुपात है।

हालाँकि, केंद्रीय सीमा प्रमेय के कारण, द्विपद वितरण को सामान्य संभाव्यता वितरण के बराबर अनुमानित किया जा सकता है। इसलिए, अनुपात में अंतर के नमूना वितरण को निम्नलिखित विशेषताओं के साथ सामान्य वितरण के रूप में अनुमानित किया जा सकता है:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

ध्यान दें: अनुपात में अंतर का नमूना वितरण केवल सामान्य वितरण के लिए अनुमानित किया जा सकता है यदि

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

और

$n_2q_2\geq5$

इसलिए, चूंकि अनुपातों में अंतर के नमूना वितरण को सामान्य वितरण के बराबर अनुमानित किया जा सकता है, अनुपातों में अंतर के नमूना वितरण के आंकड़ों की गणना करने का सूत्र इस प्रकार है:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

सोना:

$\widehat{p_i}$

नमूना अनुपात है I
$p_i$

जनसंख्या का अनुपात है i.
$q_i$

जनसंख्या की विफलता की संभावना है I,

$q_i=1-p_i$

.
$n_i$

नमूना आकार है I
$Z$

मानक सामान्य वितरण N(0,1) द्वारा परिभाषित एक चर है।

➤ देखें: अनुपातों के अंतर के नमूना वितरण पर हल किया गया अभ्यास

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

नमूना वितरण क्या है?

नमूना वितरण का उदाहरण

नमूनाकरण वितरण के प्रकार

माध्य का नमूना वितरण

अनुपात का नमूना वितरण

भिन्नता का नमूना वितरण

साधनों के अंतर का नमूना वितरण

अनुपातों में अंतर का नमूना वितरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने