एक नीरस रिश्ता क्या है? (परिभाषा + उदाहरण)

आंकड़ों में, दो चर के बीच एक मोनोटोनिक संबंध एक ऐसे परिदृश्य को संदर्भित करता है जिसमें एक चर में परिवर्तन आमतौर पर दूसरे चर में एक विशिष्ट दिशा में परिवर्तन के साथ जुड़ा होता है।

एकरस संबंध दो प्रकार के होते हैं:

सकारात्मक मोनोटोनिक: जब एक चर का मान बढ़ता है, तो दूसरे चर का मान भी बढ़ने लगता है।

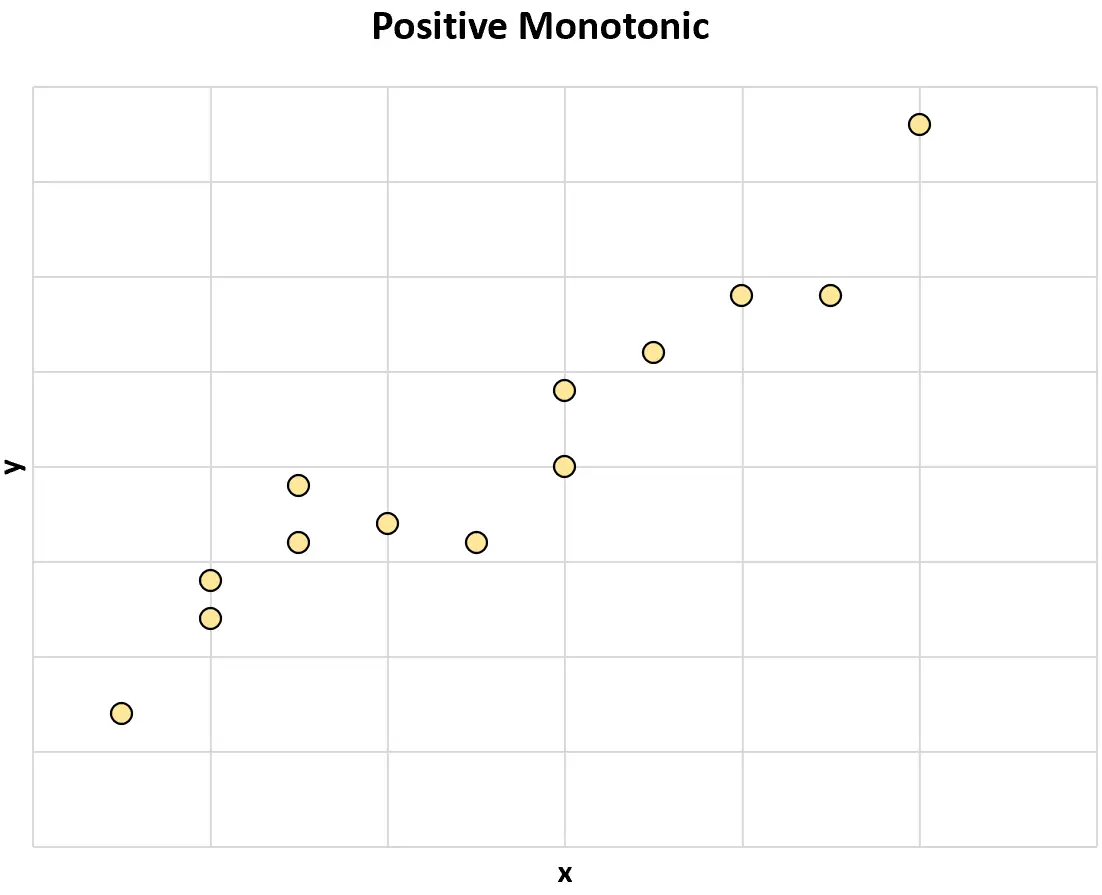
नकारात्मक मोनोटोनिक: जब एक चर का मान बढ़ता है, तो दूसरे चर का मान घटने लगता है।

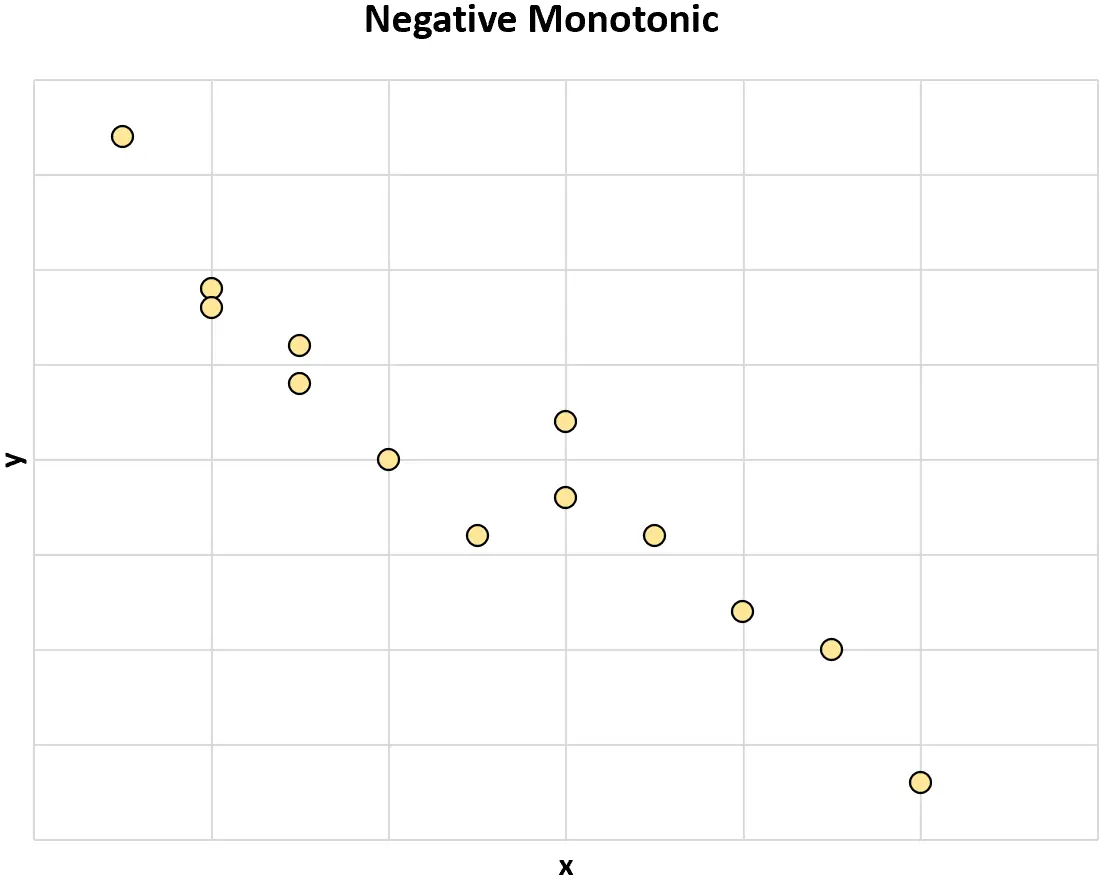
यदि दो चर आम तौर पर एक ही दिशा में नहीं बदलते हैं, तो उन्हें गैर-मोनोटोनिक संबंध कहा जाता है।

यहां दो चरों के बीच गैर-मोनोटोनिक संबंध का एक उदाहरण दिया गया है:

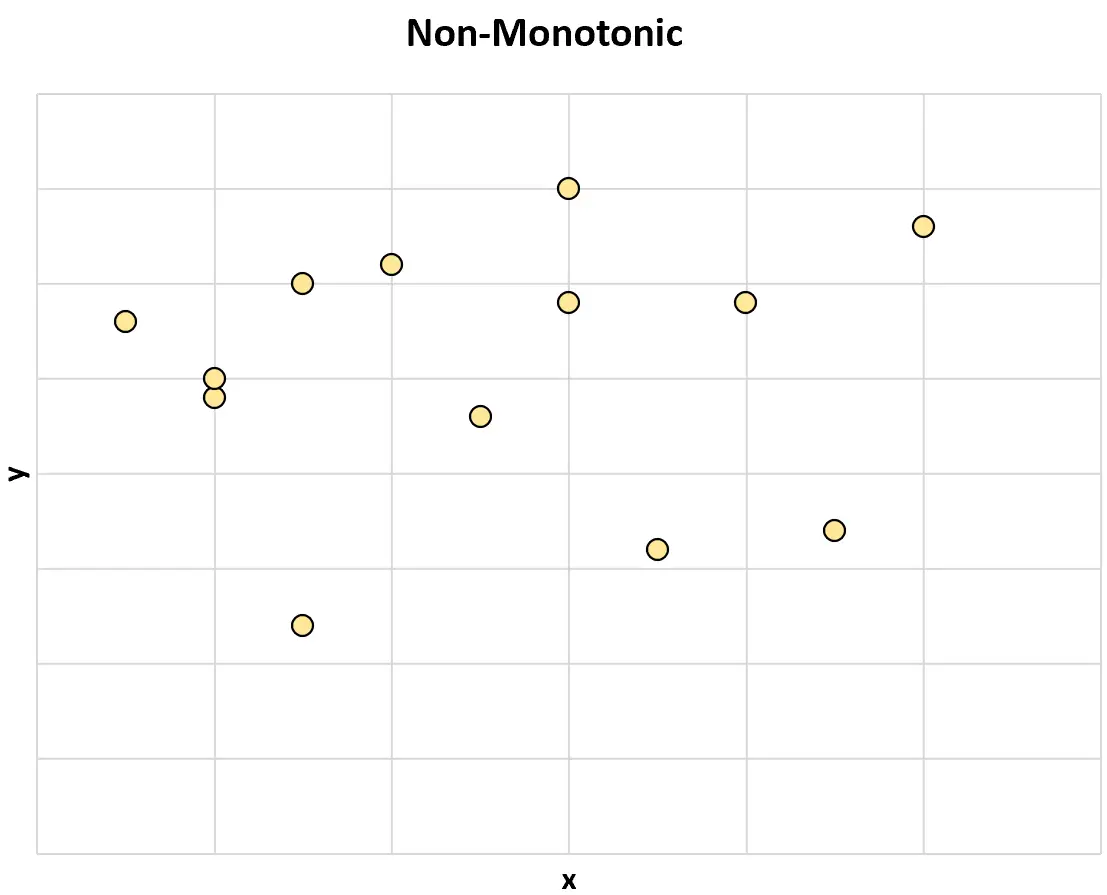
और यहां दो चरों के बीच गैर-मोनोटोनिक संबंध का एक और उदाहरण है:

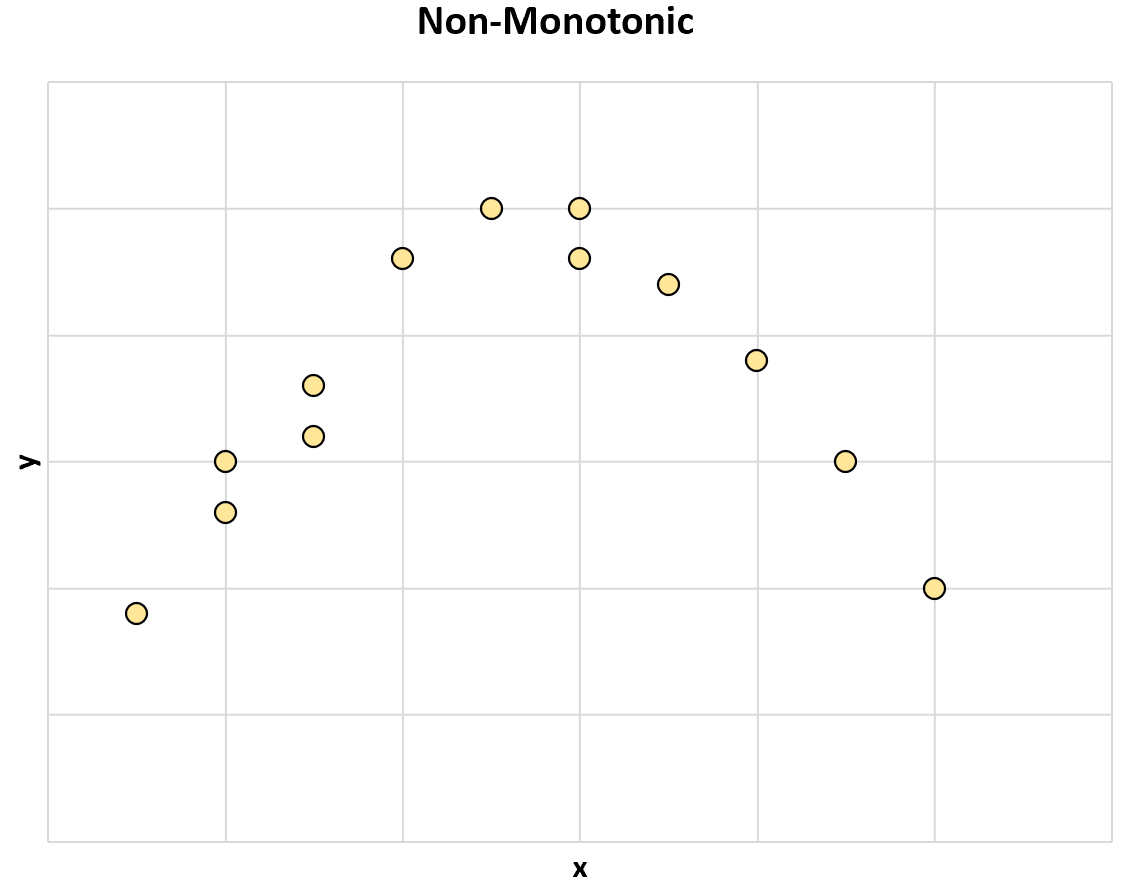
जैसे-जैसे x का मान बढ़ता है, कभी-कभी y का मान बढ़ता है, लेकिन कभी-कभी y का मान घट जाता है ।

पूरी तरह से नीरस या पूरी तरह से नीरस नहीं

कहा जाता है कि दो चरों में सख्ती से एकरस संबंध होता है यदि एक चर में परिवर्तन हमेशा दूसरे चर में उसी दिशा में परिवर्तन से जुड़ा होता है।

उदाहरण के लिए, निम्नलिखित ग्राफ़ दो चरों के बीच एक सख्ती से सकारात्मक मोनोटोनिक संबंध दिखाता है:

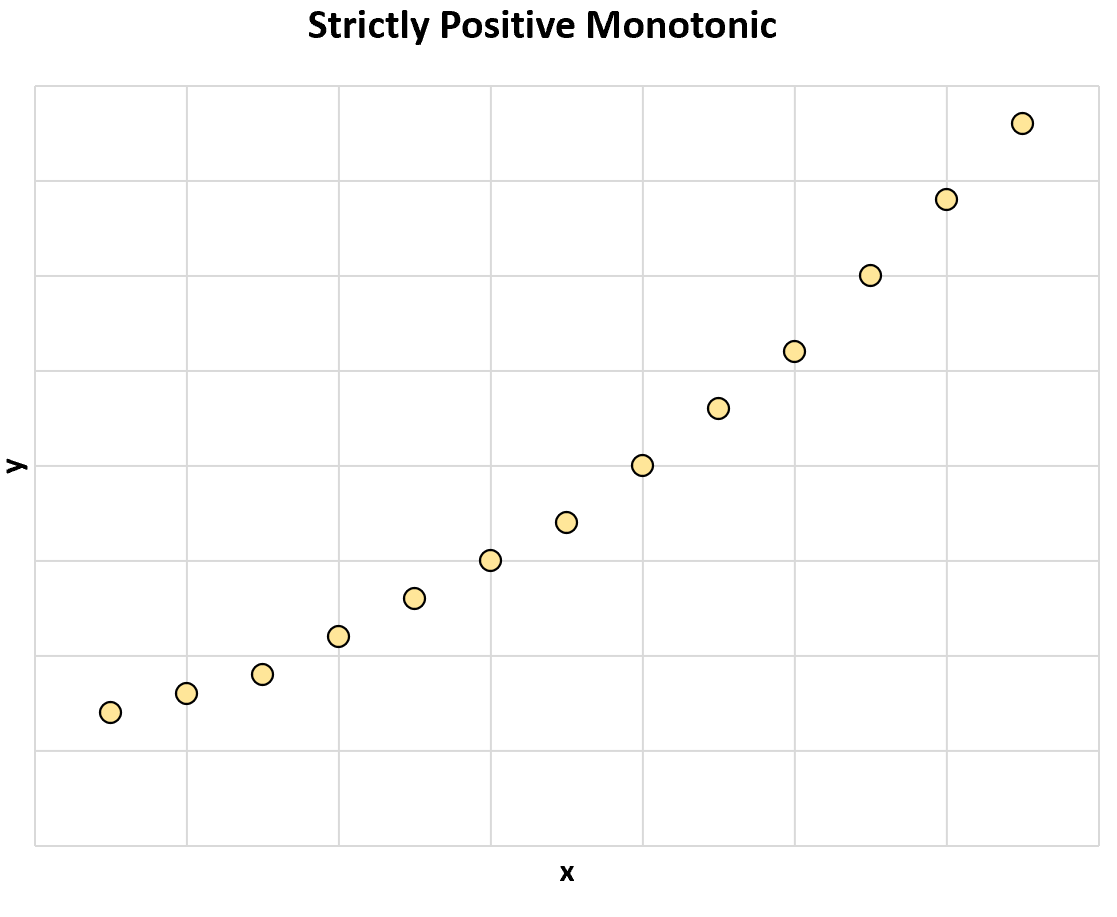
जैसे-जैसे x का मान बढ़ता है, y का मान सदैव बढ़ता जाता है।

निम्नलिखित ग्राफ़ दो चरों के बीच एक सख्ती से नकारात्मक मोनोटोनिक संबंध दिखाता है:

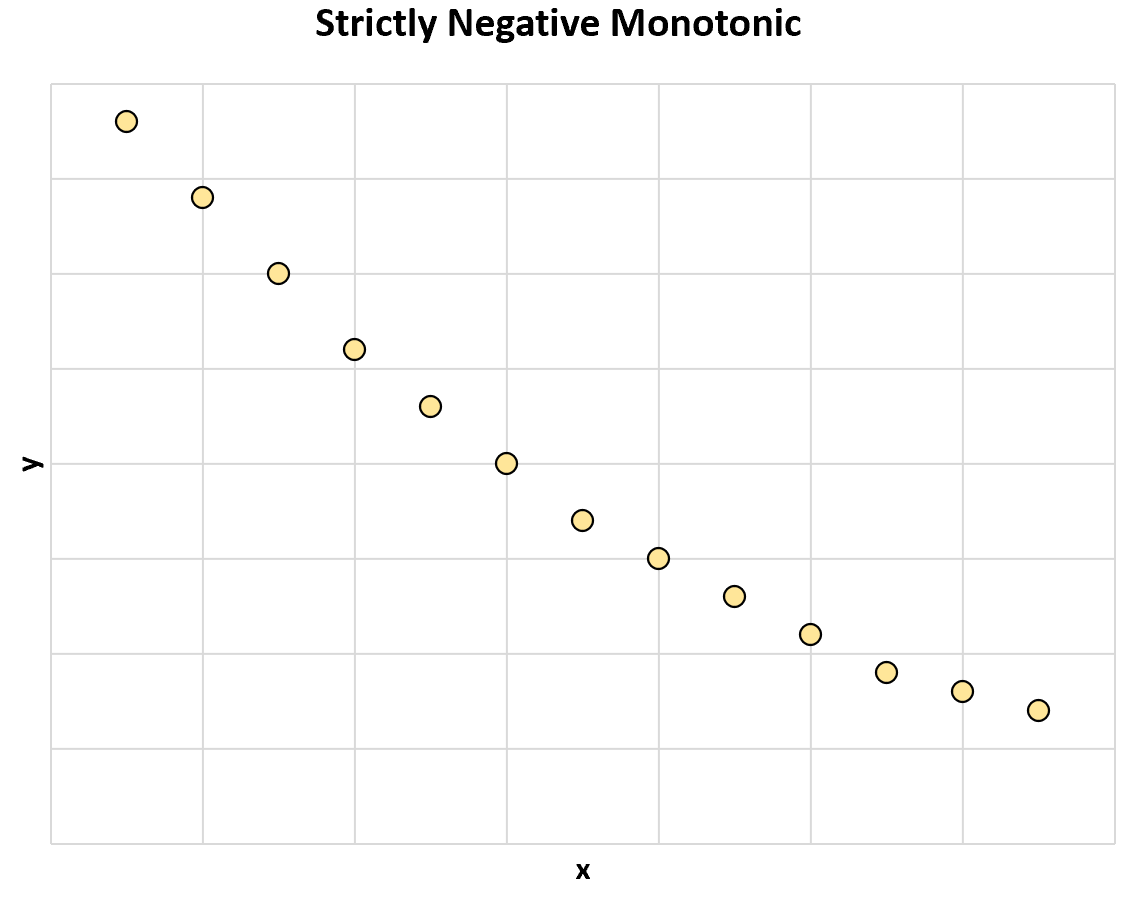
जैसे-जैसे x का मान बढ़ता है, y का मान सदैव घटता जाता है।

एकरस संबंधों को कैसे मापें?

दो चरों के बीच संबंध को मापने का सबसे आम तरीका पियर्सन सहसंबंध गुणांक का उपयोग करना है, जो दो चरों के बीच रैखिक संबंध को मापता है।

यह गुणांक हमेशा -1 और 1 के बीच मान लेता है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

गुणांक 1 के जितना करीब होगा, दो चरों के बीच सकारात्मक संबंध उतना ही मजबूत होगा। इसके विपरीत, गुणांक -1 के जितना करीब होगा, दो चर के बीच नकारात्मक संबंध उतना ही मजबूत होगा।

हालाँकि, यदि दो चर के बीच का संबंध मोनोटोनिक लेकिन गैर-रैखिक (एक घातीय संबंध की तरह) है, तो स्पीयरमैन रैंक सहसंबंध का उपयोग करना एक अच्छा विचार है, जिसे मोनोटोनिक संबंधों को अच्छी तरह से संभालने के लिए डिज़ाइन किया गया था।

भले ही आप किस प्रकार के सहसंबंध गुणांक की गणना कर रहे हों, चरों के बीच संबंध की कल्पना करने के लिए एक स्कैटरप्लॉट बनाना हमेशा एक अच्छा विचार है।