पायथन में कोवरियन्स मैट्रिक्स कैसे बनाएं

सहप्रसरण इस बात का माप है कि एक चर में परिवर्तन दूसरे चर में परिवर्तन से कैसे जुड़े हैं। अधिक विशेष रूप से, यह उस डिग्री का माप है जिससे दो चर रैखिक रूप से जुड़े हुए हैं।

सहप्रसरण मैट्रिक्स एक वर्ग मैट्रिक्स है जो कई अलग-अलग चरों के बीच सहप्रसरण को दर्शाता है। यह समझने का एक उपयोगी तरीका हो सकता है कि डेटा सेट में विभिन्न चर कैसे संबंधित हैं।

निम्नलिखित उदाहरण दिखाता है कि पायथन में सहप्रसरण मैट्रिक्स कैसे बनाया जाए।

पायथन में कोवरियन्स मैट्रिक्स कैसे बनाएं

पायथन में सहप्रसरण मैट्रिक्स बनाने के लिए निम्नलिखित चरणों का उपयोग करें।

चरण 1: डेटासेट बनाएं।

सबसे पहले, हम एक डेटासेट बनाएंगे जिसमें तीन विषयों: गणित, विज्ञान और इतिहास में 10 अलग-अलग छात्रों के परीक्षण स्कोर शामिल होंगे।

 import numpy as np

math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95]
science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94]
history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78]

data = np.array([math, science, history])

चरण 2: सहप्रसरण मैट्रिक्स बनाएं।

इसके बाद, हम numpy cov() फ़ंक्शन का उपयोग करके इस डेटासेट के लिए सहप्रसरण मैट्रिक्स बनाएंगे, जिसमें पूर्वाग्रह = सत्य निर्दिष्ट किया जाएगा ताकि हम जनसंख्या सहप्रसरण मैट्रिक्स की गणना कर सकें।

 np.cov(data, bias= True )

array([[ 64.96, 33.2, -24.44],
       [33.2, 56.4, -24.1],
       [-24.44, -24.1, 75.56]])

चरण 3: सहप्रसरण मैट्रिक्स की व्याख्या करें।

मैट्रिक्स के विकर्णों के मान केवल प्रत्येक विषय के प्रसरण हैं। उदाहरण के लिए:

• गणित के अंकों का प्रसरण 64.96 है
• विज्ञान के अंकों का अंतर 56.4 है
• ऐतिहासिक स्कोर भिन्नता 75.56 है

मैट्रिक्स के अन्य मान विभिन्न विषयों के बीच सहप्रसरण का प्रतिनिधित्व करते हैं। उदाहरण के लिए:

• गणित और विज्ञान के अंकों के बीच अंतर 33.2 है।
• गणित और इतिहास के अंकों के बीच सहप्रसरण -24.44 है।
• विज्ञान और इतिहास के अंकों के बीच सहप्रसरण -24.1 है।

सहप्रसरण के लिए एक सकारात्मक संख्या इंगित करती है कि दो चर एक साथ बढ़ने या घटने की प्रवृत्ति रखते हैं। उदाहरण के लिए, गणित और विज्ञान में एक सकारात्मक सहप्रसरण (33.2) है, जो दर्शाता है कि जो छात्र गणित में उच्च अंक प्राप्त करते हैं, वे विज्ञान में भी उच्च अंक प्राप्त करते हैं। इसके विपरीत, जो छात्र गणित में खराब प्रदर्शन करते हैं, वे विज्ञान में भी खराब प्रदर्शन करते हैं।

सहप्रसरण के लिए एक ऋणात्मक संख्या इंगित करती है कि जैसे-जैसे एक चर बढ़ता है, दूसरा चर घटता जाता है। उदाहरण के लिए, गणित और इतिहास में नकारात्मक सहप्रसरण (-24.44) है, जो दर्शाता है कि जो छात्र गणित में उच्च अंक प्राप्त करते हैं, वे इतिहास में कम अंक प्राप्त करते हैं। इसके विपरीत, जो छात्र गणित में कम अंक प्राप्त करते हैं वे इतिहास में उच्च अंक प्राप्त करते हैं।

चरण 4: सहप्रसरण मैट्रिक्स की कल्पना करें (वैकल्पिक)।

आप सीबॉर्न पैकेज के हीटमैप() फ़ंक्शन का उपयोग करके सहप्रसरण मैट्रिक्स की कल्पना कर सकते हैं:

 import seaborn as sns
import matplotlib.pyplot as plt

cov = np.cov(data, bias=True)
labs = ['math', 'science', 'history']

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs)
plt.show()

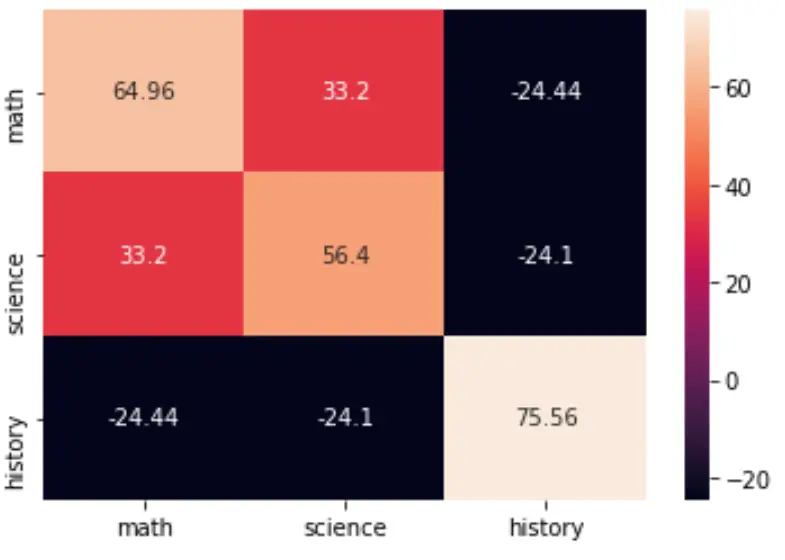
आप सीएमएपी तर्क निर्दिष्ट करके रंग पैलेट भी बदल सकते हैं:

 sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show() 

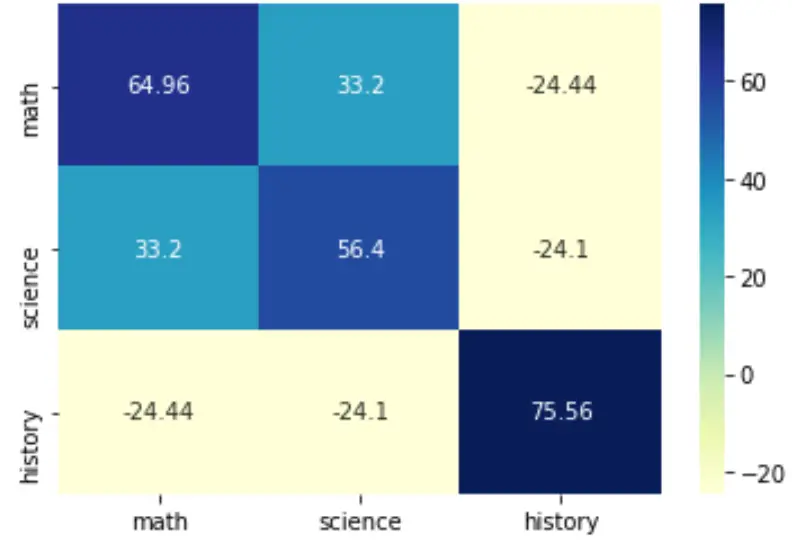
इस हीटमैप को स्टाइल करने के तरीके के बारे में अधिक जानकारी के लिए, सीबॉर्न दस्तावेज़ देखें।