सांख्यिकी में प्रायिकता द्रव्यमान फलन (पीएमएफ) क्या है?

एक संभाव्यता द्रव्यमान फ़ंक्शन , जिसे अक्सर संक्षिप्त रूप से पीएमएफ कहा जाता है, हमें संभावना बताता है कि एक अलग यादृच्छिक चर एक निश्चित मान लेता है।

उदाहरण के लिए, मान लीजिए कि हमने पासे को एक बार घुमाया। यदि हम x को उस संख्या को निरूपित करने देते हैं जिस पर पासा उतरता है, तो x के विभिन्न मानों के बराबर होने की संभावना को निम्नानुसार वर्णित किया जा सकता है:

• पी(एक्स=1): 1/6
• पी(एक्स=2): 1/6
• पी(एक्स=3): 1/6
• पी(एक्स=4): 1/6
• पी(एक्स=5): 1/6
• पी(एक्स=6): 1/6

इस बात की समान संभावना है कि पासा 1 और 6 के बीच किसी भी संख्या पर गिरेगा।

यहां बताया गया है कि हम इन संभावनाओं को संभाव्यता द्रव्यमान फ़ंक्शन के रूप में कैसे लिखेंगे:

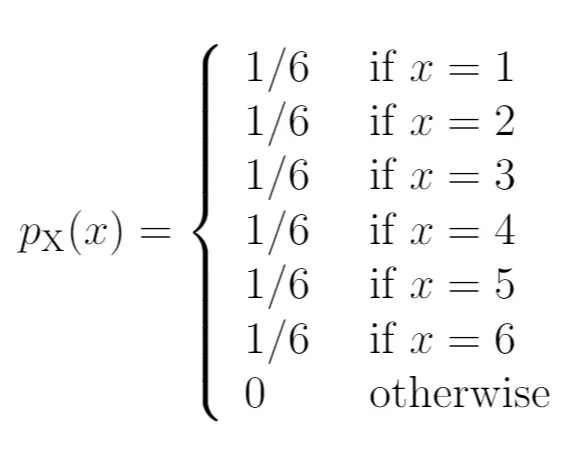
आरेख का बायां भाग दाहिनी ओर के परिणामों से जुड़ी संभाव्यता को दर्शाता है:

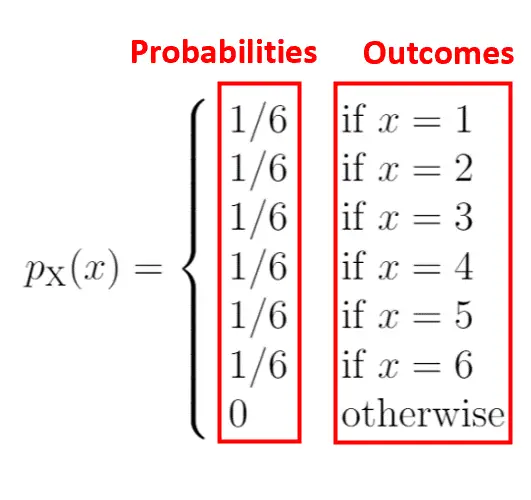
संभाव्यता द्रव्यमान फ़ंक्शन की एक विशेषता यह है कि सभी संभावनाओं का योग 1 होना चाहिए। आप देखेंगे कि यह पीएमएफ इस शर्त को पूरा करता है:

संभावनाओं का योग = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

संभाव्यता द्रव्यमान फ़ंक्शन के लिए समर्थन उन मानों के सेट को संदर्भित करता है जो असतत यादृच्छिक चर ले सकते हैं। इस उदाहरण में, समर्थन {1, 2, 3, 4, 5, 6} होगा क्योंकि पासे का मूल्य इनमें से कोई भी मान ले सकता है।

समर्थन के बाहर, पीएमएफ मूल्य शून्य है। उदाहरण के लिए, पासा “0” या “7” या “8” पर गिरने की संभावना शून्य है क्योंकि इनमें से कोई भी संख्या ब्रैकेट में शामिल नहीं है।

व्यवहार में संभाव्यता जन कार्य

व्यवहार में संभाव्यता द्रव्यमान कार्यों के दो सबसे आम उदाहरण द्विपद वितरण और पॉइसन वितरण से संबंधित हैं।

द्विपद वितरण

यदि एक यादृच्छिक चर X एक द्विपद वितरण का अनुसरण करता है, तो संभावना है कि X = k की सफलता निम्नलिखित सूत्र द्वारा पाई जा सकती है:

पी(एक्स=के) = _एन सी _के * पी ^के * (1-पी) ^एनके

सोना:

• n: परीक्षणों की संख्या
• k: सफलताओं की संख्या
• पी: किसी दिए गए परीक्षण पर सफलता की संभावना
• _n C _k : n परीक्षणों में k सफलताएँ प्राप्त करने के तरीकों की संख्या

उदाहरण के लिए, मान लीजिए कि हम एक सिक्के को 3 बार उछालते हैं। हम इन 3 उछालों पर 0, 1, 2 और 3 चित आने की संभावना निर्धारित करने के लिए उपरोक्त सूत्र का उपयोग कर सकते हैं:

• पी(एक्स=0) = ₃ सी ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125
• पी(एक्स=1) = ₃ सी ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 1 * 1 * (0.5) ² = 0.375
• पी(एक्स=2) = ₃ सी ₂ * 0.5 ² * (1-0.5) ^3-2 = 1 * 1 * (0.5) ¹ = 0.375
• पी(एक्स=3) = ₃ सी ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 1 * (0.5) ⁰ = 0.125

मछली वितरण

यदि एक यादृच्छिक चर

पी(एक्स=के) = λ ^के * ई ^{– λ} / के!

सोना:

• λ: एक विशिष्ट अंतराल के दौरान होने वाली सफलताओं की औसत संख्या
• k: सफलताओं की संख्या
• ई: लगभग 2.71828 के बराबर एक स्थिरांक

उदाहरण के लिए, मान लीजिए कि किसी विशेष अस्पताल में प्रति घंटे औसतन 2 जन्म होते हैं। हम 0, 1, 2, 3 जन्म आदि का अनुभव करने की संभावना निर्धारित करने के लिए उपरोक्त सूत्र का उपयोग कर सकते हैं। किसी दिए गए घंटे में:

• पी(एक्स=0) = 2 ⁰ * ई ^{– 2} / 0! = 0.1353
• पी(एक्स=1) = 2 ¹ * ई ^{– 2/1} ! = 0.2707
• पी(एक्स=2) = 2 ² * ई ^{– 2/2} ! = 0.2707
• पी(एक्स=3) = 2 ³ * ई ^-2 /3! = 0.1805

एक पीएमएफ देखें

हम अक्सर बार ग्राफ़ के साथ संभाव्यता द्रव्यमान कार्यों की कल्पना करते हैं।

उदाहरण के लिए, निम्नलिखित बार चार्ट पिछले उदाहरण में वर्णित पॉइसन वितरण के लिए प्रति घंटे जन्मों की संख्या से जुड़ी संभावनाओं को दर्शाता है:

ध्यान दें कि जन्मों की संख्या अनंत तक बढ़ सकती है, लेकिन संभावनाएँ 10 के बाद इतनी छोटी हो जाती हैं कि आप उन्हें बार ग्राफ़ पर भी नहीं देख सकते हैं।

पीएमएफ के गुण

संभाव्यता द्रव्यमान फलन में निम्नलिखित गुण होते हैं:

1. समर्थन में सभी संभावनाएँ सकारात्मक हैं। उदाहरण के लिए, 1 और 6 के बीच पासे के गिरने की संभावना सकारात्मक है, जबकि अन्य सभी परिणामों की संभावना शून्य है।

2. सभी परिणामों की संभावना 0 और 1 के बीच होती है। उदाहरण के लिए, 1 और 6 के बीच पासे के गिरने की संभावना 1/6 है, या प्रत्येक परिणाम के लिए 0.1666666 है।

3. सभी संभावनाओं का योग 1 के बराबर होना चाहिए। उदाहरण के लिए, एक निश्चित संख्या पर गिरने वाले पासे की संभावनाओं का योग 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1 है। /6 = 1.

अतिरिक्त संसाधन

यादृच्छिक चर क्या हैं?
सीडीएफ या पीडीएफ: क्या अंतर है?
द्विपद वितरण का परिचय
पॉइसन वितरण का परिचय