मशीन लर्निंग में पूर्वाग्रह-विचरण ट्रेडऑफ़ क्या है?

डेटा सेट पर किसी मॉडल के प्रदर्शन का मूल्यांकन करने के लिए, हमें यह मापने की आवश्यकता है कि मॉडल की भविष्यवाणियां देखे गए डेटा से कितनी अच्छी तरह मेल खाती हैं।

प्रतिगमन मॉडल के लिए, सबसे अधिक इस्तेमाल किया जाने वाला मीट्रिक माध्य वर्ग त्रुटि (MSE) है, जिसकी गणना निम्नानुसार की जाती है:

एमएसई = (1/एन)*Σ(वाई _आई – एफ(एक्स _आई )) ²

सोना:

• n: अवलोकनों की कुल संख्या
• y _i : ^iवें अवलोकन का प्रतिक्रिया मूल्य
• f(x _i ): i ^वें अवलोकन का अनुमानित प्रतिक्रिया मूल्य

मॉडल की भविष्यवाणियां अवलोकनों के जितनी करीब होंगी, एमएसई उतना ही कम होगा।

हालाँकि, हम केवल एमएसई परीक्षण – एमएसई की परवाह करते हैं जब हमारा मॉडल अनदेखे डेटा पर लागू होता है। ऐसा इसलिए है क्योंकि हम केवल इस बात की परवाह करते हैं कि मॉडल अज्ञात डेटा पर कैसा प्रदर्शन करेगा, मौजूदा डेटा पर नहीं।

उदाहरण के लिए, यह ठीक है अगर स्टॉक की कीमतों की भविष्यवाणी करने वाले मॉडल में ऐतिहासिक डेटा पर कम एमएसई है, लेकिन हम वास्तव में भविष्य के डेटा की सटीक भविष्यवाणी करने के लिए मॉडल का उपयोग करने में सक्षम होना चाहते हैं।

यह पता चला है कि एमएसई परीक्षण को अभी भी दो भागों में विभाजित किया जा सकता है:

(1) वेरिएंस: यह संदर्भित करता है कि यदि हम एक अलग प्रशिक्षण सेट का उपयोग करके इसका अनुमान लगाते हैं तो हमारा फ़ंक्शन f कितना बदल जाएगा।

(2) पूर्वाग्रह: एक वास्तविक समस्या का सामना करने से उत्पन्न त्रुटि को संदर्भित करता है, जो कि बहुत सरल मॉडल के साथ बेहद जटिल हो सकती है।

गणितीय शब्दों में लिखा गया:

एमएसई परीक्षण = वार( एफ̂( x ₀ )) + [पूर्वाग्रह( एफ̂( x ₀ ))] ² + वार(ε)

एमएसई परीक्षण = वेरिएंस + बायस ² + इरेड्यूसबल त्रुटि

तीसरा पद, इरेड्यूसेबल त्रुटि, वह त्रुटि है जिसे किसी भी मॉडल द्वारा केवल इसलिए कम नहीं किया जा सकता क्योंकि व्याख्यात्मक चर के सेट और प्रतिक्रिया चर के बीच संबंध में हमेशा शोर होता है।

जिन मॉडलों में पूर्वाग्रह अधिक होता है उनमें विचरण कम होता है । उदाहरण के लिए, रैखिक प्रतिगमन मॉडल में उच्च पूर्वाग्रह (व्याख्यात्मक चर और प्रतिक्रिया चर के बीच एक सरल रैखिक संबंध मानते हुए) और कम विचरण होता है (मॉडल का अनुमान नमूना से नमूना में ज्यादा नहीं बदलेगा)। अन्य)।

हालाँकि, कम पूर्वाग्रह वाले मॉडल में उच्च भिन्नता होती है। उदाहरण के लिए, जटिल नॉनलाइनियर मॉडल में कम पूर्वाग्रह होते हैं (व्याख्यात्मक चर और प्रतिक्रिया चर के बीच एक निश्चित संबंध नहीं मानते हैं) उच्च विचरण के साथ (मॉडल अनुमान सीखने के एक नमूने से दूसरे में महत्वपूर्ण रूप से बदल सकते हैं)।

पूर्वाग्रह-विचरण व्यापार-बंद

पूर्वाग्रह-विचरण व्यापार-बंद उस व्यापार-बंद को संदर्भित करता है जो तब होता है जब हम पूर्वाग्रह को कम करना चुनते हैं, जो आम तौर पर भिन्नता को बढ़ाता है, या भिन्नता को कम करने के लिए चुनता है, जो आम तौर पर पूर्वाग्रह को बढ़ाता है।

निम्नलिखित ग्राफ़ इस व्यापार-बंद की कल्पना करने का एक तरीका प्रदान करता है:

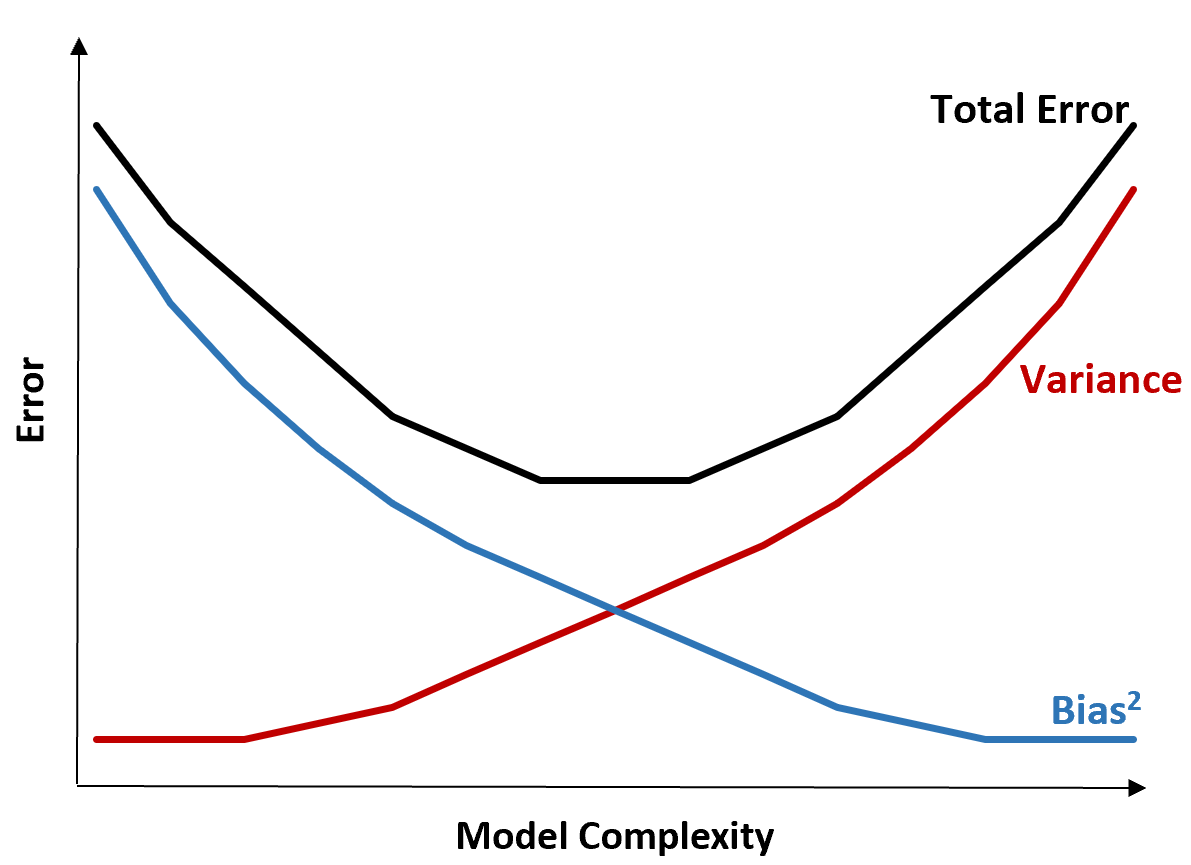
किसी मॉडल की जटिलता बढ़ने पर कुल त्रुटि कम हो जाती है, लेकिन केवल एक निश्चित बिंदु तक। एक निश्चित बिंदु के बाद, विचरण बढ़ने लगता है और कुल त्रुटि भी बढ़ने लगती है।

व्यवहार में, हम केवल मॉडल की कुल त्रुटि को कम करने की परवाह करते हैं, जरूरी नहीं कि भिन्नता या पूर्वाग्रह को कम करें। यह पता चला है कि कुल त्रुटि को कम करने का तरीका भिन्नता और पूर्वाग्रह के बीच सही संतुलन ढूंढना है।

दूसरे शब्दों में, हम एक मॉडल जटिल चाहते हैं जो व्याख्यात्मक चर और प्रतिक्रिया चर के बीच वास्तविक संबंध को पकड़ सके, लेकिन इतना जटिल नहीं कि उन पैटर्न का पता लगा सके जो वास्तव में मौजूद नहीं हैं।

जब कोई मॉडल बहुत जटिल होता है, तो यह डेटा पर हावी हो जाता है । ऐसा इसलिए होता है क्योंकि प्रशिक्षण डेटा में ऐसे पैटर्न ढूंढना बहुत मुश्किल होता है जो केवल संयोग से उत्पन्न होते हैं। इस प्रकार के मॉडल के अदृश्य डेटा पर खराब प्रदर्शन करने की संभावना है।

लेकिन जब कोई मॉडल बहुत सरल होता है, तो वह डेटा को कम आंकता है । ऐसा इसलिए होता है क्योंकि यह माना जाता है कि व्याख्यात्मक चर और प्रतिक्रिया चर के बीच वास्तविक संबंध वास्तव में जितना सरल है उससे कहीं अधिक सरल है।

मशीन लर्निंग में इष्टतम मॉडल का चयन करने का तरीका भविष्य में अनदेखे डेटा पर मॉडल के परीक्षण की त्रुटि को कम करने के लिए पूर्वाग्रह और भिन्नता के बीच संतुलन ढूंढना है।

व्यवहार में, परीक्षणों के एमएसई को कम करने का सबसे आम तरीका क्रॉस-सत्यापन का उपयोग करना है।