पृथक समान वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि असतत समान वितरण क्या है और इसका विशिष्ट सूत्र क्या है। इसी तरह, आप असतत समान वितरण का चित्रमय प्रतिनिधित्व और इसके गुण क्या हैं, देख पाएंगे।

असतत समान वितरण क्या है?

असतत समान वितरण एक असतत संभाव्यता वितरण है जिसमें सभी मान समसंभाव्य होते हैं, अर्थात असतत समान वितरण में सभी मूल्यों के घटित होने की संभावना समान होती है।

उदाहरण के लिए, पासे के रोल को एक अलग समान वितरण के साथ परिभाषित किया जा सकता है, क्योंकि सभी संभावित परिणामों (1, 2, 3, 4, 5, या 6) के घटित होने की संभावना समान है।

सामान्य तौर पर, एक असतत समान वितरण में दो विशिष्ट पैरामीटर होते हैं, ए और बी , जो वितरण द्वारा लिए जा सकने वाले संभावित मानों की सीमा को परिभाषित करते हैं। इस प्रकार, जब एक चर को असतत समान वितरण द्वारा परिभाषित किया जाता है, तो इसे Uniform(a,b) लिखा जाता है।

असतत समान वितरण का उपयोग यादृच्छिक प्रयोगों का वर्णन करने के लिए किया जा सकता है क्योंकि यदि सभी परिणामों की संभावना समान है, तो इसका मतलब है कि प्रयोग यादृच्छिक है।

असतत समान वितरण सूत्र

अब जब हम असतत समान वितरण की परिभाषा जानते हैं, तो हम देखेंगे कि वह कौन सा सूत्र है जो हमें इस प्रकार के वितरण के मूल्यों की उपस्थिति की संभावना की गणना करने की अनुमति देता है।

असतत समान वितरण का संभाव्यता फलन स्थिर होता है और इसका मान संभावित परिणामों की कुल संख्या के एक के बराबर होता है। इस प्रकार, असतत समान वितरण का सूत्र इस प्रकार है:

$P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}$

दूसरी ओर, असतत समान वितरण के संचयी संभाव्यता फ़ंक्शन का सूत्र इस प्रकार है:

$P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}$

सोना

$a$

और

$b$

असतत समान वितरण के विशिष्ट पैरामीटर हैं।

असतत समान वितरण आरेख

चूँकि असतत समान वितरण एक अंतराल में केवल कुछ मान ले सकता है, इसके ग्राफिकल प्रतिनिधित्व में बिंदु होते हैं। इसके अलावा, सभी संभावनाएँ समान हैं, इसलिए असतत समान वितरण में सभी बिंदुओं का ऊर्ध्वाधर समन्वय समान है।

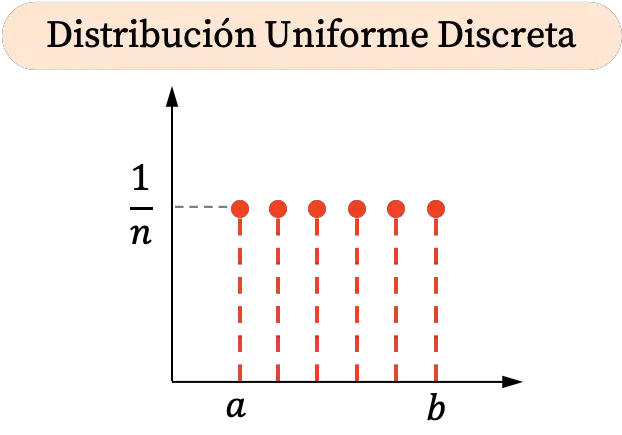
दूसरी ओर, असतत समान वितरण का संचयी संभाव्यता ग्राफ इस प्रकार है:

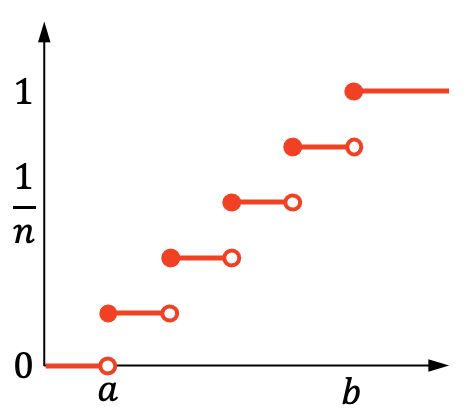
असतत समान वितरण के लक्षण

असतत समान वितरण में निम्नलिखित विशेषताएं हैं:

असतत समान वितरण को दो पूर्णांक मापदंडों, ए और बी द्वारा परिभाषित किया गया है, जो वितरण के संभावित मूल्यों की सीमा निर्धारित करते हैं।

$\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}$

एक असतत समान वितरण का माध्य इसके दो विशिष्ट मापदंडों के योग को दो से विभाजित करने के बराबर होता है।

$E[X]=\cfrac{a+b}{2}$

एक असतत समान वितरण का माध्य उसके माध्य के बराबर होता है, इसलिए इसकी गणना उसी अभिव्यक्ति के साथ की जाती है:

$Me=\cfrac{a+b}{2}$

एक असतत समान वितरण का प्रसरण परिणामों की कुल संख्या के वर्ग के बराबर होता है जिसमें से एक को बारह से विभाजित किया जाता है।

$Var(X)=\cfrac{n^2-1}{12}$

असतत समान वितरण अपने माध्य के बारे में सममित है, इसलिए, इस संभाव्यता वितरण का तिरछापन गुणांक शून्य है।

$A=0$

असतत समान वितरण के कुर्टोसिस की गणना निम्नलिखित अभिव्यक्ति का उपयोग करके की जा सकती है:

$C=-\cfrac{6\cdot (n^2+1)}{5\cdot (n^2+1)}$

असतत समान वितरण और सतत समान वितरण

अंत में, हम देखेंगे कि असतत समान वितरण और सतत समान वितरण के बीच क्या अंतर है, क्योंकि वे दो समान प्रकार के संभाव्यता वितरण हैं लेकिन पर्याप्त अंतर के साथ।

असतत समान वितरण और सतत समान वितरण के बीच का अंतर उनके संभावित मूल्यों में निहित है। असतत समान वितरण एक अंतराल में केवल कुछ मान ले सकता है, जबकि निरंतर समान वितरण उस अंतराल में कोई भी मान ले सकता है जिसमें इसे परिभाषित किया गया है।

सामान्य तौर पर, असतत समान वितरण केवल पूर्णांक मान ले सकते हैं, जबकि निरंतर समान वितरण दशमलव मान भी ले सकते हैं।

➤ देखें: सतत एक समान वितरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने