फी गुणांक: परिभाषा और उदाहरण

फाई गुणांक (कभी-कभी माध्य वर्ग आकस्मिकता गुणांक कहा जाता है) दो बाइनरी चर के बीच संबंध का एक माप है।

दो यादृच्छिक चर x और y के लिए दी गई 2×2 तालिका के लिए:

फाई गुणांक की गणना निम्नानुसार की जा सकती है:

Φ = (एडी-बीसी) / √ (ए+बी)(सी+डी)(ए+सी)(बी+डी)

उदाहरण: फाई गुणांक की गणना

मान लीजिए हम जानना चाहते हैं कि किसी राजनीतिक दल की प्राथमिकता के साथ लिंग का संबंध है या नहीं। हम 25 मतदाताओं का एक सरल यादृच्छिक नमूना लेते हैं और उनसे उनकी राजनीतिक पार्टी की पसंद के बारे में पूछते हैं। निम्नलिखित तालिका सर्वेक्षण के परिणाम प्रस्तुत करती है:

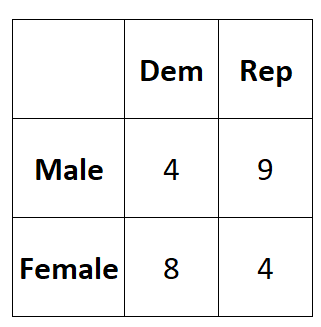
हम दो चरों के बीच Phi गुणांक की गणना निम्नानुसार कर सकते हैं:

Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0.3589

नोट: हम इसकी गणना Phi गुणांक कैलकुलेटर का उपयोग करके भी कर सकते थे।

फाई गुणांक की व्याख्या कैसे करें

पियर्सन सहसंबंध गुणांक के समान, फाई गुणांक -1 और 1 के बीच मान लेता है जहां:

• -1 दो चरों के बीच पूर्णतया नकारात्मक संबंध दर्शाता है।
• 0 दो चरों के बीच कोई संबंध नहीं दर्शाता है।
• 1 दो चरों के बीच पूर्णतः सकारात्मक संबंध दर्शाता है।

सामान्य तौर पर, Phi गुणांक शून्य से जितना अधिक होता है, दोनों चर के बीच संबंध उतना ही मजबूत होता है।

दूसरे शब्दों में, Phi गुणांक शून्य से जितना दूर होगा, दोनों चरों के बीच किसी प्रकार के व्यवस्थित पैटर्न का उतना ही अधिक प्रमाण होगा।

अतिरिक्त संसाधन

पियर्सन सहसंबंध गुणांक के लिए एक गाइड
फिशर सटीक परीक्षण के लिए एक गाइड
स्वतंत्रता के ची-स्क्वायर परीक्षण के लिए एक गाइड